用.NET模擬天體運動

這將是一篇罕見而偏極客的文章。

我上大學時就見過一些模擬太陽系等天體運動的軟體和網站，覺得非常酷炫，比如這個（http://www.astronoo.com/en/articles/positions-of-the-planets.html）：

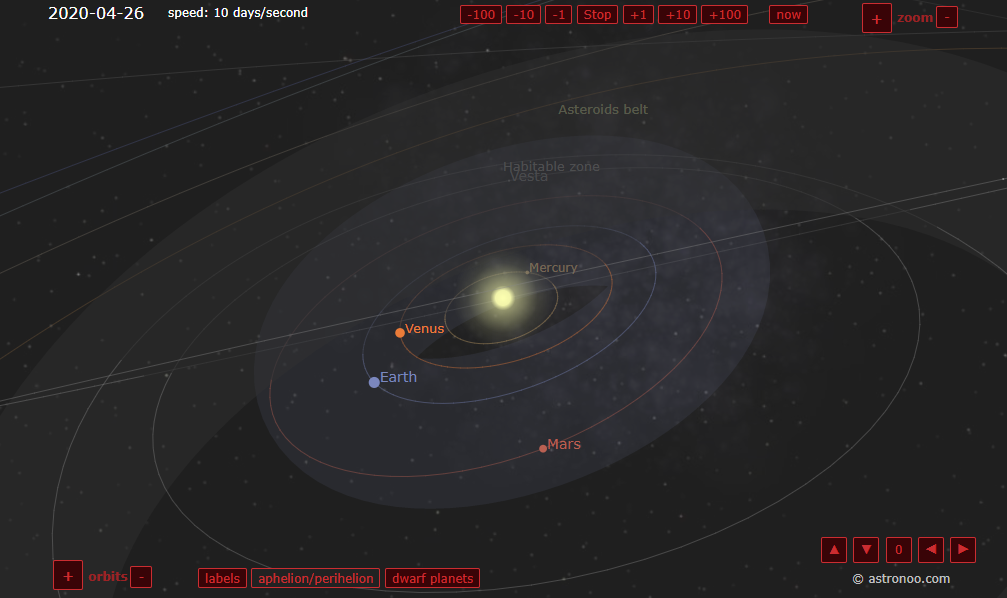
其酷炫之處不僅在於天體運動軌跡能畫出美妙的弧線，更重要的是其運動規律完全由萬有引力定律產生，不需要對其運動軌跡進行程式設計。所有天體受其它天體的合力，然後按照其加速度執行。只需一個起始座標和起始速度，就能坐下來欣賞畫面。

我從大學畢業後就一直對這個抱有深厚興趣，工作第一年時我就用C++做過一版；後來我負責公司前端工作，又用js/canvas

需要的數學知識

由於是程式看數學知識，此處我將使用程式碼來表示公式。

• 萬有引力，該力F與兩個天體的質量m1, m2成正比，如距離r的平方成反比，用程式碼表示為：F = m1 * m2 * G / r ^ 2；
• 牛頓第二定律，加速度a等於合力F除以質量m，用程式碼表示為：a = F / m；
• 速度v與加速度a以及時間t的關係，用程式碼表示為：v = a * t；
• 距離s與速度v以及時間t的關係，用程式碼表示為：s = v * t。

這裡面的所有知識都已經在高中物理提過了，但有兩點需要注意：

• 所有的力、加速度、速度以及距離都需要分為x
  軸和y軸兩個分量；
• 所有的時間t實際上是小段時間dt，程式將迴圈模擬小段時間累加起來，來模擬天體運動。

核心程式碼

天體類：

class Star
{
    public LinkedList<Vector2> PositionTrack = new LinkedList<SharpDX.Vector2>();
    public double Px, Py, Vx, Vy;
    public double Mass;
    public float Size => (float)Math.Log(Mass) * 2;
    public Color Color = Color.Black;
    
    public void Move(double step)
    {
        Px += Vx * step;
        Py += Vy * step;
        PositionTrack.AddFirst(new Vector2((float)Px, (float)Py));
        if (PositionTrack.Count > 1000)
        {
            PositionTrack.RemoveLast();
        }
    }
}
 

注意，我沒指定大小Size，直接給值為其質量的對數乘2，另外注意我使用了一個PositionTrack的連結串列來儲存其運動軌跡。

萬有引力、加速度、速度計算

void Step()
{
    foreach (var s1 in Stars)
    {
        // star velocity
        // F = G * m1 * m2 / r^2
        // F has a direction: 
        double Fdx = 0;
        double Fdy = 0;

        const double Gm1 = 100.0f;     // G*s1.m
        var ttm = StepDt * StepDt; // t*t/s1.m

        foreach (var s2 in Stars)
        {
            if (s1 == s2) continue;

            var rx = s2.Px - s1.Px;
            var ry = s2.Py - s1.Py;
            var rr = rx * rx + ry * ry;
            var r = Math.Sqrt(rr);

            var f = Gm1 * s2.Mass / rr;
            var fdx = f * rx / r;
            var fdy = f * ry / r;

            Fdx += fdx;
            Fdy += fdy;
        }

        // Ft = ma  -> a = Ft/m
        // v  = at  -> v = Ftt/m
        var dvx = Fdx * ttm;
        var dvy = Fdy * ttm;
        s1.Vx += dvx;
        s1.Vy += dvy;
    }

    foreach (var star in Stars)
    {
        star.Move(StepDt);
    }
}

注意其中有個foreach迴圈，它將一一計算每個天體對某天體的力，然後通過累加的方式求出合力，最後依照合力計算加速度和速度。如果使用gmp等高精度計算庫，該迴圈將存在效能熱點，因此可以將這個foreach改成Parallel.For加lock的方式修改合力Fdx和Fdy，可以提高效能（C++的程式碼就是這樣寫的）。

繪圖程式碼

public void Draw(DeviceContext ctx)
{
    ctx.Clear(Color.DarkGray);
    
    using var solidBrash = new SolidColorBrush(ctx, Color.White);

    float allHeight = ctx.Size.Height;
    float allWidth = ctx.Size.Width;
    float scale = allHeight / 100.0f;
    foreach (var star in Stars)
    {
        using var radialBrush = new RadialGradientBrush(ctx, new RadialGradientBrushProperties
        {
            Center = Vector2.Zero,
            RadiusX = 1.0f,
            RadiusY = 1.0f,
        }, new SharpDX.Direct2D1.GradientStopCollection(ctx, new[]
        {
            new GradientStop{ Color = Color.White, Position = 0f},
            new GradientStop{ Color = star.Color, Position = 1.0f},
        }));

        ctx.Transform =
            Matrix3x2.Scaling(star.Size) *
            Matrix3x2.Translation(((float)star.Px + 50) * scale + (allWidth - allHeight) / 2, ((float)star.Py + 50) * scale);
        ctx.FillEllipse(new Ellipse(Vector2.Zero, 1, 1), radialBrush);

        ctx.Transform =
            Matrix3x2.Translation(allHeight / 2 + (allWidth - allHeight) / 2, allHeight / 2);
        foreach (var line in star.PositionTrack.Zip(star.PositionTrack.Skip(1)))
        {
            ctx.DrawLine(line.First * scale, line.Second * scale, solidBrash, 1.0f);
        }
    }
    ctx.Transform = Matrix3x2.Identity;
}

注意我在繪圖程式碼邏輯中做了一些矩陣變換，我把所有邏輯做成了窗體解析度無關的，假定螢幕長和寬的較小值為100，然後左上角座標為-50, -50，右下角座標為50, 50。

星系模擬

太陽、地球和月亮

這是最容易想到了，地球繞太陽轉，月亮繞地球轉，建立程式碼如下：

public static StarSystem CreateSolarEarthMoon()
{
    var solar = new Star
    {
        Px = 0, Py = 0,
        Vx = 0.6, Vy = 0,
        Mass = 1000,
        Color = Color.Red,
    };

    // Earth
    var earth = new Star
    {
        Px = 0, Py = -41,
        Vx = -5, Vy = 0,
        Mass = 100,
        Color = Color.Blue,
    };

    // Moon
    var moon = new Star
    {
        Px = 0, Py = -45,
        Vx = -10, Vy = 0,
        Mass = 10,
    };

    return new StarSystem(new List<Star> { solar, earth, moon });
}

注意所有資料都沒使用真實數字模擬（不然地球繞太陽轉一圈需要365天才能看完