神經網路系列之三 -- 損失函式
系列部落格,原文在筆者所維護的github上:https://aka.ms/beginnerAI,
點選star加星不要吝嗇,星越多筆者越努力。
第3章 損失函式
3.0 損失函式概論
3.0.1 概念
在各種材料中經常看到的中英文詞彙有:誤差,偏差,Error,Cost,Loss,損失,代價......意思都差不多,在本書中,使用“損失函式”和“Loss Function”這兩個詞彙,具體的損失函式符號用J來表示,誤差值用loss表示。
“損失”就是所有樣本的“誤差”的總和,亦即(m為樣本數):
\[損失 = \sum^m_{i=1}誤差_i\]
\[J = \sum_{i=1}^m loss\]
在黑盒子的例子中,我們如果說“某個樣本的損失”是不對的,只能說“某個樣本的誤差”,因為樣本是一個一個計算的。如果我們把神經網路的引數調整到完全滿足獨立樣本的輸出誤差為0,通常會令其它樣本的誤差變得更大,這樣作為誤差之和的損失函式值,就會變得更大。所以,我們通常會在根據某個樣本的誤差調整權重後,計算一下整體樣本的損失函式值,來判定網路是不是已經訓練到了可接受的狀態。
損失函式的作用
損失函式的作用,就是計算神經網路每次迭代的前向計算結果與真實值的差距,從而指導下一步的訓練向正確的方向進行。
如何使用損失函式呢?具體步驟:
- 用隨機值初始化前向計算公式的引數;
- 代入樣本,計算輸出的預測值;
- 用損失函式計算預測值和標籤值(真實值)的誤差;
- 根據損失函式的導數,沿梯度最小方向將誤差回傳,修正前向計算公式中的各個權重值;
- goto 2, 直到損失函式值達到一個滿意的值就停止迭代。
3.0.2 機器學習常用損失函式
符號規則:a是預測值,y是樣本標籤值,J是損失函式值。
Gold Standard Loss,又稱0-1誤差
\[ loss=\begin{cases} 0 & a=y \\ 1 & a \ne y \end{cases} \]絕對值損失函式
\[ loss = |y-a| \]
- Hinge Loss,鉸鏈/摺頁損失函式或最大邊界損失函式,主要用於SVM(支援向量機)中
\[ loss=max(0,1-y \cdot a), y=\pm 1 \]
- Log Loss,對數損失函式,又叫交叉熵損失函式(cross entropy error)
\[ loss = -\frac{1}{m} \sum_i^m y_i log(a_i) + (1-y_i)log(1-a_i) \qquad y_i \in \{0,1\} \]
Squared Loss,均方差損失函式
\[ loss=\frac{1}{2m} \sum_i^m (a_i-y_i)^2 \]Exponential Loss,指數損失函式
\[ loss = \frac{1}{m}\sum_i^m e^{-(y_i \cdot a_i)} \]
3.0.3 損失函式影象理解
用二維函式影象理解單變數對損失函式的影響
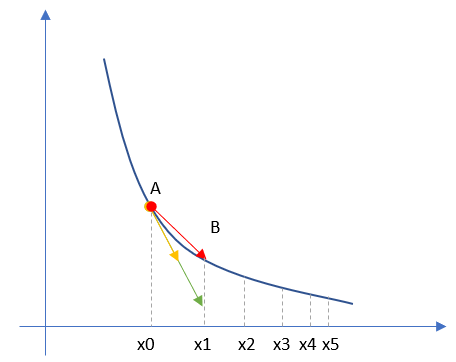
圖3-1 單變數的損失函式圖
圖3-1中,縱座標是損失函式值,橫座標是變數。不斷地改變變數的值,會造成損失函式值的上升或下降。而梯度下降演算法會讓我們沿著損失函式值下降的方向前進。
- 假設我們的初始位置在A點,\(x=x0\),損失函式值(縱座標)較大,回傳給網路做訓練;
- 經過一次迭代後,我們移動到了B點,\(x=x1\),損失函式值也相應減小,再次回傳重新訓練;
- 以此節奏不斷向損失函式的最低點靠近,經歷了\(x2、x3、x4、x5\);
- 直到損失值達到可接受的程度,比如\(x5\)的位置,就停止訓練。
用等高線圖理解雙變數對損失函式影響
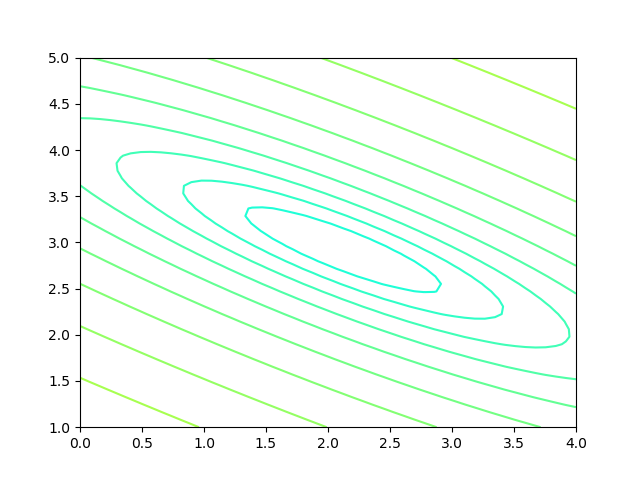
圖3-2 雙變數的損失函式圖
圖3-2中,橫座標是一個變數\(w\),縱座標是另一個變數\(b\)。兩個變數的組合形成的損失函式值,在圖中對應處於等高線上的唯一的一個座標點。\(w、b\)所有的不同的值的組合會形成一個損失函式值的矩陣,我們把矩陣中具有相同(相近)損失函式值的點連線起來,可以形成一個不規則橢圓,其圓心位置,是損失值為0的位置,也是我們要逼近的目標。
這個橢圓如同平面地圖的等高線,來表示的一個窪地,中心位置比邊緣位置要低,通過對損失函式值的計算,對損失函式的求導,會帶領我們沿著等高線形成的梯子一步步下降,無限逼近中心點。
3.0.4 神經網路中常用的損失函式
均方差函式,主要用於迴歸
交叉熵函式,主要用於分類
二者都是非負函式,極值在底部,用梯度下降法可以求解。
系列部落格,原文在筆者所維護的github上:https://aka.ms/beginnerAI,
點選star加星不要吝嗇,星越多筆者越努力。
3.1 均方差函式
MSE - Mean Square Error。
該函式就是最直觀的一個損失函數了,計算預測值和真實值之間的歐式距離。預測值和真實值越接近,兩者的均方差就越小。
均方差函式常用於線性迴歸(linear regression),即函式擬合(function fitting)。公式如下:
\[ loss = {1 \over 2}(z-y)^2 \tag{單樣本} \]
\[ J=\frac{1}{2m} \sum_{i=1}^m (z_i-y_i)^2 \tag{多樣本} \]
3.1.1 工作原理
要想得到預測值a與真實值y的差距,最樸素的想法就是用\(Error=a_i-y_i\)。
對於單個樣本來說,這樣做沒問題,但是多個樣本累計時,\(a_i-y_i\)有可能有正有負,誤差求和時就會導致相互抵消,從而失去價值。所以有了絕對值差的想法,即\(Error=|a_i-y_i|\)。這看上去很簡單,並且也很理想,那為什麼還要引入均方差損失函式呢?兩種損失函式的比較如表3-1所示。
表3-1 絕對值損失函式與均方差損失函式的比較
| 樣本標籤值 | 樣本預測值 | 絕對值損失函式 | 均方差損失函式 |
|---|---|---|---|
| \([1,1,1]\) | \([1,2,3]\) | \((1-1)+(2-1)+(3-1)=3\) | \((1-1)^2+(2-1)^2+(3-1)^2=5\) |
| \([1,1,1]\) | \([1,3,3]\) | \((1-1)+(3-1)+(3-1)=4\) | \((1-1)^2+(3-1)^2+(3-1)^2=8\) |
| \(4/3=1.33\) | \(8/5=1.6\) |
可以看到5比3已經大了很多,8比4大了一倍,而8比5也放大了某個樣本的區域性損失對全域性帶來的影響,用術語說,就是“對某些偏離大的樣本比較敏感”,從而引起監督訓練過程的足夠重視,以便回傳誤差。
3.1.2 實際案例
假設有一組資料如圖3-3,我們想找到一條擬合的直線。
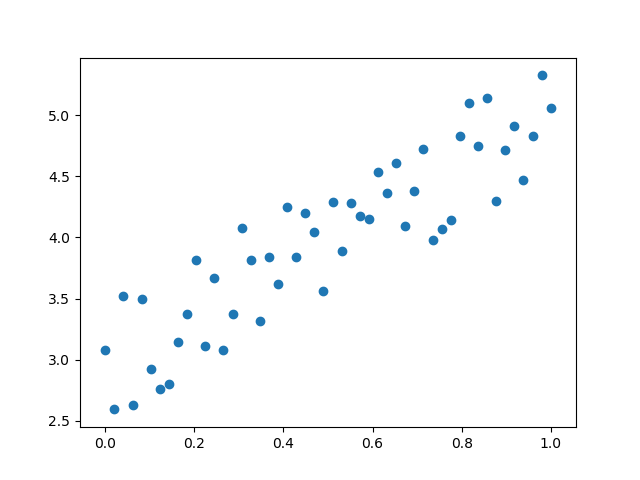
圖3-3 平面上的樣本資料
圖3-4中,前三張顯示了一個逐漸找到最佳擬合直線的過程。
- 第一張,用均方差函式計算得到Loss=0.53;
- 第二張,直線向上平移一些,誤差計算Loss=0.16,比圖一的誤差小很多;
- 第三張,又向上平移了一些,誤差計算Loss=0.048,此後還可以繼續嘗試平移(改變b值)或者變換角度(改變w值),得到更小的損失函式值;
- 第四張,偏離了最佳位置,誤差值Loss=0.18,這種情況,演算法會讓嘗試方向反向向下。
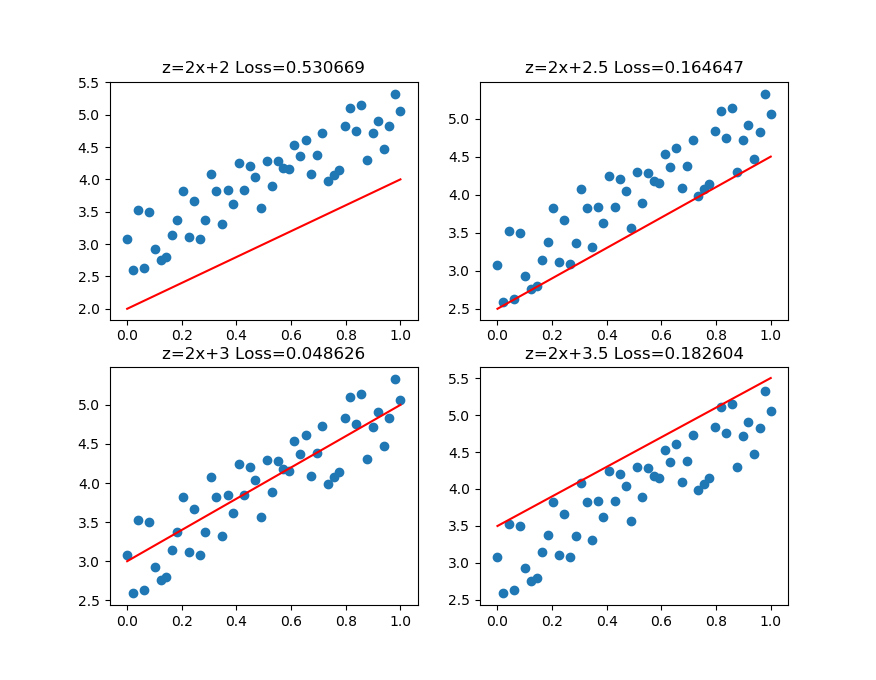
圖3-4 損失函式值與直線位置的關係
第三張圖損失函式值最小的情況。比較第二張和第四張圖,由於均方差的損失函式值都是正值,如何判斷是向上移動還是向下移動呢?
在實際的訓練過程中,是沒有必要計算損失函式值的,因為損失函式值會體現在反向傳播的過程中。我們來看看均方差函式的導數:
\[ \frac{\partial{J}}{\partial{a_i}} = a_i-y_i \]
雖然\((a_i-y_i)^2\)永遠是正數,但是\(a_i-y_i\)卻可以是正數(直線在點下方時)或者負數(直線在點上方時),這個正數或者負數被反向傳播回到前面的計算過程中,就會引導訓練過程朝正確的方向嘗試。
在上面的例子中,我們有兩個變數,一個w,一個b,這兩個值的變化都會影響最終的損失函式值的。
我們假設該擬合直線的方程是y=2x+3,當我們固定w=2,把b值從2到4變化時,看看損失函式值的變化如圖3-5所示。

圖3-5 固定W時,b的變化造成的損失值
我們假設該擬合直線的方程是y=2x+3,當我們固定b=3,把w值從1到3變化時,看看損失函式值的變化如圖3-6所示。
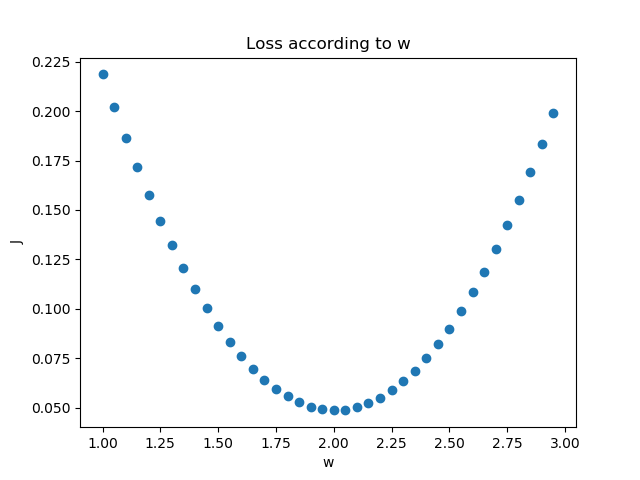
圖3-6 固定b時,W的變化造成的損失值
3.1.3 損失函式的視覺化
損失函式值的3D示意圖
橫座標為W,縱座標為b,針對每一個w和一個b的組合計算出一個損失函式值,用三維圖的高度來表示這個損失函式值。下圖中的底部並非一個平面,而是一個有些下凹的曲面,只不過曲率較小,如圖3-7。
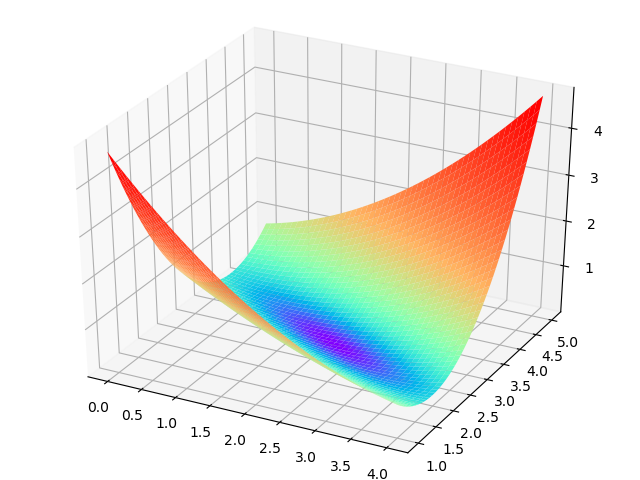
圖3-7 W和b同時變化時的損失值形成的曲面
損失函式值的2D示意圖
在平面地圖中,我們經常會看到用等高線的方式來表示海拔高度值,下圖就是上圖在平面上的投影,即損失函式值的等高線圖,如圖3-8所示。

圖3-8 損失函式的等高線圖
如果還不能理解的話,我們用最笨的方法來畫一張圖,程式碼如下:
s = 200
W = np.linspace(w-2,w+2,s)
B = np.linspace(b-2,b+2,s)
LOSS = np.zeros((s,s))
for i in range(len(W)):
for j in range(len(B)):
z = W[i] * x + B[j]
loss = CostFunction(x,y,z,m)
LOSS[i,j] = round(loss, 2)上述程式碼針對每個w和b的組合計算出了一個損失值,保留小數點後2位,放在LOSS矩陣中,如下所示:
[[4.69 4.63 4.57 ... 0.72 0.74 0.76]
[4.66 4.6 4.54 ... 0.73 0.75 0.77]
[4.62 4.56 4.5 ... 0.73 0.75 0.77]
...
[0.7 0.68 0.66 ... 4.57 4.63 4.69]
[0.69 0.67 0.65 ... 4.6 4.66 4.72]
[0.68 0.66 0.64 ... 4.63 4.69 4.75]]然後遍歷矩陣中的損失函式值,在具有相同值的位置上繪製相同顏色的點,比如,把所有值為0.72的點繪製成紅色,把所有值為0.75的點繪製成藍色......,這樣就可以得到圖3-9。

圖3-9 用笨辦法繪製等高線圖
此圖和等高線圖的表達方式等價,但由於等高線圖比較簡明清晰,所以以後我們都使用等高線圖來說明問題。
程式碼位置
ch03, Level1
系列部落格,原文在筆者所維護的github上:https://aka.ms/beginnerAI,
點選star加星不要吝嗇,星越多筆者越努力。
3.2 交叉熵損失函式
交叉熵(Cross Entropy)是Shannon資訊理論中一個重要概念,主要用於度量兩個概率分佈間的差異性資訊。在資訊理論中,交叉熵是表示兩個概率分佈 \(p,q\) 的差異,其中 \(p\) 表示真實分佈,\(q\) 表示非真實分佈,那麼\(H(p,q)\)就稱為交叉熵:
\[H(p,q)=\sum_i p_i \cdot \ln {1 \over q_i} = - \sum_i p_i \ln q_i \tag{1}\]
交叉熵可在神經網路中作為損失函式,\(p\) 表示真實標記的分佈,\(q\) 則為訓練後的模型的預測標記分佈,交叉熵損失函式可以衡量 \(p\) 與 \(q\) 的相似性。
交叉熵函式常用於邏輯迴歸(logistic regression),也就是分類(classification)。
3.2.1 交叉熵的由來
資訊量
資訊理論中,資訊量的表示方式:
\[I(x_j) = -\ln (p(x_j)) \tag{2}\]
\(x_j\):表示一個事件
\(p(x_j)\):表示\(x_j\)發生的概率
\(I(x_j)\):資訊量,\(x_j\)越不可能發生時,它一旦發生後的資訊量就越大
假設對於學習神經網路原理課程,我們有三種可能的情況發生,如表3-2所示。
表3-2 三種事件的概論和資訊量
| 事件編號 | 事件 | 概率 \(p\) | 資訊量 \(I\) |
|---|---|---|---|
| \(x_1\) | 優秀 | \(p=0.7\) | \(I=-\ln(0.7)=0.36\) |
| \(x_2\) | 及格 | \(p=0.2\) | \(I=-\ln(0.2)=1.61\) |
| \(x_3\) | 不及格 | \(p=0.1\) | \(I=-\ln(0.1)=2.30\) |
WoW,某某同學不及格!好大的資訊量!相比較來說,“優秀”事件的資訊量反而小了很多。
熵
\[H(p) = - \sum_j^n p(x_j) \ln (p(x_j)) \tag{3}\]
則上面的問題的熵是:
\[ \begin{aligned} H(p)&=-[p(x_1) \ln p(x_1) + p(x_2) \ln p(x_2) + p(x_3) \ln p(x_3)] \\ &=0.7 \times 0.36 + 0.2 \times 1.61 + 0.1 \times 2.30 \\ &=0.804 \end{aligned} \]
相對熵(KL散度)
相對熵又稱KL散度,如果我們對於同一個隨機變數 \(x\) 有兩個單獨的概率分佈 \(P(x)\) 和 \(Q(x)\),我們可以使用 KL 散度(Kullback-Leibler (KL) divergence)來衡量這兩個分佈的差異,這個相當於資訊理論範疇的均方差。
KL散度的計算公式:
\[D_{KL}(p||q)=\sum_{j=1}^n p(x_j) \ln{p(x_j) \over q(x_j)} \tag{4}\]
\(n\) 為事件的所有可能性。\(D\) 的值越小,表示 \(q\) 分佈和 \(p\) 分佈越接近。
交叉熵
把上述公式變形:
\[ \begin{aligned} D_{KL}(p||q)&=\sum_{j=1}^n p(x_j) \ln{p(x_j)} - \sum_{j=1}^n p(x_j) \ln q(x_j) \\ &=- H(p(x)) + H(p,q) \end{aligned} \tag{5} \]
等式的前一部分恰巧就是p的熵,等式的後一部分,就是交叉熵:
\[H(p,q) =- \sum_{j=1}^n p(x_j) \ln q(x_j) \tag{6}\]
在機器學習中,我們需要評估label和predicts之間的差距,使用KL散度剛剛好,即\(D_{KL}(y||a)\),由於KL散度中的前一部分\(H(y)\)不變,故在優化過程中,只需要關注交叉熵就可以了。所以一般在機器學習中直接用交叉熵做損失函式來評估模型。
\[loss =- \sum_{j=1}^n y_j \ln a_j \tag{7}\]
其中,\(n\) 並不是樣本個數,而是分類個數。所以,對於批量樣本的交叉熵計算公式是:
\[J =- \sum_{i=1}^m \sum_{j=1}^n y_{ij} \ln a_{ij} \tag{8}\]
\(m\) 是樣本數,\(n\) 是分類數。
有一類特殊問題,就是事件只有兩種情況發生的可能,比如“學會了”和“沒學會”,稱為\(0/1\)分佈或二分類。對於這類問題,由於\(n=2\),所以交叉熵可以簡化為:
\[loss =-[y \ln a + (1-y) \ln (1-a)] \tag{9}\]
二分類對於批量樣本的交叉熵計算公式是:
\[J= - \sum_{i=1}^m [y_i \ln a_i + (1-y_i) \ln (1-a_i)] \tag{10}\]
3.2.2 二分類問題交叉熵
把公式10分解開兩種情況,當\(y=1\)時,即標籤值是1,是個正例,加號後面的項為0:
\[loss = -\ln(a) \tag{11}\]
橫座標是預測輸出,縱座標是損失函式值。y=1意味著當前樣本標籤值是1,當預測輸出越接近1時,損失函式值越小,訓練結果越準確。當預測輸出越接近0時,損失函式值越大,訓練結果越糟糕。
當y=0時,即標籤值是0,是個反例,加號前面的項為0:
\[loss = -\ln (1-a) \tag{12}\]
此時,損失函式值如圖3-10。
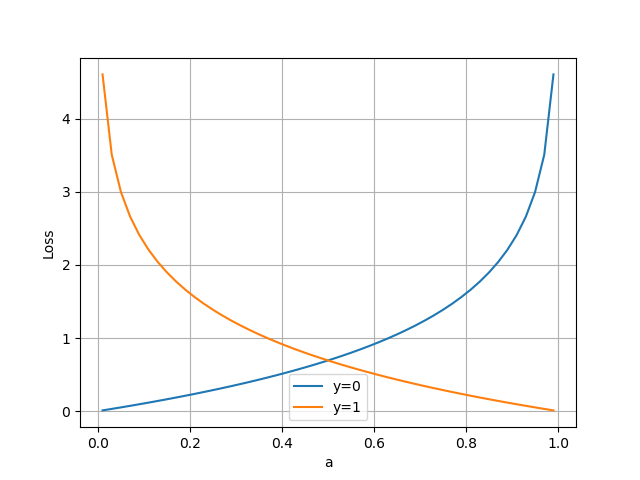
圖3-10 二分類交叉熵損失函式圖
假設學會了課程的標籤值為1,沒有學會的標籤值為0。我們想建立一個預測器,對於一個特定的學員,根據出勤率、課堂表現、作業情況、學習能力等等來預測其學會課程的概率。
對於學員甲,預測其學會的概率為0.6,而實際上該學員通過了考試,真實值為1。所以,學員甲的交叉熵損失函式值是:
\[ loss_1 = -(1 \times \ln 0.6 + (1-1) \times \ln (1-0.6)) = 0.51 \]
對於學員乙,預測其學會的概率為0.7,而實際上該學員也通過了考試。所以,學員乙的交叉熵損失函式值是:
\[ loss_2 = -(1 \times \ln 0.7 + (1-1) \times \ln (1-0.7)) = 0.36 \]
由於0.7比0.6更接近1,是相對準確的值,所以 \(loss2\) 要比 \(loss1\) 小,反向傳播的力度也會小。
3.2.3 多分類問題交叉熵
當標籤值不是非0即1的情況時,就是多分類了。假設期末考試有三種情況:
- 優秀,標籤值OneHot編碼為\([1,0,0]\)
- 及格,標籤值OneHot編碼為\([0,1,0]\)
- 不及格,標籤值OneHot編碼為\([0,0,1]\)
假設我們預測學員丙的成績為優秀、及格、不及格的概率為:\([0.2,0.5,0.3]\),而真實情況是該學員不及格,則得到的交叉熵是:
\[ loss_1 = -(0 \times \ln 0.2 + 0 \times \ln 0.5 + 1 \times \ln 0.3) = 1.2 \]
假設我們預測學員丁的成績為優秀、及格、不及格的概率為:\([0.2,0.2,0.6]\),而真實情況是該學員不及格,則得到的交叉熵是:
\[ loss_2 = -(0 \times \ln 0.2 + 0 \times \ln 0.2 + 1 \times \ln 0.6) = 0.51 \]
可以看到,0.51比1.2的損失值小很多,這說明預測值越接近真實標籤值(0.6 vs 0.3),交叉熵損失函式值越小,反向傳播的力度越小。
3.2.4 為什麼不能使用均方差做為分類問題的損失函式?
迴歸問題通常用均方差損失函式,可以保證損失函式是個凸函式,即可以得到最優解。而分類問題如果用均方差的話,損失函式的表現不是凸函式,就很難得到最優解。而交叉熵函式可以保證區間內單調。
分類問題的最後一層網路,需要分類函式,Sigmoid或者Softmax,如果再接均方差函式的話,其求導結果複雜,運算量比較大。用交叉熵函式的話,可以得到比較簡單的計算結果,一個簡單的減法就可以得到反向誤差。
