鄭重宣告: 本文首發於人工部落格

1、導讀

你能想象到1K的程式碼能寫出什麼樣的功能強大、效果炫酷的作品嗎？來吧，今天小編帶領大家認識下下面這位大神的作品。

西班牙程式設計師Roman Cortes用純JavaScript指令碼編寫的玫瑰花。
這才是牛逼程式設計師送給女友的最好情人節禮物呢！(提示：在不同瀏覽器下觀看效果、速度會有很大的不同)

2、先來張效果圖

線上預覽
預覽效果1:

預覽效果2

3、原理解讀

3.1 蒙特卡羅方法

蒙特卡羅方法是令人難以置信的強大的工具。我用他們所有的時間,對於很多型別的函式優化和抽樣問題,他們幾乎像魔法一樣當你有更多的CPU時間比設計和編碼演算法。在上升的情況下,它是非常有用的程式碼大小的優化。

如果你不知道很多關於蒙特卡羅方法,你可以讀到他們在這個優秀的維基百科文章。

3.2 明確的表面和取樣/繪圖

定義的形狀玫瑰我使用多個explicit-defined表面。我使用一個共有31表面:24花瓣,萼片4(周圍的薄葉花瓣),2葉和1的玫瑰。
這些顯式的表面如此,它們是如何工作的?它是很容易的,我要提供一個二維的例子:
首先我定義明確的表面功能:

function surface(a, b) {  // I'm using a and b as parameters ranging from 0 to 1.
    return {
        x: a*50,
        y: b*50
    };
    // this surface will be a square of 50x50 units of size
}
 

然後,畫它的程式碼:

var canvas = document.body.appendChild(document.createElement("canvas")),
    context = canvas.getContext("2d"),
    a, b, position;

// Now I'm going to sample the surface at .1 intervals for a and b parameters:

for (a = 0; a < 1; a += .1) {
    for (b = 0; b < 1; b += .1) {
        position = surface(a, b);
        context.fillRect(position.x, position.y, 1, 1);
    }
}

 

結果:

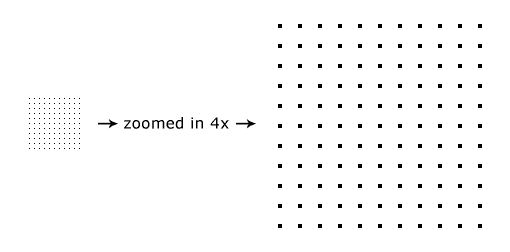
現在,讓我們嘗試更多密集取樣間隔(比間隔=更稠密取樣):

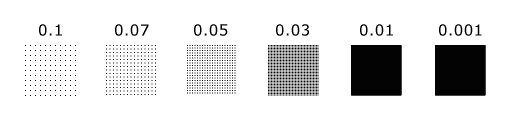
正如你所看到的,當你樣品越來越密集,點越來越近,到密度時的距離從一個點到他們的鄰居比畫素更小,表面是完全填充在螢幕上(見0.01)。之後,讓它更密集的視覺差異,不會引起太大,你只會畫的區域已經(0.01和0.001)的比較結果。
好的,現在讓我們重新定義表面函式畫一個圓。有多種方法,但是我會使用這個公式:(x-x0) ^ 2 + (y-y0) ^ 2 <半徑^ 2,(x0, y0)是圓的中心:

function surface(a, b) {
    var x = a * 100,
        y = b * 100,
        radius = 50,
        x0 = 50,
        y0 = 50;

    if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
        // inside the circle
        return {
            x: x,
            y: y
        };
    } else {
        // outside the circle
        return null;
    }
}




if (position = surface(a, b)) {
    context.fillRect(position.x, position.y, 1, 1);
}

結果:

就像我說的,有不同的方法來定義一個圓,他們中的一些人不需要取樣的拒絕。我將展示一個方法,但是,正如報告;我不會繼續使用它在本文後面:

function surface(a, b) {
    // Circle using polar coordinates
    var angle = a * Math.PI * 2,
        radius = 50,
        x0 = 50,
        y0 = 50;

    return {
        x: Math.cos(angle) * radius * b + x0,
        y: Math.sin(angle) * radius * b + y0
    };
}

(這個方法需要一個密度取樣來填補這個比上一個圈)
好,現在讓變形圓所以它看起來更像一個花瓣:

function surface(a, b) {
    var x = a * 100,
        y = b * 100,
        radius = 50,
        x0 = 50,
        y0 = 50;

    if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
        return {
            x: x,
            y: y * (1 + b) / 2 // deformation
        };
    } else {
        return null;
    }
}

結果:

好,現在這看起來更像玫瑰花瓣的形狀。我建議你玩有點變形。你可以使用任何你想要的數學函式,加、減、乘、除,罪惡,因為,戰俘…任何東西。只是實驗有點修改功能,大量的形狀會出現(一些更有趣,更少)。
現在我想新增一些顏色,所以我要將顏色資料新增到表面:

function surface(a, b) {
    var x = a * 100,
        y = b * 100,
        radius = 50,
        x0 = 50,
        y0 = 50;

    if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
        return {
            x: x,
            y: y * (1 + b) / 2,
            r: 100 + Math.floor((1 - b) * 155), // this will add a gradient
            g: 50,
            b: 50
        };
    } else {
        return null;
    }
}

for (a = 0; a < 1; a += .01) {
    for (b = 0; b < 1; b += .001) {
        if (point = surface(a, b)) {
            context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
            context.fillRect(point.x, point.y, 1, 1);
        }
    }
}

結果:

3.3 3D曲面和透視投影

定義3d曲面很簡單:只需向surface函式新增一個z屬性

function surface(a, b) {
    var angle = a * Math.PI * 2,
        radius = 100,
        length = 400;

    return {
        x: Math.cos(angle) * radius,
        y: Math.sin(angle) * radius,
        z: b * length - length / 2, // by subtracting length/2 I have centered the tube at (0, 0, 0)
        r: 0,
        g: Math.floor(b * 255),
        b: 0
    };
}

現在，新增透視投影，首先我們必須定義一個相機:

結果:

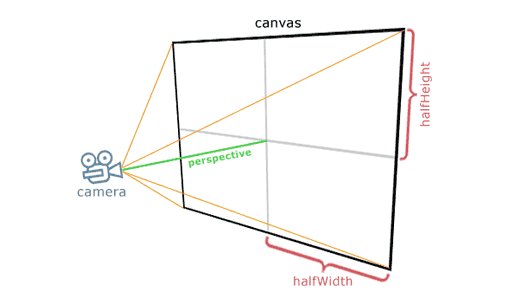
我將我的相機放在(0,0,cameraZ)，我將呼叫“透檢視”的距離，從相機到畫布。我將考慮我的畫布在x/y平面上，以(0,0,cameraZ + perspective)為中心。現在，每個取樣點將被投影到畫布:

var pX, pY,  // projected on canvas x and y coordinates
    perspective = 350,
    halfHeight = canvas.height / 2,
    halfWidth = canvas.width / 2,
    cameraZ = -700;

for (a = 0; a < 1; a += .001) {
    for (b = 0; b < 1; b += .01) {
        if (point = surface(a, b)) {
            pX = (point.x * perspective) / (point.z - cameraZ) + halfWidth;
            pY = (point.y * perspective) / (point.z - cameraZ) + halfHeight;
            context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
            context.fillRect(pX, pY, 1, 1);
        }
    }
}

結果如下：

3.4 Z-buffer

z-buffer是計算機圖形學中很常見的一種技術，它可以在距離攝像機較近的點上繪製距離攝像機較遠的點。它的工作原理是保持一個數組與每畫素畫近z的影象。

這是視覺化的z緩衝的玫瑰，與黑色的相機遠，白色接近它。
實現:

var zBuffer = [],
    zBufferIndex;

for (a = 0; a < 1; a += .001) {
    for (b = 0; b < 1; b += .01) {
        if (point = surface(a, b)) {
            pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth);
            pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight);
            zBufferIndex = pY * canvas.width + pX;
            if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {
                zBuffer[zBufferIndex] = point.z;
                context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
                context.fillRect(pX, pY, 1, 1);
            }
        }
    }
}

3.5旋轉這個圓柱體

你可以使用任何向量旋轉方法。對於玫瑰，我使用了尤拉旋轉。讓我們實現一個繞Y軸的旋轉:

function surface(a, b) {
    var angle = a * Math.PI * 2,
        radius = 100,
        length = 400,
        x = Math.cos(angle) * radius,
        y = Math.sin(angle) * radius,
        z = b * length - length / 2,
        yAxisRotationAngle = -.4, // in radians!
        rotatedX = x * Math.cos(yAxisRotationAngle) + z * Math.sin(yAxisRotationAngle),
        rotatedZ = x * -Math.sin(yAxisRotationAngle) + z * Math.cos(yAxisRotationAngle);

    return {
        x: rotatedX,
        y: y,
        z: rotatedZ,
        r: 0,
        g: Math.floor(b * 255),
        b: 0
    };
}

3.6 蒙特卡洛取樣

我在文章中使用了基於時間間隔的抽樣。它需要為每個表面設定一個適當的間隔。如果間隔很大，渲染速度會很快，但最終會在表面留下一些沒有填充的洞。另一方面，如果間隔太短，則呈現增量的時間會達到無法接受的數量。
那麼，讓我們切換到蒙特卡羅抽樣:

var i;

window.setInterval(function () {
    for (i = 0; i < 10000; i++) {
        if (point = surface(Math.random(), Math.random())) {
            pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth);
            pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight);
            zBufferIndex = pY * canvas.width + pX;
            if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {
                zBuffer[zBufferIndex] = point.z;
                context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
                context.fillRect(pX, pY, 1, 1);
            }
        }
    }
}, 0);

現在，a和b引數被設定為兩個隨機值。取樣足夠的點，表面就會以這種方式完全填充。我每次畫10000個點然後讓螢幕根據間隔更新。

另外，只有在偽隨機數發生器質量良好的情況下，才能保證曲面的完全填充。在一些瀏覽器中，數學。隨機是用一個線性同餘發生器實現的，這可能會導致一些曲面的問題。如果你需要一個好的PRNG取樣，你可以使用高質量的像Mersenne Twister(它有JS實現)，或者在一些瀏覽器中可用的加密隨機生成器。使用低差異序列也是非常明智的。

4、總結

完成玫瑰，玫瑰的每一部分，每一個表面，都是同時呈現的。我為函式添加了第三個引數，該函式選擇玫瑰的部分來返回一個點。數學上它是一個分段函式，每一塊都代表玫瑰的一部分。在花瓣的例子中，我使用旋轉和拉伸/變形來建立所有的花瓣。所有的工作都是通過混合本文中暴露的概念來完成的。

雖然通過取樣顯式表面是一種非常著名的方法，也是最古老的3d圖形方法之一，但我的分段/蒙特卡羅/z-buffer方法可能很少像我這樣用於藝術目的。雖然不是非常具有創新性，在實際場景中也不是很有用，但是它非常適合js1k的環境，在這種環境中，簡單性和最小的大小都是需要的。

通過這篇文章，我真的希望能夠激勵那些對計算機圖形感興趣的讀者去嘗試和享受不同的渲染方法。在圖形領域有一個完整的世界，研究和使用它是令人驚奇的。

版權宣告：本文為人工部落格的原創文章，遵循 CC 4.0 BY-SA 版權協議，轉載請附上原文出處連結及本宣告。
本文連結：https://www.94rg.com/article/1724