重學資料結構 --- 分類+稀疏陣列
阿新 • • 發佈:2020-01-22
一、資料結構的分類
1. 資料結構兩大類
線性結構和非線性結構
1) 線性結構
- 線性結構是最常見的資料結構,特點是元素間存在一對一的線性關係。
- 線性結構又分兩種,一種是順序儲存(稱為順序表),另外一種是鏈式儲存(稱為連結串列)。順序表中的儲存元素的連續的。連結串列中的儲存元素不一定是連續的,元素節點中存放資料元素以及相鄰元素的地址資訊。
- 常見的線性結構有:陣列、佇列、連結串列和棧(這裡只是講個大概,具體內容後面的文章會展開闡述)。
2) 非線性結構
非線性結構就是結點元素可能存在多個直接前趨和多個直接後續(聯想一下二叉樹就懂了,但是非線性結構不僅僅只有二叉樹)。
- 非線性結構包括:多維陣列、廣義表、樹結構、圖結構。
二、稀疏陣列
1. 稀疏陣列(sparse array)
1) 分析場景
有這麼一個場景,需要實現一個 10*10 的圍棋的步數記錄。那麼最簡單的就可以使用一個二維陣列int[10][10]便可,但是在棋盤伊始,這個二維陣列幾乎沒有意義的資料。假如能找到將這個二維陣列壓縮,只記錄有用的資料的方法就好了。這時候稀疏陣列就可以派上用場了。
2) 稀疏陣列
像上述棋盤,開始的時候,資料中記錄的大部分元素為 0,或者為同一個值的陣列時,可以使用稀疏陣列來儲存該陣列。
3) 稀疏陣列的處理方法是:
- 記錄陣列一共有幾行幾列,有多少個不同的值
把具有不同的元素的行列以及值記錄在一個小規模的陣列中,從而壓縮小程式的規模。
4) 舉個例子:
假如有如下的 10*6的棋盤,用正整數表示落子順序,使用稀疏陣列壓縮該棋盤則有右側的表示。第 0 行,分別表示:行數,列數,總有多少個值。從第 1 行開始到最後,都表示行數,列數,數值。
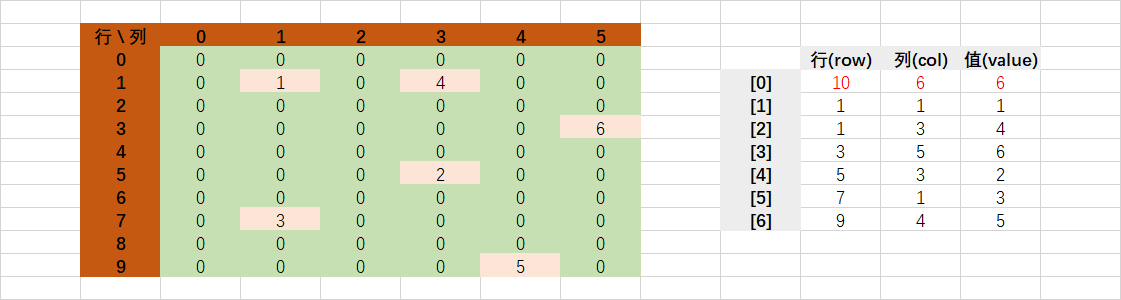
如此一來,本來是 610 的陣列就被壓縮成 37,大大節省了記憶體空間。
5) 程式碼實現
思路分析
(1) 二維陣列轉稀疏陣列
- 遍歷原始二維陣列,得到有效資料的個數 sum
- 建立稀疏陣列 sparseArr[sum+1][3]
- 把有效資料逐個填入稀疏陣列 sparseArr 中
- 程式碼實現:
/** * 二維陣列轉稀疏陣列 * * @param arr 原陣列 * @return 稀疏陣列 */ public int[][] reserveSparseArray(int[][] arr) { // 統計有效資料 int sum = 0; // 遍歷稀疏陣列 for (int[] is : arr) { for (int num : is) { if (num != 0) { sum++; } } } // 建立稀疏陣列 int[][] sparseArr = new int[sum + 1][3]; sparseArr[0][0] = arr.length; sparseArr[0][1] = arr[0].length; sparseArr[0][2] = sum; for (int i = 0; i < arr.length; i++) { for (int j = 0; j < arr[i].length; j++) { if (arr[i][j] != 0) { sparseArr[sum][0] = i; sparseArr[sum][1] = j; sparseArr[sum][2] = arr[i][j]; sum--; } } } return sparseArr; }
(2) 稀疏陣列轉原始陣列
- 讀取稀疏陣列的第 1 行,取出第一 row、第二個數 col,建立二維陣列 shessArr[row][col]
- 遍歷稀疏陣列後面幾行,把有效值填入原陣列 chessArr
- 程式碼實現:
/**
* 稀疏陣列轉二位陣列
*
* @param sparseArr 稀疏陣列
* @return 原陣列
*/
public static int[][] reserveOriginalArray(int[][] sparseArr) {
// 根據稀疏陣列第一行建立原陣列
int[][] originalArr = new int[sparseArr[0][0]][sparseArr[0][1]];
// 把稀疏陣列的值放回到原陣列中
for (int i = 1; i < sparseArr.length; i++) {
int row = sparseArr[i][0];
int col = sparseArr[i][1];
int value = sparseArr[i][2];
originalArr[row][col] = value;
}
return originalArr;
}人若無名,專心練劍!
喜歡的朋友可以留下你的贊!
