【資料結構】FHQ Treap詳解
FHQ Treap是什麼?
FHQ Treap,又名無旋Treap,是一種不需要旋轉的平衡樹,是範浩強基於Treap發明的。FHQ Treap具有程式碼短,易理解,速度快的優點。(當然跟紅黑樹比一下就是……)至少它在OI中算是很優秀的資料結構了。
前置知識:
C++二叉搜尋樹的基本性質,下面會講二叉堆
二叉搜尋樹的基本性質
很簡單,就這幾個。
- 在
二叉搜尋樹中,每個結點都滿足左子樹的結點的值都小於等於自己的值,右子樹的結點的值都大於自己的值,左右子樹也是二叉搜尋樹。 - 中序遍歷
二叉搜尋樹可以得到一個由這棵樹的所有結點的值組成的有序序列。(即所有的值排序後的結果)
原理&程式碼實現
本文中,
Treap就是指有旋Treap
FHQ Treap不是通過旋轉來保持平衡的,而是通過兩個函式split和merge。顧名思義,split就是分裂,merge就是合併。當然,從最底層的原理來看,還不是這兩個函式。FHQ Treap中的Treap代表Tree + Heap,也就是說,FHQ Treap會按二叉搜尋樹一樣根據鍵值排序結點,並且隨機賦給每個結點一個優先順序,按照二叉堆的順序排序結點(這裡用大根堆)。Treap通過旋轉,使平衡樹同時滿足這兩個性質,從而達到平衡。而FHQ Treap通過呼叫merge函式時使平衡樹滿足堆序,實現原理與Treap不同。
結點資訊
FHQ Treap
template <typename T, int MaxSize> class FHQTreap { public: FHQTreap() { Seed = (int)(MaxSize * 565463ll % 2147483647); } // ... private: struct Node { T Key; int Left, Right, Size, Priority; } Tree[MaxSize]; int Seed, Total, Root; int random() { return Seed = (int)(Seed * 104831ll % 0x7fffffff); } void pushup(int root) { if(root != 0) { Tree[root].Size = Tree[Tree[root].Left].Size + Tree[Tree[root].Right].Size + 1; // + 1是要算上自己 } } // ... }
Node即結點,裡面的Key就是要存的值,Priority即優先順序。Seed就是隨機數種子,在建構函式中初始化,random()會生成一個在int範圍內的整數,作為結點的優先順序。(我自己寫隨機數生成函式只是個人習慣)
構造新結點
int create(T key) {
int root = ++Total;
Tree[root].Key = key;
Tree[root].Size = 1;
Tree[root].Left = Tree[root].Right = 0;
Tree[root].Priority = rad();
return root;
}create(T key)會初始化一個結點,並返回它的ID,大家也可以用指標實現。這裡比較簡單,就不多解釋了。
split函式
split分為兩種:
- 按值分裂:根據一個值\(key\)把一棵樹分裂成兩棵樹,一棵樹的值全部小於等於\(key\),另外一棵全部大於\(key\)
- 按大小分裂:根據一個值\(size\)分裂樹,一棵的大小為\(size\),另外一棵為剩下的。
按值分裂
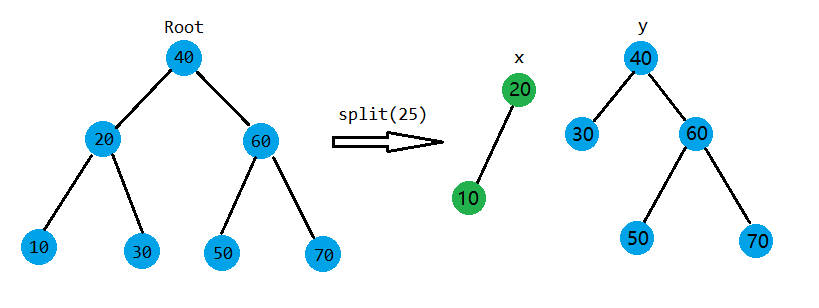
如上圖。這裡split函式簡化了,只寫了值。根據圖可以看出,比\(25\)小的結點都被分裂到以\(x\)為根的樹上,比\(25\)大的結點被分到了\(y\)樹上。
那我們該怎麼寫呢?如果我們到了一個結點\(root\),假設\(X,Y\)是分裂後的兩棵樹,且滿足\(\forall i \in X,j \in Y ,\exists Key_{i} < Key_{j}\),要是\(Key_{root} \leq key\),那它就應該被放到\(X\)樹上,否則它應該被放到\(Y\)樹上。如果它被放到了\(X\)樹上,我們還要再檢查一下是否有結點\(z\),滿足\(Key_{root} \leq Key_{z} \leq key\),如果有,也要插入\(X\)樹,具體的操作就是把\(z\)掛到\(root\)的右子樹上,這可以通過繼續遞迴呼叫split函式實現。如果滿足\(Tree[root].Key > key\),就做一次相反的過程。
void split(int root, int key, int &x, int &y) { // x, y即分裂出的兩個樹
if (root == 0) {
x = y = 0;
return;
}
if (!(key < Tree[root].Key)) { // 等價於 Tree[root].Key <= key
x = root; // 把root設為x樹的根(當前)
split(Tree[root].Right, key, Tree[root].Right, y); // 找更大的結點
} else {
y = root; // 相反過程
split(Tree[root].Left, key, x, Tree[root].Left);
}
pushup(root); // 記得更新大小
}按大小分裂
與按值分裂類似,把值換成大小,注意遞迴右子樹時要把\(size\)減去\(Size_{Left_{x}}+1\),這也是顯然的。
void split(int root, int sze, int &x, int &y) {
if(root == 0) {
x = y = 0;
return;
}
if (Tree[Tree[root].Left].Size + 1 <= sze) {
x = root;
split(Tree[root].Right, sze - Tree[Tree[root].Left].sze - 1, Tree[root].Right, y);
} else {
y = root;
split(Tree[root].Left, sze, x, Tree[root].Left);
}
pushup(root);
}merge函式
我比較懶,把上面那個圖複製貼上了一下。
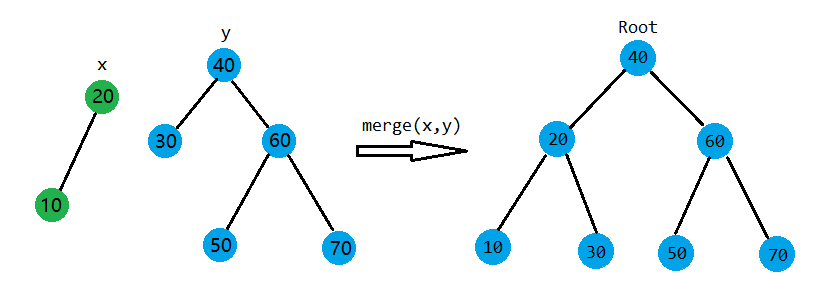
假設\(X,Y\)是需要合併的兩棵樹,且滿足\(\forall i \in X,j \in Y ,\exists Key_{i} < Key_{j}\),\(x\)為\(X\)根節點,\(y\)為\(Y\)根節點。所以,在合併的時候,我們只要按照優先順序,看一下是把\(x\)放在上還是把\(y\)放在上。以下是\(x,y\)在不同的優先順序關係下的樹的結構:
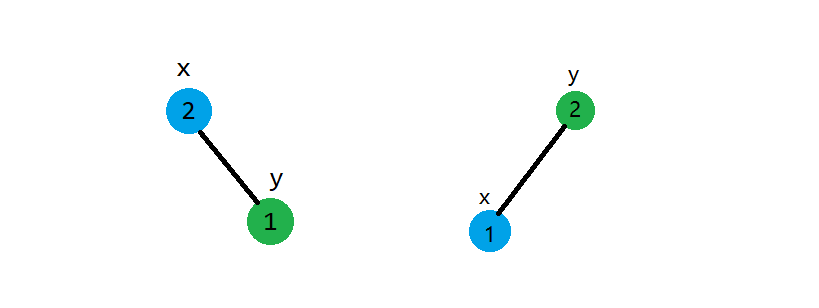
如果我們已經確定好了\(x,y\)這兩個點的結構,那就直接拿那個被替換的子樹與在下面的結點去merge。說起來比較抽象,我們就用上面那個圖的左邊那種情況作為例子(這個圖是隻考慮\(x,y\)兩個結點的,並沒有算上它們的子樹)。\(x\)的優先順序比\(y\)的優先順序大(按照大根堆),那麼\(x\)就在上,\(y\)在下。那麼有要滿足二叉搜尋樹的性質,\(y\)的值比\(x\)大,則\(y\)在右邊,即在\(x\)的右子樹。如果在考慮\(x,y\)兩個結點都子樹的情況,\(x\)的左子樹不動,把\(y\)和\(x\)的右子樹合併的結果作為\(x\)新的右子樹。另外一種情況同理。
int merge(int x, int y) {
if (x == 0 || y == 0)
return x + y;
/*
如果其中一個結點為空,即只剩另下一棵樹需要處理,就直接返回
因為空結點的ID為0,所以直接返回 x + y 即可。 如果兩棵樹都為空,這樣也是沒有問題的。
*/
if (Tree[x].Priority > Tree[y].Priority) {
Tree[x].Right = merge(Tree[x].Right, y);
pushup(x);
return x;
} else {
Tree[y].Left = merge(x, Tree[y].Left);
pushup(y);
return y;
}
}各種修改&查詢
插入
假設插入的值為\(key\),把樹分裂按\(key-1\)分裂成兩棵,在中間新建結點,合併。
void insert(T key) {
int x, y;
split(Root, key - 1, x, y);
Root = merge(merge(x, create(key)), y);
}刪除
假設刪除的值為\(key\),把樹分裂按\(key\)分裂成\(X,Z\),把\(X\)按\(key-1\)分裂成\(X,Y\)。這裡\(Y\)上的結點的值都等於\(key\)。如果只刪除一個結點,就把\(Y\)賦值為它的左右子樹合併的結果,在合併\(X,Y,Z\)。如果刪除所有,就直接合並\(X,Z\)。
void remove(T key) {
int x, y, z;
split(Root, key, x, z);
split(x, key - 1, x, y);
if(y) { // 如果刪除所有,就直接去掉這個if語句塊,並且下面的只合並x, z
y = merge(Tree[y].Left, Tree[y].Right);
}
Root = merge(merge(x, y), z);
}查詢指定值的排名
如果是在一個有序的序列中查詢排名,我們可以二分查詢這個序列,然後根據找到的元素的下標來確定排名,假設下標從\(1\)開始,那麼排名就為該元素的下標\(i\)。那麼,在它之前,也就有\(i-1\)個元素。由此,我們可以得到排名的一種定義:在有序序列中,一個元素的排名就是它前面的元素的個數\(+1\)。
在FHQ Treap上,我們就直接按\(key-1\)分裂樹,查一下值小於等於\(key-1\)的樹的大小,再\(+1\)即可。
int rank(T key) {
int x, y, ans;
split(Root, key - 1, x, y);
ans = Tree[x].Size + 1;
Root = merge(x, y);
return ans;
}查詢指定排名的值
寫法1
從根節點開始,根據左子樹的\(size+1\)確定往哪裡走,分三種情況。
- \(size+1=rank\),找到答案
- \(size+1>rank\),在左子樹
- \(size+1<rank\),在右子樹
T at(int r) {
int root = Root;
while (true) {
if (Tree[Tree[root].Left].Size + 1 == r) {
break;
} else if (Tree[Tree[root].Left].Size + 1 > r) {
root = Tree[root].Left;
} else {
r -= Tree[Tree[root].Left].Size + 1;
root = Tree[root].Right;
}
}
return Tree[root].Key;
}寫法2
根據按大小分裂,把樹分裂成三棵,取中間那棵的值。
// 這裡的split是按大小分裂
T at(int r) {
int x, y, z;
split(Root, r - 1, x, y);
split(y, 1, y, z);
T ans = Tree[y].Key;
Root = merge(merge(x, y), z);
return ans;
}推薦大家用寫法1,總的程式碼更少,速度更快。
查詢前驅
前驅,即最大的小於被查詢元素的元素
按\(key-1\)分裂樹,在值小於等於\(key-1\)的樹上一直向右下走,就是走到中序遍歷的最後一個結點,合併後返回值即可。
T lower(T key) {
int x, y, root;
T ans;
split(Root, key - 1, x, y);
root = x;
while (Tree[root].Right) root = Tree[root].Right;
ans = Tree[root].Key;
Root = merge(x, y);
return ans;
}查詢後繼
後繼,即最小的大於被查詢元素的元素
和查詢前驅一樣的。就是在另外一棵樹上往左下走。
T upper(T key) {
int x, y, root;
T ans;
split(Root, key, x, y);
root = y;
while (Tree[root].Left) root = Tree[root].Left;
ans = Tree[root].Key;
Root = merge(x, y);
return ans;
}查詢樹的大小
直接返回根節點記錄的大小。
int size() {
return Tree[Root].Size;
}查詢一個元素是否存在
把樹分裂為三棵,中間那棵的值全部等於\(key\),再看看中間的樹的大小是否不為\(0\),不為\(0\)則有這個元素。
bool find(T key) {
int x, y, z;
split(Root, key, x, z);
split(x, key - 1, x, y);
bool ans;
if(Tree[y].Size) ans = true;
else ans = false;
Root = merge(merge(x, y), z);
return ans;
}垃圾回收優化
對於那些被刪除的結點,我們可以把它們存起來,新建結點時使用。
需要修改的函式:
// Stack[]即棧,用來儲存結點,也可以使用std::stack<T>
void remove(T key) {
int x, y, z;
split(Root, key, x, z);
split(x, key - 1, x, y);
if(y) {
if(Top < (MaxSize << 8) - 5) Stack[++Top] = y;
y = merge(Tree[y].Left, Tree[y].Right);
}
Root = merge(merge(x, y), z);
}
int create(T key) {
int root = Top ? Stack[Top--] : ++Total;
Tree[root].Key = key;
Tree[root].Size = 1;
Tree[root].Left = Tree[root].Right = 0;
Tree[root].Priority = rad();
return root;
}完整實現
不貼程式碼了,來GitHub,網速慢請稍等或準備梯子(當然不會慢到那種地步)。
例題
普通平衡樹
- 題目:LOJ 104
- 程式
平衡樹板子題,直接複製GitHub的程式碼再加上標頭檔案和main函式就可以\(AC\)了。(知道你們最喜歡\(AC\)了)
文藝平衡樹
- 題目:LOJ 105
- 程式
時間原因,碼風有點不一樣,就湊合這看吧。
我們可以給每個結點多維護一個資訊——翻轉標記。對於翻轉的每個區間\([l,r]\),我們可以按大小分裂,實現按\(l-1\)分裂出\(X,Y\),再將\(Y\)按\(r-l+1\)分裂為\(Y,Z\)。給\(Y\)樹大上翻轉標記即可。再考慮標記下傳,如果一個結點沒有被翻轉(被翻轉偶數次也算沒有翻轉),就直接返回,否則去除當前結點的翻轉標記,給子結點的翻轉標記取反(或異或\(1\)),交換兩個子結點。同時,在split函式和merge函式裡新增標記下傳程式碼。
實現細節如下:
void pushdown(int rt) {
if (tree[rt].rev == 0)
return;
swap(tree[rt].l, tree[rt].r);
tree[tree[rt].l].rev ^= 1;
tree[tree[rt].r].rev ^= 1;
tree[rt].rev = 0;
}
void split(int rt, int sze, int &x, int &y) {
if (rt == 0) {
x = y = 0;
return;
}
pushdown(rt);
if (tree[tree[rt].l].sze + 1 <= sze) {
x = rt;
split(tree[rt].r, sze - tree[tree[rt].l].sze - 1, tree[rt].r, y);
} else {
y = rt;
split(tree[rt].l, sze, x, tree[rt].l);
}
pushup(rt);
}
int merge(int x, int y) {
if (x == 0 || y == 0)
return x + y;
if (tree[x].pri > tree[y].pri) {
pushdown(x);
tree[x].r = merge(tree[x].r, y);
pushup(x);
return x;
} else {
pushdown(y);
tree[y].l = merge(x, tree[y].l);
pushup(y);
return y;
}
}
void reverse(int l, int r) {
int x, y, z;
split(root, l - 1, x, y);
split(y, r - l + 1, y, z);
tree[y].rev ^= 1;
root = merge(merge(x, y), z);
}最後按題目要求輸出即可。
鬱悶的出納員
- 題目:LOJ 10145
- 程式
本來這到題用Treap是需要打標記的,但是有了FHQ Treap就是個簡單題了。如果給員工減工資,就先遍歷一遍,然後對樹split,把小於\(min\)的那棵樹直接扔掉,並把它的大小加入答案。其他都沒有什麼問題了。
如果你也是自己寫隨機函式,一定要記得初始化種子,否則你會像我之前一樣
random()總是返回\(0\),最後卡成了鏈,T飛了。
