Latent Representation Learning For Artificial Bandwidth Extension Using A Conditional Variational Auto-Encoder
部落格作者:凌逆戰
論文地址:https://ieeexplore.ieee.xilesou.top/abstract/document/8683611/
地址:https://www.cnblogs.com/LXP-Never/p/10714401.html
利用條件變分自動編碼器進行人工頻寬擴充套件的潛在表示學習
作者:Pramod Bachhav, Massimiliano Todisco and Nicholas Evans
摘要
當寬頻裝置與窄帶裝置或基礎設施一起使用時,人工頻寬擴充套件(ABE)演算法可以提高語音質量。大多數ABE解決方案都使用某種形式的memory(記憶),這意味著高維特性表示會增加延遲和複雜性。因此發展了降維技術以保持效率。因此提取緊湊的低維表示,然後與標準迴歸模型一起用於估計高頻段分量。
以往的研究表明,某種形式的監督對於優化ABE的降維技術至關重要。本論文研究了條件變分自動編碼器(conditional variational auto-encoders,CVAEs)在監督降維中的首次應用。利用有向圖模型的CVAEs對高維對數譜資料進行建模,提取潛在的窄帶表示法。
與其他降維技術的結果相比,客觀和主觀的評估表明,使用CVAEs學習的潛在概率表示產生的頻寬擴充套件語音訊號質量顯著提高。
index Terms(索引項):變分自動編碼器,潛在變數,人工頻寬擴充套件,降維,語音質量
1 介紹
傳統窄帶(NB)網路和裝置通常支援0.3-3.4kHz的頻寬。為了提高語音質量,今天的寬頻(WB)網路支援50Hz-7kHz的頻寬。隨著NB網路向WB網路的過渡,需要大量的投資[1],人工頻寬擴充套件(ABE)演算法被開發出來,當WB裝置與NB裝置或基礎設施一起使用時,可以提高語音質量。ABE用於從可用NB分量中估計缺失的3.4kHz以上的highband(高帶)(HB)頻率分量,通常使用從大量WB訓練資料中學習的迴歸模型。
ABE演算法要麼使用經典的源濾波器模型[2,3],要麼直接對複雜的短期頻譜估計進行操作[4,6]。在這兩種方法中,使用contextual information(上下文資訊)或memory(記憶),可以更可靠地估計HB成分。一些特定的back-end(後端)regression(迴歸)模型[7 9]以時間資訊的形式捕獲memory,而其他解決方案[4、10、11]則相反地在front-end(前端)捕獲記憶,例如通過delta特徵或從相鄰幀提取的靜態特徵。雖然memory的使用提高了ABE的效能,但它意味著使用更高維度的特性,因此,ABE迴歸模型更復雜,計算要求更高。考慮到ABE通常需要在電池驅動的裝置上執行,這是不可取的。
為了減少複雜性的增加,[12,13]研究了在固定維度的約束下,通過delta mel頻率倒譜系數(MFCC)包含記憶。然而,研究發現,互資訊的增益被MFCC inversion(轉換)中涉及的重建偽影所抵消[13]。我們自己的工作[14]提出了一種方法,將memory(記憶)以相鄰幀的靜態特性的形式包含進來。為了保持效率,採用了降維方法。我們後續的工作[15]表明,由對數譜系陣列成的memory(記憶)可以使用半監督堆疊自動編碼器(semi-supervised stacked auto-encoders, SSAE)學習一種緊湊的、低維的ABE特徵表示。本文的工作旨在探索生成建模技術的應用,以進一步提高ABE效能。目標是對高維譜資料(包括memory(記憶))的分佈建模,並提取更高層次、更低維的特徵,從而在不影響複雜性的情況下提高ABE迴歸模型的可靠性。從本質上講,我們尋求一種專門針對ABE的降維(DR)形式。
變分自編碼器(VAEs)及其條件變分自動編碼器(CVAEs)概率深度生成模型能夠對複雜的資料分佈進行建模。與堆疊式自動編碼器(SAEs)學習的瓶頸特性相比,隱藏表示是概率的,可以用來生成新的資料。受其在影象處理中的成功應用[16 18]的啟發,它們在眾多的語音處理領域越來越受歡迎,如語音建模與轉換[19,20]、語音轉換[21]、語音合成[22]、語音增強用於語音活動檢測[23]、情感識別[24]和音訊源分離[25]。
CVAEs通過combination(聯合)潛在變數和條件變數來生成資料。本文工作的思路是通過輔助神經網路對條件變數進行優化,以學習higher-level(更高層次)的NB特徵,這些特徵是針對ABE任務中缺失HB分量的估計而定製的。這項工作的新貢獻是:
(i) 第一次將VAEs和CVAEs應用於DR的迴歸任務,如ABE;
(ii) 將CVAE與probabilistic encoder(概率編碼器)結合,以auriliary(輔助)神經網路的形式,得到條件變數;
(iii) 聯合優化的一種方法;
(iv) 他們應用於extract(提取)probabilistic(概率)NB潛在表示,以估計在其他標準ABE框架中丟失的HB資料;
(v) 所提出的方法來大幅提高ABE效能。
本文的其餘部分組織如下。第2節描述了基線ABE演算法。第3節介紹了基於VAE和CVAE的特徵提取方案,第4節實驗,第5節結論。
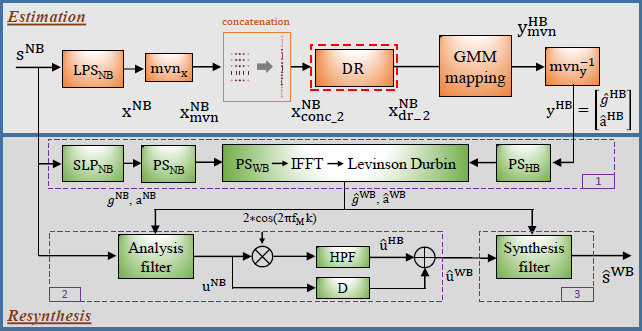
圖1 基線ABE系統框圖。圖改編自[14]
2 基線系統
圖1顯示了基線ABE系統。它與[14](作者自己的文章)中提出的基於源濾波器模型的方法是一致的。因此,這裡只提供一個簡要的概述。該演算法由 估計 和 再合成 兩部分組成。
Estimation(估計) 使用1024點FFT處理持續時間為20 ms、取樣率為16kHz的NB語音幀sNB,extract(提取)200維NB對數功率譜(LPSNB)係數xNB,該係數經過均值和方差歸一化(mvn_x)得到的$x_{mvn}^{NB}$。在appent(相加)了2個相鄰幀的係數後,得到1000維concatenate(級聯)向量$x_{conc\_2}^{NB}$。應用降維(DR)技術提取10維的特徵向量$x_{dr\_2}^{NB}$。然後使用傳統的基於GMM的對映技術進行估計[2]得到歸一化的HB特徵$y_{mvn}^{HB}$由9個LP係數和一個gain(增益)引數組成。然後應用反向均值方差歸一化($mvn_y^{-1}$)得到HB特徵$y^{HB}$。
Resynthesis(再合成)
- 首先(框1),通過選擇性線性預測(SLPNB)從語音幀sNB中得到LP引數aNB、gNB,用來得到NB功率譜PSNB。然後將其與HB功率譜PSHB(從HB LP引數$\hat{g}^{HB}$,$\hat{a}^{HB}$中estimated(估計)得到) concatenated(級聯),得到WB功率譜PSWB,從而估計WB LP引數$\hat{g}^{HB}$,$\hat{a}^{HB}$。
- 其次(框2),HB激勵$\hat{u}^{HB}$是根據NB激勵uNB在6.8kHz時的頻譜translation(轉換)然後經過高通濾波來估算的。然後將NB和HB激勵分量相結合,得到擴充套件的WB激勵$\hat{u}^{WB}$。
- 最後(框3),使用$\hat{g}^{WB}$和$\hat{a}^{WB}$定義的合成濾波器對$\hat{u}^{WB}$進行濾波,以重新合成語音幀$\hat{s}^{WB}$。採用傳統的overlap(重疊)和相加(overlap and add,OLA)技術來產生擴充套件的WB語音。
3 使用條件變分自動編碼器進行特徵提取
在本節中,我們展示瞭如何將VAE和CVAE體系結構的聯合學習用於特徵提取,以提高ABE效能。
3.1 VAE(變分自動編碼器)
變分自動編碼器(variational,VAE)[26]是一個生成模型$p_\theta (x,z)=p_\theta (z)p_\theta (x|z)$(帶引數$\theta$),假設其中的資料$\{x^{(i)}\}_{i=1}^N$由N個i組成。隨機變數$x$的樣本由連續的潛在變數$z$生成,在實際中,求解marginal likelihood(邊界似然)$p_{\theta}(x)$和true posterior density(真實後驗密度)$p_{\theta}(z|x)$都是棘手的,為了解決這個問題,VAEs使用一個recognition/inference(識別/推理)模型$q_\phi (z|x)$作為後驗$p_{\theta}(z|x)$的近似值,單個數據點的邊界似然為:
$$公式1:\log p(x)=-D_{KL}[q_\phi (z|x)||p_\theta(z|x)]+L(\theta,\phi ;x)$$
其中第一項表示近似後驗分佈和真實後驗分佈之間的Kullback-Leibler (KL)散度(DKL)。為了簡單起見,假設近似後驗和真後驗為對角多元高斯分佈,用兩種不同的深度神經網路計算其各自的引數$\theta$和$\phi$。
由於KL散度為非負的,$L(\theta,\phi ;x)$表示marginal likelihood(邊界似然)的variational(變分)下界,可寫為:
$$公式2:L(\theta,\phi ;x)=-D_{KL}[q_{\phi} (z|x)||p(z)]+E_{z_\phi }[\log p_\theta(x|z)]$$
其中,$D_{KL}[·]$作為正則化項,可以通過分析計算得出。在實際應用中,假定先驗$p(z)=N(z;0,I)$是中心各向同性多元高斯,沒有自由引數。第二項是預期的負重建誤差,必須通過抽樣估計。使用從識別網路$q_\phi (z|x)$中samples(抽取)的$L$個樣本,將其近似為$\frac{1}{L}\sum_{l=1}^L\log p_\theta(x|z^{(l)})$。使用可微確定性對映進行取樣,這樣$z^{{l}}=g_\phi (x,\epsilon ^{(l)})=\mu (x)+\epsilon ^{(l)}\odot \sigma (x)$,其中$\epsilon ^{(l)}\sim N(0,I)$。$\mu _z=\mu (x)$和$\sigma _z=\sigma(x)$是識別網路$q_\phi (z|x)$的輸出。這被稱為reparameterization trick(重新引數化技巧)。下界$L$構成目標函式,利用隨機梯度下降演算法對引數$\theta$和$\phi $進行優化。
3.2 CVAE(條件變分自動編碼器)
條件變分自動編碼器(CVAE)是一個條件生成模型$p_\theta(y,z|x)=p_\theta(z)p_\theta(y|x,z)$;對於給定的輸入$x$,從先驗分佈$p_\theta(x)$中提取潛在變數$z$,其中分佈$p_\theta(y|x,z)$生成輸出$y$[17,18]。為了處理棘手的問題,CVAEs也使用近似後驗$q_\phi (z|x,y)$。
我們採用了與[18]不同的公式,其中我們假設潛在變數只依賴於輸出變數$y$,即$q_\phi (z|x,y)=q_\phi(z|y)$。條件似然$p_\theta(y|x)$的變分下界由下式給出:
$$公式3:\log p_\theta(y|x)\geq L(\theta ,\phi ;x,y)=-D_{KL}[q_\phi (z|y)||p_\theta(z)]+E_{q_\phi (z|y)}[\log p_\theta(y|x,z)]$$
第二項近似為$\frac{1}{L}\sum_{l=1}^L\log p_\theta(y|x,z^{(l)})$;其中$z^{(l)}=g_\phi (y,\epsilon ^{(l)})=\mu (y)+\epsilon ^{(l)}\odot \sigma (y)$其中$\epsilon ^{(l)}\sim N(0,I)$和$\sigma _z=\sigma (y)$是識別網路$q_\phi (y|x,z)$的輸出。實際上,每個datapoint(資料點)[26]使用L = 1個樣本。CVAE識別網路$q_\phi (z|y)$和生成網路$p_\theta(y|x,z)$採用深度神經網路建模。
公式3中的輸出分佈$p_\theta(y|x,z)$取高斯函式,平均值為$f(x,z;\theta)$並且covariance matrix(協方差矩陣)為$\sigma^2*I$,即$p_\theta(y|x,z)=N(f(x,z;\theta),\sigma ^2*I)$其中$f$是帶有引數$\theta$的x和z的確定性變換。因此
$$公式3:\log p_\theta(y|x,z)=C-||y-f(x,z;\theta)||^2/\alpha $$
其中C是一個常數,在優化過程中可以忽略。標量$\alpha =2\sigma ^2$可以看作是KL-divergence(KL散度)與重構項[27]之間的權重因子。
3.3 提取ABE的潛在表示
本節描述了聯合優化VAE和CVAE的方案,為了學習到針對ABE的潛在表示。方案如圖2所示。並行訓練資料由NB和WB語句組成,幀長為20ms,重疊為10ms。輸入資料$x=x_{conc\_2}^{NB}$由帶memory(記憶)的NB LPS係數組成(如第2節所述),輸出資料$y=y_{mvn}^{HB}$由9個LP係數和一個從並行HB資料中通過選擇性線性預測(SLP)提取的增益引數組成。
首先對VAE進行訓練,將編碼器$q_{\phi_x}(z_x|x)$(圖2底部)由輸入資料x進行fed(饋送),以預測均值$\mu_{z_x}$和代表後驗分佈$q_{\phi_x}(z_x|x)$的log-variance(對數方差)$\log (\sigma _{z_x}^2)$。將對應的解碼器$p_{\theta_x}(x|z_x)$(圖2未表示出)由輸入$z_x\sim q_{\phi _x}(z_x|x)$進行饋送,以預測分佈$p_{\theta_x}(x|z_x)$的均值$\mu _x$。這可以看作是初始化編碼器$q_{\phi_x}(z_x|x)$權值的某種形式的預訓練。注意,在這個階段,NB表示$z_x$是在沒有任何HB資料監督的情況下學習的。然後丟棄VAE解碼器。然後使用編碼器$q_{\phi_x}(z_x|x)$作為CVAE的條件變數(如圖2所示)。
然後訓練CVAE對輸出$y$的分佈進行建模。將HB資料y輸入編碼器$q_{\phi_y}(z_y|y)$(圖2左上網路),以預測均值$\mu_{z_y}$和近似後驗分佈$q_{\phi_y}(z_y|y)$的log-variance(對數方差)$\log (\sigma _{z_y}^2)$。然後使用預測的引數通過reparameterization trick(重新引數化技巧)獲得輸出變數$y$的潛在表示$z_y\sim q_{\phi _y}(z_y|y)$(見3.2節)。然後,利用潛在變數$z_x\sim q_{\phi _x}(z_x|x)$作為CVAE condition(條件)變數。串聯後,$z_x$和$z_y$輸入解碼器$p_{\theta_y}(y|z_x,z_y)$(右上的網路),為了預測輸出變數$y$的均值$\mu _y=\mu (z_x,z_y)$。最後,對整個網路進行訓練,共同學習引數$\phi _x$、$\phi _y$和$\theta _y$。由式(3)、(4)可得優化下等價變分下界為:
$$公式5:\log p_{\theta}(y|z_x)\geq L(\theta_y,\phi _y,\phi _x;z_x,y)=-[D_{KL}[q_{\phi _y}(z_y|y)||p_{\theta_y}(z_y)]+||y-f(z_x,z_y;\theta_y)||^2/\alpha]$$
我們希望,在公式5的優化過程中,對編碼器$q_{\phi_x}(z_x|x)$的引數$\phi_x$進行更新,從而使框架學習生成CVAE輸出$\hat{y}$的編碼資訊的潛在表示形式$z_x$。
最後,利用編碼器$q_{\phi_x}(z_x|x)$(圖2中紅色分量表示)對每個$x$估計他們的潛在表示$z_x$,然後使用聯合向量$z_x$和$y$學習GMM迴歸對映[2]。在ABE估計階段,將DR塊(圖1中的紅色框)由編碼器$q_{\phi_x}(z_x|x)$替代,按照第2節中描述的方式進行估計。注意網路$q_{\phi_x}(z_x|x)$和$p_{\phi_y}(y|z_x,z_y)$一起組成一個DNN,有兩個隨機層$z_x$和$z_y$,這本身可以用於ABE,其中$z_y$是在估計階段從先驗分佈$p_{\theta_y}(z_y)=N(0,I)$中取樣的。然而,本文報道的工作的目的是利用CVAE學習到的潛在表示$z_x$作為ABE的DR技術。目的是保持迴歸模型的計算效率。
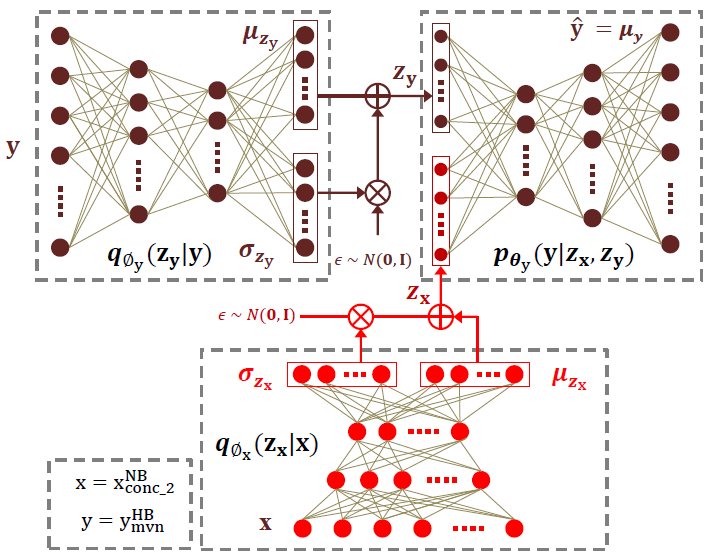
圖2 一種基於CVAE的特徵提取方案
4 實驗設定及結果
本節描述用於ABE實驗的資料集,基線和CVAE配置細節和結果。實驗的目的是比較ABE系統的效能,該系統使用從CVAE中學習到的特性和使用alternative(替代)DR技術的特性。在所有情況下,效能評估均採用或不採用均值和variance normalisation(方差歸一化)。
4.1 資料集
TIMIT資料集[28]用於訓練和驗證。使用3693個來自訓練集的話語和1152個來自測試集(不含核心測試子集)的話語,根據[6]中描述的步驟,並行處理WB和NB語音訊號,來訓練ABE方案。TIMIT core(核心)測試子集(192條語句)用於驗證和網路優化。採用1378個語音組成的The acoustically-different(聽覺不同) TSP資料庫[29]進行測試。將TSP資料下采樣至16kHz,並進行類似的預處理或得並行的WB和NB資料。
4.2 CVAE配置和訓練
CVAE體系結構1是使用Keras toolkit[30]實現的。編碼器$q_{\phi_x}(z_x|x)$和$q_{\phi_y}(z_y|y)$由兩個隱藏層組成,分別為512和256個units(單元),輸入層分別為1000和10個單元。它們的輸出是由均值$\mu_{z_x}$、$\mu_{z_y}$和對數方差$\sigma _{z_x}$、$\sigma _{z_y}$組成的Gaussian-distributed(高斯分佈)的潛在變數層$z_x$和$z_y$,由10個單位組成。解碼器$p_{\theta_x}(x|z_x)$和$p_{\theta_y}(x|z_y)$有2個隱藏層,包含256和512個單元。輸出層分別有1000和10個單元。所有的隱層都有tanh 啟用單元,而高斯引數層有linear 啟用單元。log-variances(對數方差)的建模避免了negative(負)方差的估計。
聯合進行訓練,使用Adam隨機優化技術[31]將公式5的負條件對數似然最小化,初始學習率為10-3,超引數$\beta _1=0.9$,$\beta _2=0.999$並且$\epsilon =10^{-8}$。根據[32]中描述的方法對網路進行初始化,以提高收斂速度。為了防止過度擬合,在每個啟用層之前應用batch-normalisation(批處理規範化)[33]。當驗證損失在連續的5個週期內增加時,學習率降低了一半。首先,VAE對輸入資料x進行50個epoch(週期)的訓練。然後使用輸入x和輸出y資料對full(整個)CVAE進行進一步的50個epoch的訓練。給出最低驗證損失的模型用於後續處理。
將CVAE效能與alternative(選擇)SAE、SSAE和PCA DR技術進行了比較。根據我們之前的工作[15],SSAE和SAE設定有一個共同的結構(512、256、10、256、512)隱藏單元。這些引數是在我們對[15]的研究基礎上選擇的。
4.3 權重因子$\alpha $分析
由於更好地估計HB分量對ABE效能至關重要,因此潛在表示$z_x$應該包含$y$的資訊,因此我們在訓練和測試階段研究了權重因子$\alpha $在reconstruction error(RE)$||y-f(z_y,z_x;\theta_y)||^2$重構誤差上的重要性。
表1顯示了不同的$\alpha $值在epoch結束時的$D_{KL}$和$RE$值,驗證損失最小。$\alpha $值越低,$D_{KL}$值越大,說明approximate posteriorr(近似後驗)$q_{\phi_y}(z_y|y)$與prior先驗分佈$p_{\theta_y}(z_y)=N(0,I)$相差甚遠。這一假設是通過在測試過程中比訓練過程中觀察到更高的REs來證實的。這是因為解碼器$p_{\theta_y}(y|z_x,z_y)$利用測試時從prior(先驗)取樣的潛在變數$z_y$重建輸出$y$,而訓練時從approximate(近似)的posterior(後驗)取樣$z_y$。$\alpha $值越大,$D_{KL}$值越低,說明poatweior distribution(後驗分佈)越接近prior distribution(先驗分佈)。通過對訓練和測試階段相似REs的觀察,證實了這一假設。這些發現證實了之前的工作[20]。根據驗證資料集的REs,本文其餘部分報告的所有實驗都對應於$\alpha =10$的值。
| $\alpha $ | 2 | 5 | 10 | 20 | 30 |
| $D_{KL}$訓練phase(階段) | 0.96 | 0.21 | 3.3e-4 | 1.5e-4 | 9.7e-5 |
| RE訓練階段 | 4.73 | 7.40 | 8.93 | 8.97 | 8.97 |
| RE測試階段 | 11.40 | 9.85 | 8.93 | 8.97 | 8.97 |
圖1 在訓練和測試階段,權重因素對DKL和RE的影響。驗證資料集的結果顯示
4.4 客觀評價
客觀頻譜失真測量包括:均方根對數頻譜失真(RMS-LSD)、所謂的COSH測度(symmetric version(對稱版)的Ikatura-Saito失真)[34]計算的頻率範圍為3.4-8kHz,並將WB擴充套件到感知評價語音質量演算法[35]。後者給出了平均意見得分的客觀估計(MOS-LQOWB)。
結果見表2。PCA降維後的ABE效能優於SAE和VAE技術,說明了在特徵提取過程中進行監督學習或所謂的discriminative fine tunig(判別微調)的重要性。MVN在降低PCA ABE系統性能的同時,顯著提高了SAE和SSAE技術的效能。CVAE ABE系統是所有系統中效能最好的,有趣的是,無論有沒有MVN,效能都是穩定的。這可能是由於潛在表示的概率學習。
| DR方法 | $d_{RMS-LSD(db)}$(db) | $d_{COSH(db)}$ | MOS-LQOWB |
|
PCA PCA+MVN |
6.95 7.35 |
1.43 1.45 |
3.21 3.14 |
|
SAE SAE+MVN |
12.45 7.54 |
2.96 1.50 |
1.95 3.03 |
|
VAE VAE+MVN |
8.64 8.60 |
1.67 1.67 |
2.75 2.75 |
|
SSAE SSAE+MVN |
10.50 6.80 |
2011 1.34 |
2.26 3.28 |
|
CVAE CVAE+MVN |
6.59 6.69 |
1.31 1.30 |
3.34 3.31 |
表2 客觀的評估結果。RMS-LSD和$d_{COSH}$是$dB$中的距離度量(數值越低表示效能越好),而MOS-LQOWB值反映質量(數值越大表示效能越好)
4.5 主觀評價
表3以comparison mean-opinion score(比較平均意見評分,CMOS)的形式展示了比較主觀聽力測試的結果。測試由15名聽眾進行,他們被要求比較使用DT 770 PRO耳機收聽的12對語音訊號A和B的質量。他們被要求在-3(更差)到3(更好)的範圍內對訊號A相對於B的質量進行評級,評分步驟為1。所有用於主觀測試的語音檔案都線上提供2。
| 比較comparison A-->B | CMOS |
|
CVAE-->NB CVAE-->PCA CVAE-->SSAE+MVN CVAE-->WB |
0.90 0.13 0.10 -0.96 |
表3 採用CVAE、SSAE + MVN和PCA DR技術對ABE系統的CMOS進行主觀評價。
使用CVAE方法擴充套件頻寬的語音檔案質量優於原始NB訊號(CMOS為0.90),但仍低於原始WB訊號(CMOS為-0.96)。但是,CVAE系統的語音質量要優於CMOS分別為0.13和0.10的其他系統。
5 總結
條件變分自動編碼器(CVAE)是用於生成模型的有向圖形模型。本文首次將其應用於計算高效的人工頻寬擴充套件(ABE)中的降維。當與標準的ABE迴歸模型一起使用時,使用該方法生成的概率潛在表示不需要任何後處理,如均值和方差歸一化。本文所報道的ABE系統產生的語音質量顯著提高,這一結果得到了客觀評價和主觀評價的證實。改進的原因是利用CVAE對高維譜系數進行了更好的建模。至關重要的是,它們是在不增加回歸模型複雜性的情況下實現的。未來的工作應該將CVAEs與其他生成模型(如對抗性網路)進行比較或結合。
6 參考文獻
[1] S. Li, S. Villette, P. Ramadas, and D. J. Sinder, “Speech bandwidth extension using generative adversarial networks,” in 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2018, pp. 5029–5033.
[2] K.-Y. Park and H. Kim, “Narrowband to wideband conversion of speech using GMM based transformation,” in Proc. of IEEE Int. Conf. on Acoustics, Speech, and Signal Processing(ICASSP), 2000, pp. 1843–1846.
[3] P. Jax and P. Vary, “On artificial bandwidth extension of telephone speech,” Signal Processing, vol. 83, no. 8, pp. 1707–1719, 2003.
[4] K. Li and C.-H. Lee, “A deep neural network approach to speech bandwidth expansion,” in Proc. of IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), 2015, pp.4395–4399.
[5] R. Peharz, G. Kapeller, P. Mowlaee, and F. Pernkopf, “Modeling speech with sum-product networks: Application to bandwidth extension,” in Proc. of IEEE Int. Conf. on Acoustics,Speech and Signal Processing, 2014, pp. 3699–3703.
[6] P. Bachhav, M. Todisco, M. Mossi, C. Beaugeant, and N.Evans, “Artificial bandwidth extension using the constant Qtransform,” in Proc. of IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), 2017, pp. 5550–5554.
[7] I. Katsir, D. Malah, and I. Cohen, “Evaluation of a speech bandwidth extension algorithm based on vocal tract shape estimation,” in Proc. of Int. Workshop on Acoustic Signal Enhancement (IWAENC). VDE, 2012, pp. 1–4.
[8] Y. Gu, Z.-H. Ling, and L.-R. Dai, “Speech bandwidth extension using bottleneck features and deep recurrent neural networks.,” in Proc. of INTERSPEECH, 2016, pp. 297–301.
[9] Y. Wang, S. Zhao, J. Li, J. Kuang, and Q. Zhu, “Recurrent neural network for spectral mapping in speech bandwidth extension,” in Proc. of IEEE Global Conf. on Signal and Information Processing (GlobalSIP), 2016, pp. 242–246.
[10] B. Liu, J. Tao, Z.Wen, Y. Li, and D. Bukhari, “A novel method of artificial bandwidth extension using deep architecture,” in Sixteenth Annual Conf. of the Int. Speech Communication Association,2015.
[11] J. Abel, M. Strake, and T. Fingscheidt, “Artificial bandwidth extension using deep neural networks for spectral envelope estimation,” in Proc. of Int. Workshop on Acoustic Signal Enhancement (IWAENC). IEEE, 2016, pp. 1–5.
[12] A. Nour-Eldin and P. Kabal, “Objective analysis of the effect of memory inclusion on bandwidth extension of narrowband speech,” in Proc. of INTERSPEECH, 2007, pp. 2489–2492.
[13] A. Nour-Eldin, “Quantifying and exploiting speech memory for the improvement of narrowband speech bandwidth extension,” Ph.D. Thesis, McGill University, Canada, 2013.
[14] P. Bachhav, M. Todisco, and N. Evans, “Exploiting explicit memory inclusion for artificial bandwidth extension,” in Proc.of IEEE Int. Conf. on Acoustics, Speech and Signal Processing(ICASSP), 2018, pp. 5459–5463.
[15] P. Bachhav, M. Todisco, and N. Evans, “Artificial bandwidth extension with memory inclusion using semi-supervised stacked auto-encoders,” in Proc. of INTERSPEECH, 2018, pp.1185–1189.
[16] D. Kingma et al., “Semi-supervised learning with deep generative models,” in Advances in Neural Information Processing Systems, 2014, pp. 3581–3589.
[17] K. Sohn, H. Lee, and X. Yan, “Learning structured output representation using deep conditional generative models,” in Advances in Neural Information Processing Systems, 2015,pp.3483–3491.
[18] X. Yan, J. Yang, K. Sohn, and H. Lee, “Attribute2image: Conditional image generation from visual attributes,” in European Conference on Computer Vision. Springer, 2016, pp. 776–791.
[19] W.-N. Hsu, Y. Zhang, and J. Glass, “Learning latent representations for speech generation and transformation,” INTERSPEECH,2017.
[20] M. Blaauw and J. Bonada, “Modeling and transforming speech using variational autoencoders.,” in INTERSPEECH, 2016, pp.1770–1774.
[21] C.-C. Hsu et al., “Voice conversion from non-parallel corpora using variational auto-encoder,” in Signal and Information Processing Association Annual Summit and Conference (APSIPA),2016 Asia-Pacific. IEEE, 2016, pp. 1–6.
[22] K. Akuzawa, Y. Iwasawa, and Y. Matsuo, “Expressive speechsynthesis via modeling expressions with variational autoencoder,” INTERSPEECH, 2018.
[23] Y. Jung, Y. Kim, Y. Choi, and H. Kim, “Joint learning using denoising variational autoencoders for voice activity detection,”Proc. Interspeech 2018, pp. 1210–1214, 2018.
[24] S. Latif, R. Rana, J. Qadir, and J. Epps, “Variational autoencoders for learning latent representations of speech emotion,”INTERSPEECH, 2018.
[25] L. Pandey, A. Kumar, and V. Namboodiri, “Monoaural audio source separation using variational autoencoders,” Proc. Interspeech 2018, pp. 3489–3493, 2018.
[26] D. Kingma and M. Welling, “Auto-encoding variational bayes,” arXiv preprint arXiv:1312.6114, 2013.
[27] C. Doersch, “Tutorial on variational autoencoders,” arXiv preprint arXiv:1606.05908, 2016.
[28] J. Garofolo, L. Lamel, W. Fisher, J. Fiscus, and D. Pallett, “DARPA TIMIT acoustic-phonetic continous speech corpus CD-ROM. NIST speech disc 1-1.1,” NASA STI/Recon technical report N, vol. 93, 1993.
[29] P. Kabal, “TSP speech database,” McGill University, Database Version : 1.0, pp. 02–10, 2002.
[30] F. Chollet et al., “Keras,” https://github.com/keras-team/keras, 2015.
[31] D. Kingma and J. Ba, “Adam: A method for stochastic optimization,”arXiv preprint arXiv:1412.6980, 2014.
[32] K. He et al., “Delving deep into rectifiers: Surpassing humanlevel performance on imagenet classification,” in Proc. of the IEEE int. conf. on computer vision, 2015, pp. 1026–1034.
[33] S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Int. conf. on machine learning, 2015, pp. 448–456.
[34] R. Gray, A. Buzo, A. Gray, and Y. Matsuyama, “Distortion measures for speech processing,” IEEE Trans. on Acoustics,Speech, and Signal Processing, vol. 28, no. 4, pp. 367–376,1980.
[35] “ITU-T Recommendation P.862.2 : Wideband extension to Recommendation P.862 for the assessment of wideband telephone networks and speech codecs,” ITU, 2005.
&n
