二叉查詢樹

　　二叉查詢樹，也稱二叉搜尋樹，或二叉排序樹。其定義也比較簡單，要麼是一顆空樹，要麼就是具有如下性質的二叉樹：

（1）若任意節點的左子樹不空，則左子樹上所有結點的值均小於它的根結點的值；

（2） 若任意節點的右子樹不空，則右子樹上所有結點的值均大於它的根結點的值；

（3） 任意節點的左、右子樹也分別為二叉查詢樹；

（4） 沒有鍵值相等的節點。

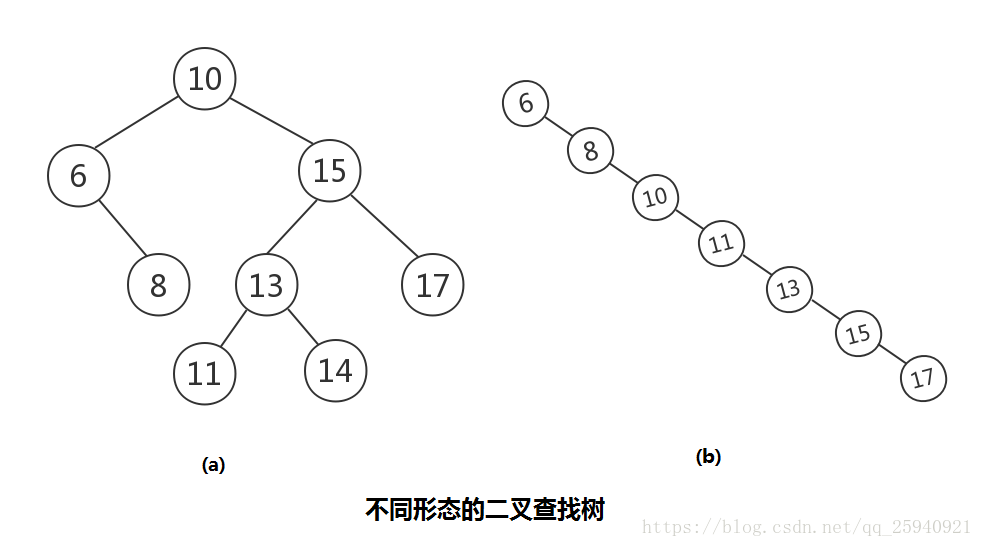
　　如上圖所示，是不同形態的二叉查詢樹。二叉查詢樹是對要查詢的資料進行生成樹，左支的值小於右支的值。在查詢的時候也是一樣的思路，從根節點開始，比節點大進入右支，比節點小進入左支，直到查詢到目標值。

　　二叉查詢樹的插入演算法比較簡單：空樹，就首先生成根節點；不是空樹就按照查詢的演算法，找到父節點，然後作為葉子節點插入，如果值已經存在就插入失敗。

　　刪除操作稍微複雜一點，有如下幾種情況：

​ （1）如果刪除的是葉節點，可以直接刪除；

​ （2）如果被刪除的元素有一個子節點，可以將子節點直接移到被刪除元素的位置；

​ （3）如果有兩個子節點，這時候就採用中序遍歷，找到待刪除的節點的後繼節點，將其與待刪除的節點互換，此時待刪除節點的位置已經是葉子節點，可以直接刪除。如下圖：

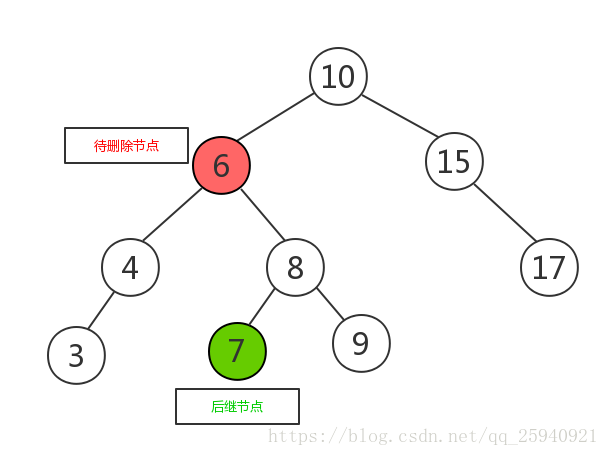
將待刪除節點與後繼節點互換，變成如下圖所示：

將待刪除元素刪除，如下圖所示：

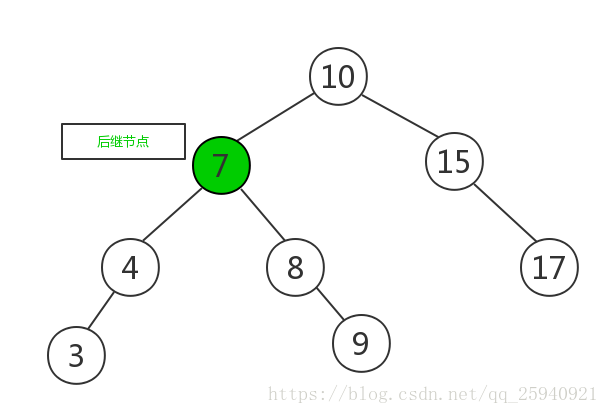
　　另外，二叉查詢樹還有一個性質，即對二叉查詢樹進行中序遍歷，即可得到有序的數列。

​　　二叉查詢樹的查詢複雜度，和二分查詢一樣，插入和查詢的時間複雜度均為 O(logn) ，但是在最壞的情況下仍然會有 O(n) 的時間複雜度。原因在於插入和刪除元素的時候，樹沒有保持平衡（如上不同形態的二叉樹圖中的b）。

平衡二叉樹

​　　平衡二叉搜尋樹，又被稱為AVL樹，且具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。 —-來自百度百科

​　　由於普通的二叉查詢樹會容易失去”平衡“，極端情況下，二叉查詢樹會退化成線性的連結串列，導致插入和查詢的複雜度下降到 O(n) ，所以，這也是平衡二叉樹設計的初衷。那麼平衡二叉樹如何保持”平衡“呢？根據定義，有兩個重點，一是左右兩子樹的高度差的絕對值不能超過1，二是左右兩子樹也是一顆平衡二叉樹。

　　如下圖所示，左圖是一棵平衡二叉樹，根節點10，左右兩子樹的高度差是1，而右圖，雖然根節點左右兩子樹高度差是0，但是右子樹15的左右子樹高度差為2，不符合定義，所以右圖不是一棵平衡二叉樹。

​　　由此可以看出平衡二叉樹是一棵高度平衡的二叉查詢樹。所以，要構建跟維繫一棵平衡二叉樹就比普通的二叉樹要複雜的多。在構建一棵平衡二叉樹的過程中，當有新的節點要插入時，檢查是否因插入後而破壞了樹的平衡，如果是，則需要做旋轉去改變樹的結構。

　　關於旋轉，這東西不拿動態圖將還真很難講明白。所以我就借一下 最容易懂得紅黑樹 這篇文章中左旋右旋的圖來講。

​ 左旋：

​

​ 右旋：

　　不同於順時針跟逆時針變換這種方式去記憶，上面兩個動態圖特別方便記憶跟理解：

　　左旋就是將節點的右支往左拉，右子節點變成父節點，並把晉升之後多餘的左子節點出讓給降級節點的右子節點；

　　而右旋就是反過來，將節點的左支往右拉，左子節點變成了父節點，並把晉升之後多餘的右子節點出讓給降級節點的左子節點。

　　即左旋就是往左變換，右旋就是往右變換。不管是左旋還是右旋，旋轉的目的都是將節點多的一支出讓節點給另一個節點少的一支。

​　　舉個例子，像上圖是否平衡二叉樹的圖裡面，左圖在沒插入前”19“節點前，該樹還是平衡二叉樹，但是在插入”19“後，導致了”15“的左右子樹失去了”平衡“，所以此時可以將”15“節點進行左旋，讓”15“自身把節點出讓給”17“作為”17“的左樹，使得”17“節點左右子樹平衡，而”15“節點沒有子樹，左右也平衡了。如下圖，

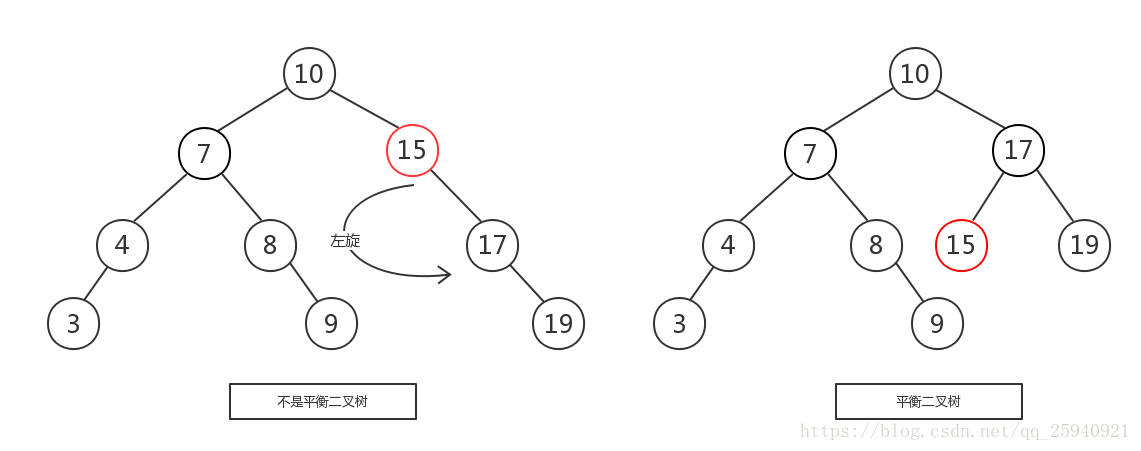
　　由於在構建平衡二叉樹的時候，當有新節點插入時，都會判斷插入後時候平衡，這說明了插入新節點前，都是平衡的，也即高度差絕對值不會超過1。當新節點插入後，有可能會有導致樹不平衡，這時候就需要進行調整，而可能出現的情況就有4種，分別稱作左左，左右，右左，右右。

左左：

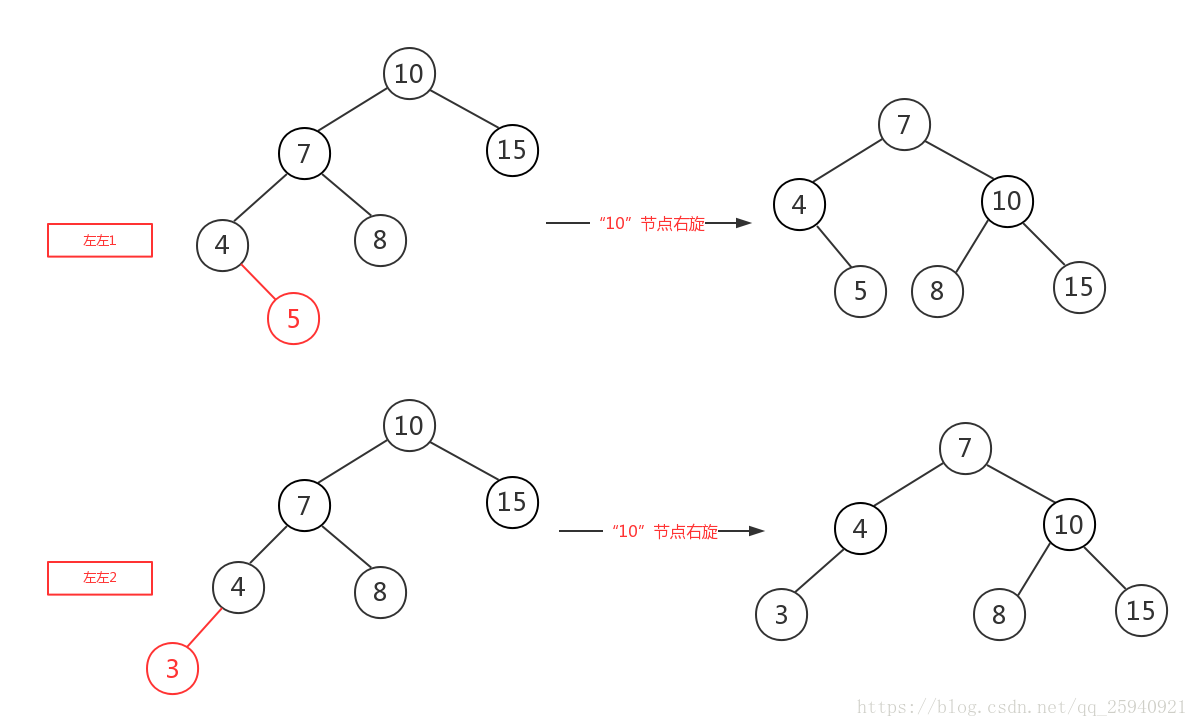
　　左左即為在原來平衡的二叉樹上，在節點的左子樹的左子樹下，有新節點插入，導致節點的左右子樹的高度差為2，如上即為”10“節點的左子樹”7“，的左子樹”4“，插入了節點”5“或”3“導致失衡。

​　　左左調整其實比較簡單，只需要對節點進行右旋即可，如下圖，對節點”10“進行右旋，

　　注意：如果對左右旋變換還不是很懂或不是很熟練的，可以對照著前面的那兩個動圖去想象，自己動手變換幾次，就明白了。

左右：

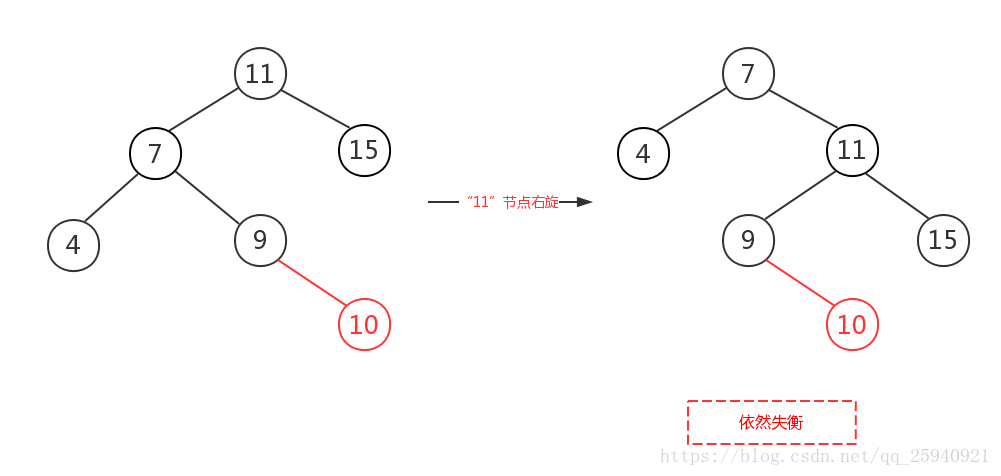
　　左右即為在原來平衡的二叉樹上，在節點的左子樹的右子樹下，有新節點插入，導致節點的左右子樹的高度差為2，如上即為”11“節點的左子樹”7“，的右子樹”9“，插入了節點”10“或”8“導致失衡。

　　左右的調整就不能像左左一樣，進行一次旋轉就完成調整。我們不妨先試著讓左右像左左一樣對”11“節點進行右旋，結果圖如下，右圖的二叉樹依然不平衡，而右圖就是接下來要講的右左，即左右跟右左互為映象，左左跟右右也互為映象。

　　右右跟左左一樣，只需要旋轉一次就能把樹調整平衡，而左右跟右左也一樣，都要進行旋轉兩次才能把樹調整平衡，所以，首先上圖的這種調整是錯誤的，正確的調整方式是，將左右進行第一次旋轉，將左右先調整成左左，然後再對左左進行調整，從而使得二叉樹平衡。

​　　即先對上圖的節點”7“進行左旋，使得二叉樹變成了左左，之後再對”11“節點進行右旋，此時二叉樹就調整完成，如下圖，

右左：

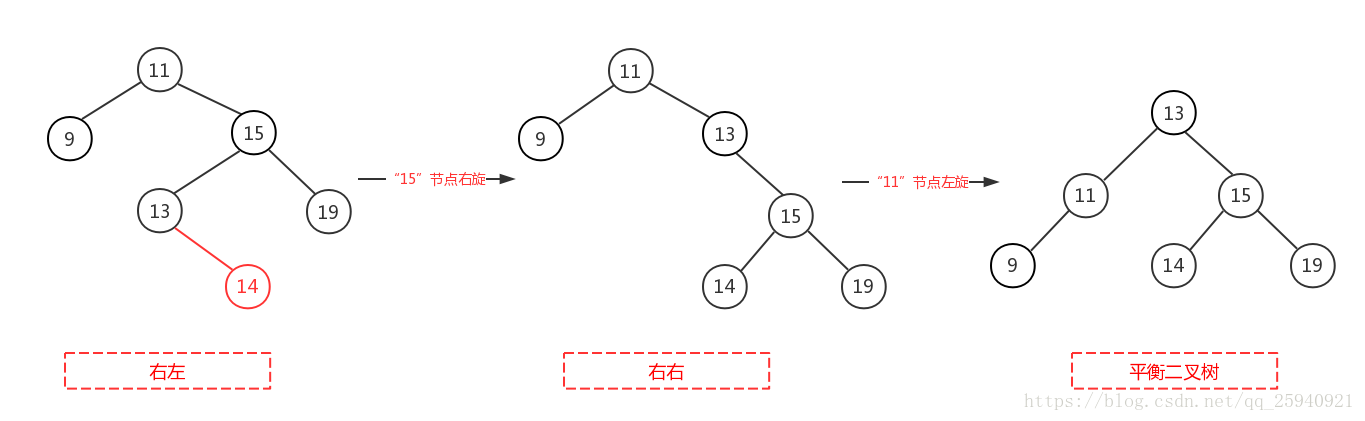
​　　右左即為在原來平衡的二叉樹上，在節點的右子樹的左子樹下，有新節點插入，導致節點的左右子樹的高度差為2，如上即為”11“節點的右子樹”15“，的左子樹”13“，插入了節點”12“或”14“導致失衡。

​　　前面也說了，右左跟左右其實互為映象，所以調整過程就反過來，先對節點”15“進行右旋，使得二叉樹變成右右，之後再對”11“節點進行左旋，此時二叉樹就調整完成，如下圖，

右右：

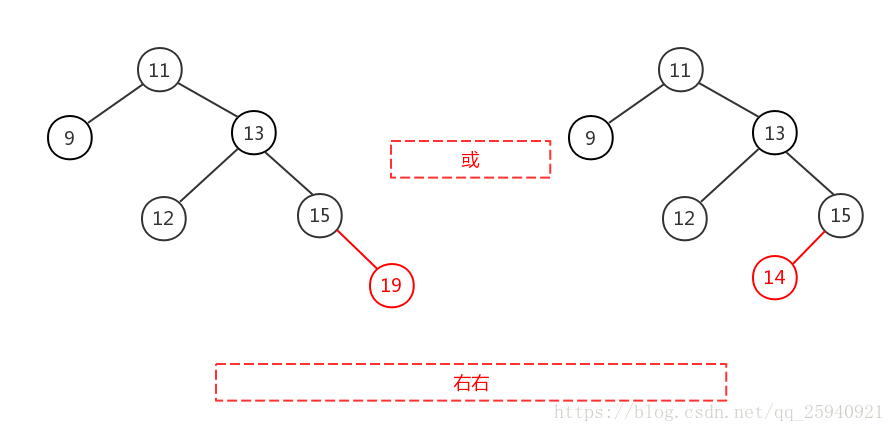
　　右右即為在原來平衡的二叉樹上，在節點的右子樹的右子樹下，有新節點插入，導致節點的左右子樹的高度差為2，如上即為”11“節點的右子樹”13“，的左子樹”15“，插入了節點”14“或”19“導致失衡。

　　右右只需對節點進行一次左旋即可調整平衡，如下圖，對”11“節點進行左旋。

​　　平衡二叉樹構建的過程，就是節點插入的過程，插入失衡情況就上面4種，算簡單了，下面講下平衡二叉樹節點的刪除，刪除的情況會複雜一點，複雜的原因主要在於刪除了節點之後要維繫二叉樹的平衡，但是刪除二叉樹節點總結起來就兩個判斷：①刪除的是什麼型別的節點？②刪除了節點之後是否導致失衡？

　　節點的型別有三種：1.葉子節點；2.只有左子樹或只有右子樹；3.既有左子樹又有右子樹。

​　　針對這三種節點型別，再引入判斷②，所以處理思路分別是：

（1）當刪除的節點是葉子節點，則將節點刪除，然後從父節點開始，判斷是否失衡，如果沒有失衡，則再判斷父節點的父節點是否失衡，直到根節點，此時到根節點還發現沒有失衡，則說此時樹是平衡的；如果中間過程發現失衡，則判斷屬於哪種型別的失衡（左左，左右，右左，右右），然後進行調整。

（2）刪除的節點只有左子樹或只有右子樹，這種情況其實就比刪除葉子節點的步驟多一步，就是將節點刪除，然後把僅有一支的左子樹或右子樹替代原有結點的位置，後面的步驟就一樣了，從父節點開始，判斷是否失衡，如果沒有失衡，則再判斷父節點的父節點是否失衡，直到根節點，如果中間過程發現失衡，則根據失衡的型別進行調整。

（3）刪除的節點既有左子樹又有右子樹，這種情況又比上面這種多一步，就是中序遍歷，找到待刪除節點的前驅或者後驅都行，然後與待刪除節點互換位置，然後把待刪除的節點刪掉，後面的步驟也是一樣，判斷是否失衡，然後根據失衡型別進行調整。

　　最後總結一下，平衡二叉樹是一棵高度平衡的二叉樹，所以查詢的時間複雜度是 O(logN) 。插入的話上面也說，失衡的情況有4種，左左，左右，右左，右右，即一旦插入新節點導致失衡需要調整，最多也只要旋轉2次，所以，插入複雜度是 O(1) ，但是平衡二叉樹也不是完美的，也有缺點，從上面刪除處理思路中也可以看到，就是刪除節點時有可能因為失衡，導致需要從刪除節點的父節點開始，不斷的回溯到根節點，如果這棵平衡二叉樹很高的話，那中間就要判斷很多個節點。所以後來也出現了綜合性能比其更好的樹—-紅黑樹，後面再講。
————————————————
版權宣告：本文為CSDN博主「金髮只是水一下」的原創文章，遵循 CC 4.0 BY-SA 版權協議，轉載請附上原文出處連結及本宣告。
原文連結：https://blog.csdn.net/qq_25940921/article/details/82183