資料分析的入門思維，首先要認識資料，然後對資料進行簡單的分析，比如描述性統計分析和相關性分析等。

一，認識變數和資料

變數和資料是資料分析中常用的概念，用變數來描述事物的特徵，而資料是變數的具體值，把變數的值也叫做觀測值。

1，變數

變數是用來描述總體中成員的某一個特性，例如，性別、年齡、身高、收入等。

變數可以分為：

• 定性變數：用於分類，一般是文字，例如，性別、顏色
• 定序變數：用於表示等級或次序的變數，例如，學歷，職位，排名等，變數的值可以把事務排列為高低或大小，但是各個變數值之間沒有確切的間隔距離，無法確定兩個定序變數之間相差多少。
• 定量變數：是數量變數，能夠比較大小。分為兩類：離散變數和連續變數。

2，資料

資料是變數的具體值，按照變數的型別，可以把資料分為：分類資料、順序資料和數值型資料。

按照資料分析的目的，可以把資料分為實驗組（Treatment）和參照組（Control）。

按照資料的型別，可以把資料分為：文字資料、數值型資料和日期時間資料。

3，缺失值

不是所有的資料都是完整的，有些觀測值可能會缺失，對於缺失值，通常的處理方式是：刪除缺失值所在的資料行，填充缺失值、插補缺失值。

4，觀測值的重編碼

資料分析中，通常需要把連續型變數轉換為定序變數，例如，把學生的成績劃分為優秀、良好、合格和差4個等級，這種操作也稱作離散化。

當觀測資料所用的單位可能影響資料分析時，還需要對資料進行規範化，常用的規範化方法是：最小-最大規範化，標準化變換等。

觀測值的重編碼，後續會有詳細的介紹。

二，描述性統計分析

描述性統計量分為：集中趨勢、離散程度（離中趨勢）和分佈形態。

1，集中趨勢的描述性統計量

• 均值：是指一組資料的算術平均數，描述一組資料的平均水平，是集中趨勢中波動最小、最可靠的指標，但是均值容易受到極端值（極小值或極大值）的影響。
• 中位數：是指當一組資料按照順序排列後，位於中間位置的數，不受極端值的影響，對於定序型變數，中位數是最適合的表徵集中趨勢的指標。
• 眾數：是指一組資料中出現次數最多的觀測值，不受極端值的影響，常用於描述定性資料的集中趨勢。

2，離散程度的描述性統計量

• 最大值和最小值：是一組資料中的最大觀測值和最小觀測值
• 極差：又稱全距，是一組資料中的最大觀測值和最小觀測值之差，記作R，一般情況下，極差越大，離散程度越大，其值容易受到極端值的影響。
• 方差和標準差：是描述一組資料離散程度的最常用、最適用的指標，值越大，表明資料的離散程度越大。

3，分佈形態的描述性統計量

偏度：用來評估一組資料的分佈呈先的對稱程度，當偏度=0時，分佈是對稱的；當偏度>0時，分佈呈正偏態；當偏度<0時，分佈呈負偏態。

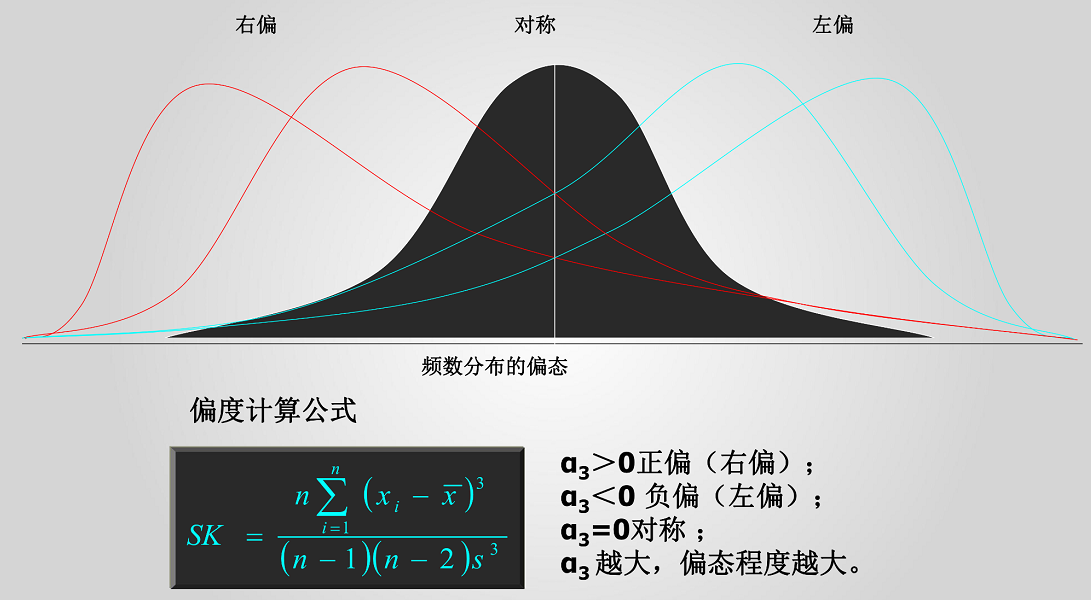
峰度：用來評估一組資料的分佈形狀的高低程度的指標，當峰度=0時，分佈和正態分佈基本一直；當峰度>0時，分佈形態高狹；當峰度<0時，分佈形態低闊。

4，頻率分析

頻數分佈分析（又稱頻率分析）主要通過頻數分佈表、條形圖和直方圖、百分位值等來描述資料的分佈特徵。

在做頻數分佈分析時，通常按照定性資料（即分類的類別），統計各個分類的頻數，計算各個分類所佔的百分比，進而得到頻率分佈表，最後根據頻率分佈表來繪製頻率分佈圖。

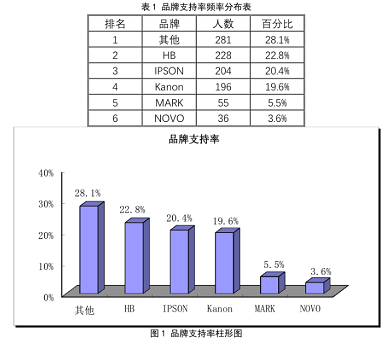
5，按照時間遞增的趨勢分析

特殊情況下，當X軸是日期資料，Y軸是統計量（比如均值、總數量）時，可以繪製出統計量按照時間遞增的趨勢圖，從圖中可以看到統計量按照時間增加的趨勢（無變化、遞增或遞減）和週期性。

例如，下圖的X軸是日期，Y軸的統計量是總數量，兩條折線分別是湖北確診病例人數和湖北新增確診病例人數：

三，相關性分析 

相關性分析是研究事務之間是否存在某種依存關係，並對具有依存關係的現象進行相關方向和相關程度的分析。

相關程度用相關係數r表示，|r|<=1，r=0表示不相關，通常情況下，0 < | r | <1表示變數之間存在不同程度的線性相關，根據約定的規則：

• | r | <=0.3 ：為弱線性相關或不存線上性相關；
• 0.3 < | r | <=0.5 ：低度線性相關，認為存線上性相關，但是相關性不明顯
• 0.5 < | r | <=0.8 ：顯著線性相關，認為存在強線性相關，存在明顯的相關性
• | r | >0.8 ：高度相關，認為存在極強的線性相關

參考文