Python神經網路程式設計筆記
神經元
想一想便知道,當一個人捏你一下以至於你會痛得叫起來的力度便是神經元的閾值,而我們構建的時候也是把這種現象抽象成一個函式,叫作啟用函式。
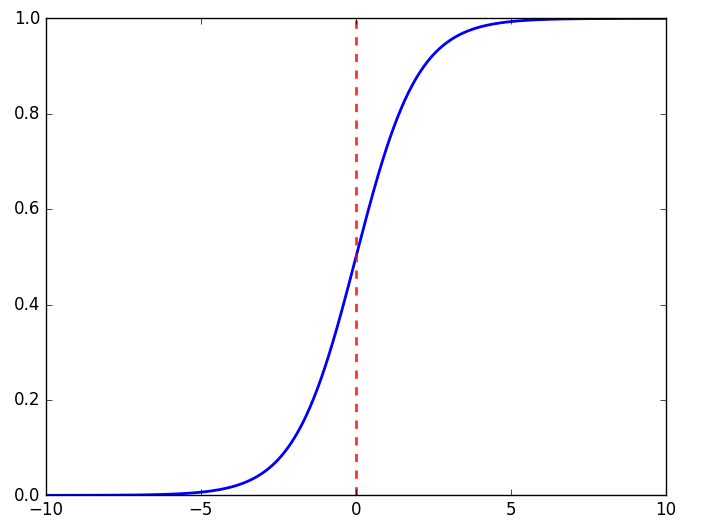
而這裡便是我們使用sigmoid函式的原因,它是一個很簡單的函式,平滑更接近顯示。
\[y=\frac{1}{1+e^{-x}}\]
神經網路傳遞訊號
神經網路便是通過一個一個神經元連線,使用權值x輸入的和在通過sigmoid函式得到最終的輸出值,然後一層一層的傳遞下去。
\[O = sigmoid(W\cdot I)\]
其中,\(O\)為輸出矩陣,\(W\)為權值矩陣,\(I\)為輸入矩陣。
舉個栗子:
假設我們設定一個三層神經網路,分別為輸入層,隱藏層(注意:不管我們中間有多少層,中間的都叫隱藏層,我們這裡隱藏層只有一層),輸出層。
1.輸入層->隱藏層:我們輸入矩陣是一個(3x1)的矩陣,那麼我們設定四個權值,那麼我們的第一個權值矩陣(就是輸入層->隱藏層的)的維度也就為(4x3),這時我們相乘也就得到輸出矩陣(4x1),進行下一步時,這個(4x1)的輸出矩陣就變成了輸入;
2.隱藏層->輸出層:這是我們的輸入矩陣是一個(4x1)的矩陣,然後我們要求輸出層輸出為兩個值,那麼我們第二個權值矩陣(就是隱藏層->輸出層的)的維度也就為(2x4),這時我們相乘也就得到輸出矩陣(2x1),也就為最終的結果了。
反向傳播
現在我們已經可以收到由前面的層傳輸過來的結果了,但答案肯定是不準的,那麼我們該如何進行改進呢?
毫無疑問,首先我們要計算誤差,假設真實值為t,輸出值為o,那麼誤差e就為:
\[e=t-o\]
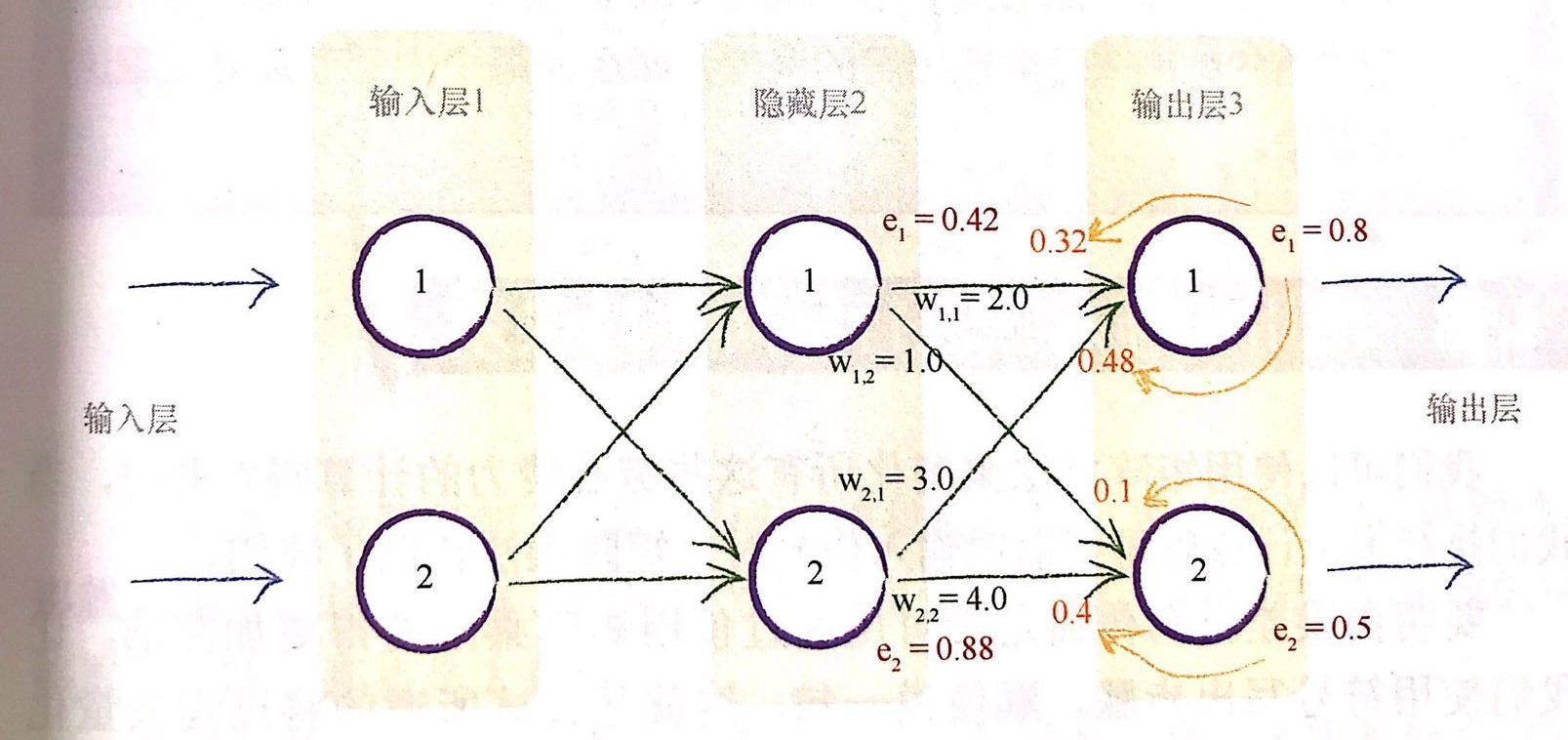
我們按照上圖來進行舉例說明。
1.更新誤差
那麼,隱藏層的誤差如何確定呢?
我們使用連結\(w_{1,1}\)和連結\(w_{2,1}\)上的分割誤差之和來進行更新,也就是
\[e_{hidden,1}=e_{output,1}*\frac{w_{1,1}}{w_{1,1}+w_{2,1}}+e_{output,2}*\frac{w_{1,2}}{w_{1,2}+w_{2,2}}\]
我們也進行帶值進行計算
\[0.8*\frac{2}{2+3}+0.5*\frac{1}{1+4}=0.42\]
2.使用矩陣進行更新
我們發現上面的公式應用到矩陣運算會很複雜,我們究其本質,最重要的事情是輸出誤差與連結權重\(w_{ij}\)的乘法。較大的權重就意味著攜帶較多的輸出誤差給隱藏層,這些分數的分母是一種歸一化因子。如果我們忽略這種因子,那麼我們僅僅失去後潰誤差的大小。
也就是這裡我們使用\(e_1*w_{1,1}\)來代替\(e_1*w_{1,1}/(w_{1,1}+w_{2,1})\) 。那麼我們就可以很容易的進行矩陣運算進行誤差更新了。
\[error_{hidden}=w^T_{hidden\_output}\cdot error_{output}\]
3.更新權重
在神經網路中,我們採用梯度下降法來尋找最優的權重值。神經網路本身的輸出函式部署一個誤差函式,但我們知道,由於誤差是目標訓練值與實際輸出值之間的差值,因此我們可以很容易的構建誤差函式,即
\[(目標值-實際值)^2\]
為什麼我們要構建平方項呢?為何不用絕對值誤差呢?原因有三
- 使用誤差的平方,我們可以很容易的使用代數計算出梯度下降的斜率;
- 誤差函式平滑連續,這是的梯度下降法很好地發揮作用,沒有間斷,也沒有突然的跳躍;
- 越接近最小值,梯度越小,這意味著,如果我們使用這個函式調節步長,超調的風險就會變得很小。
現在我們要更新\(w_{j,k}\)的權值,那麼來推導一下它的更新公式:
首先有
\[\frac{\partial E}{\partial W_{j,k}} = \frac{\partial}{\partial W_{j,k}}(t_k-o_k)^2\]
然後根據鏈式法則得到:
\[\frac{\partial E}{\partial W_{j,k}} = \frac{\partial E}{\partial o_k} \cdot \frac{\partial o_k}{\partial W_{j,k}}\]
然後我們對其求偏導:
\[\frac{\partial E}{\partial W_{j,k}} = -2(t_k-o_k) \cdot \frac{\partial o_k}{\partial W_{j,k}}\\ = -2(t_k-o_k) \cdot \frac{\partial}{\partial W_{j,k}}sigmoid(\sum_{j}w_{j,k}\cdot o_j)\\ = -2(t_k-o_k) \cdot sigmoid(\sum_{j}w_{j,k}\cdot o_j)(1-sigmoid(\sum_{j}w_{j,k}\cdot o_j)) \cdot \frac{\partial}{\partial W_{j,k}}(\sum_{j}w_{j,k}\cdot o_j)\\ = -2(t_k-o_k) \cdot sigmoid(\sum_{j}w_{j,k}\cdot o_j)(1-sigmoid(\sum_{j}w_{j,k}\cdot o_j)) \cdot o_j\]
這樣我們就得到了最後的權重更新公式:
\[new W_{j,k} = oldW_{j,k} - \alpha \cdot \frac{\partial E}{\partial W_{j,k}} \]
其中:
\[\frac{\partial E}{\partial W_{j,k}} = \Delta w_{j,k} = \alpha \cdot E_k \cdot O_k(1-O_k) \cdot O_j^T\]
輸入與輸出
1.輸入
我們觀察sigmoid函式注意到,當輸入值變大,啟用函式也就會越來越平坦,權重的改變取決於啟用函式的梯度,小梯度也就意味著限制了神經網路的學習能力,這就是所謂的飽和神經網路。因此,我們要儘量保持小的輸入。
但有趣的是,當輸入訊號太小,計算機便會損失精度,所以我們要保持輸入範圍在0.0~1.0之間,但輸入為0的話會將\(o_j\)設定為0,這樣的權重更新表示式就會等於0,從而造成學習能力的喪失,我們需要加上一個小小的偏移,例如0.01,避免輸入0帶來的麻煩。
2.輸出
我們使用啟用函式得到的值的範圍會被限制在0~1之間,注意:邏輯函式甚至不能取到1.0,只能接近於1.0.數學家們稱之為漸進於1.0.
因此,我們需要調整目標值,匹配啟用函式的可能輸出,常見的使用範圍為0.0~1.0之間,但我們是取不到0.0和1.0的,所以這裡我們也要進行偏移,例如0.01~0.99.
隨機初始權重
和輸入輸出一樣,初始的權重設定也要遵從同樣地原則。過大的初始權重會造成大的訊號傳遞給啟用函式,導致網路飽和,從而降低學習到更好的權重的能力,因此應該避免大的初始權重值。
我們可以從-1.0~+1.0之間隨機均勻地挑選初始權重。而我們也希望初始權重的分佈是均勻的,經過數學家們的證明,我們有一個比較好的挑選方式,那就是從均值為0、標準方差等於節點傳入連結數量平方根倒數的正態分佈中進行取樣。
總而言之,我們要禁止將初始權重設定為0或者將初始權重設定為像痛得恆定值,這樣會很糟糕。
程式碼實現
import numpy as np
import scipy.special
import matplotlib.pyplot as plt
# neural network class definition
class NeuralNetwork:
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
# set number of nodes in each input, hidden, output layer
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# learning rate
self.lr = learningrate
# 初始權重矩陣
self.wih = np.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
self.who = np.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))
# 啟用函式
self.activation_function = lambda x: scipy.special.expit(x)
pass
def train(self, inputs_list, targets_list):
# 輸入
inputs = np.array(inputs_list, ndmin=2).T
targets = np.array(targets_list, ndmin=2).T
# 隱藏層計算
hidden_inputs = np.dot(self.wih, inputs)
hidden_outputs = self.activation_function(hidden_inputs)
# 輸出層計算
final_inputs = np.dot(self.who, hidden_outputs)
final_outputs = self.activation_function(final_inputs)
# 誤差計算
output_errors = targets - final_outputs
hidden_errors = np.dot(self.who.T, output_errors)
# 反向傳播更新權值
self.who += self.lr * np.dot((output_errors * final_outputs * (1.0 - final_outputs)), np.transpose(hidden_outputs))
self.wih += self.lr * np.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), np.transpose(inputs))
pass
def query(self, inputs_list):
# 輸入
inputs = np.array(inputs_list, ndmin=2).T
# 隱藏層計算
hidden_inputs = np.dot(self.wih, inputs)
hidden_outputs = self.activation_function(hidden_inputs)
# 輸出層計算
final_inputs = np.dot(self.who, hidden_outputs)
final_outputs = self.activation_function(final_inputs)
return final_outputs
if __name__ == '__main__':
input_nodes = 784
hidden_nodes = 200
output_nodes = 10
learning_rate = 0.2
nn = NeuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
# 載入資料
train_data_file = open("./mnist_train.csv", "r")
train_data_list = train_data_file.readlines()
train_data_file.close()
print("資料讀取完畢")
# 視覺化
# all_values = train_data_list[0].split(',')
# image_array = np.asfarray(all_values[1:]).reshape((28, 28))
# plt.imshow(image_array, cmap="Greys", interpolation='None')
# plt.show()
epochs = 2
for e in range(epochs):
print("\t===== epochs %d =====\t" % (e+1))
for record in train_data_list:
all_values = record.split(',')
inputs = (np.asfarray(all_values[1:]) / 255 * 0.99) + 0.01
targets = np.zeros(output_nodes) + 0.01
targets[int(all_values[0])] = 0.99
nn.train(inputs, targets)
# 預測
test_data_file = open("./mnist_test.csv", "r")
test_data_list = test_data_file.readlines()
test_data_file.close()
print(len(test_data_list))
t_num = 0
for line in test_data_list:
all_values = line.split(',')
y = all_values[0]
y_pred = np.argmax(nn.query(np.asfarray(all_values[1:]) / 255 * 0.99 + 0.01))
if int(y) == int(y_pred):
t_num += 1
print(t_num)
print(t_num * 1.0 / len(test_data_list))這份三層神經網路對mnist手寫資料集能達到97%的準確度
