# 1 簡介 ## 1.1 歷史 DES(Data Encryption Standard)是由IBM公司在**1974年提出**的加密演算法，在**1977年被NIST定位資料加密標準**。隨後的很多年裡，DES都是最流行的對稱密碼演算法，尤其是在金融領域更是如此，直到90年代隨著對DES研究的深入和算力的發展，DES變得不再那麼安全，但1994年NIST仍然公佈了DES在未來地5年將繼續作為資料加密標準，到1999年，NIST宣佈DES將只在法律系統中使用並推出了它的改進版3DES，即使用兩個或三個不同的金鑰重複三次DES的操作。直到**2001年，AES（Adanced Encryption Standard）的提出，DES逐漸退出了歷史舞臺**。 這裡簡單提一句，DES的不安全性主要源自於它的**金鑰過短**，只有64位，所以其改進版3DES到今天依然活躍在很多加密系統中。 ## 1.2 結構 DES使用了典型的Feistel結構（見[維基百科]([https://zh.wikipedia.org/zh-hans/%E8%B4%B9%E6%96%AF%E5%A6%A5%E5%AF%86%E7%A0%81](https://zh.wikipedia.org/zh-hans/費斯妥密碼)))，只在開始時添加了一個初始置換和結束時添加了一個逆初始置換。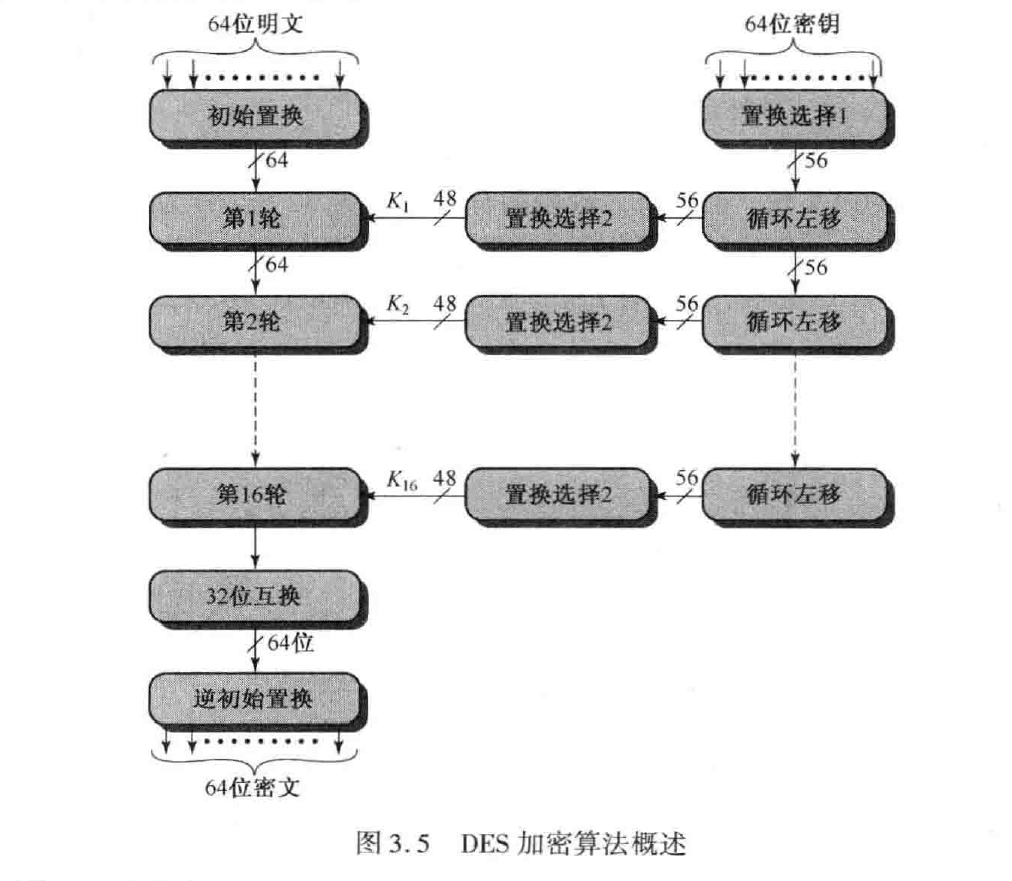 結構圖表示如下：  首先解釋一下上圖，DES共有16輪，對於每個輸入的分組（64bit），首先會進行一次初始置換($IP$)，初始置換後即進行16輪的加密，種子金鑰會為每一輪加密操作生成一個48bit的輪金鑰，具體的生成過程以及為什麼是48bit後邊會有相應的解釋。 對每一輪來說，輸入的資料都被分為左右兩部分，各32bit。每一輪的右半部分成為下一輪的左半部分，而左半部分同經過一系列操作的右半部分異或成為新的右半部分（除16輪）。 16輪加密結束後，會首先進行一次左右部分的互換，再進行一次逆初始置換($IP^{-1}$)就得到了64bit的密文分組，下面我們來詳細介紹每一輪操作具體發生了什麼，以及輪金鑰是如何生成的。 # 2 演算法描述 ## 2.1 $IP,IP^{-1}$ 講內部結構之前先介紹一下初始置換和逆初始置換的具體操作： 其實都是很簡單的根據表換位置的操作，首先是初始置換： | 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 | | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: | | 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 | | 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 | | 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 | | 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 | | 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 | | 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 | | 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 | 即將輸入明文的第58位放到第一位，第50位放到第二位，以此類推， 相應的，逆初始置換就是把要輸出的密文按照表進行置換（我想設定它的原因應該是為了對稱地解密）： | 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 | | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: | | 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 | | 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 | | 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 | | 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 | | 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 | | 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 | | 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 | ## 2.2 輪加密 對每輪操作來說，都是隻需要對輸入資料的右半部分的32bit進行操作。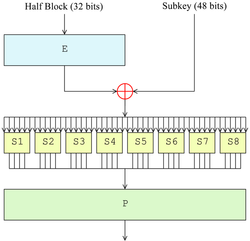每輪加密的內部結構可以用下圖來表示：  - **擴張**：將32bit的右半部分拓張為48bit的值，從下表可以看出，實際上就是以4bit為一組，把原本左右相鄰的bit複製一次，擴張為6*8=48bit | 32 | 1 | 2 | 3 | 4 | 5 | | :--: | :--: | :--: | :--: | :--: | :--: | | 4 | 5 | 6 | 7 | 8 | 9 | | 8 | 9 | 10 | 11 | 12 | 13 | | 12 | 13 | 14 | 15 | 16 | 17 | | 16 | 17 | 18 | 19 | 20 | 21 | | 20 | 21 | 22 | 23 | 24 | 25 | | 24 | 25 | 26 | 27 | 28 | 29 | | 28 | 29 | 30 | 31 | 32 | 1 | - **輪金鑰加**：將拓展置換生成的48bit與輪金鑰異或，輪金鑰同樣是48bit的，輪金鑰如何生成將在下一部分解釋 - **S盒替換**：S盒是DES中最核心的部分，有了S盒DES才具有了非線性的性質，安全性得到保障。S盒將輸入的48bit轉化位32bit的輸出，它的實現細節可以簡述為：S盒共8個，每個S盒可以看作一個4*16的矩陣，將輸入每6bit一組輸入對應的S盒，輸入的第0、5bit組合起來決定行數，中間4bit組合起來決定列數，S盒也是DES中最有爭議的一部分，因為它的設計原則並未公開，被懷疑裝有後門，具體的S盒是這樣規定的： | S1 | | | | | | | | | | | | | | | | | | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | :----: | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 14 | 4 | 13 | 1 | 2 | 15 | 11 | 8 | 3 | 10 | 6 | 12 | 5 | 9 | 0 | 7 | | 0yyyy1 | 0 | 15 | 7 | 4 | 14 | 2 | 13 | 1 | 10 | 6 | 12 | 11 | 9 | 5 | 3 | 8 | | 1yyyy0 | 4 | 1 | 14 | 8 | 13 | 6 | 2 | 11 | 15 | 12 | 9 | 7 | 3 | 10 | 5 | 0 | | 1yyyy1 | 15 | 12 | 8 | 2 | 4 | 9 | 1 | 7 | 5 | 11 | 3 | 14 | 10 | 0 | 6 | 13 | | S2 | | | | | | | | | | | | | | | | | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 15 | 1 | 8 | 14 | 6 | 11 | 3 | 4 | 9 | 7 | 2 | 13 | 12 | 0 | 5 | 10 | | 0yyyy1 | 3 | 13 | 4 | 7 | 15 | 2 | 8 | 14 | 12 | 0 | 1 | 10 | 6 | 9 | 11 | 5 | | 1yyyy0 | 0 | 14 | 7 | 11 | 10 | 4 | 13 | 1 | 5 | 8 | 12 | 6 | 9 | 3 | 2 | 15 | | 1yyyy1 | 13 | 8 | 10 | 1 | 3 | 15 | 4 | 2 | 11 | 6 | 7 | 12 | 0 | 5 | 14 | 9 | | S3 | | | | | | | | | | | | | | | | | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 10 | 0 | 9 | 14 | 6 | 3 | 15 | 5 | 1 | 13 | 12 | 7 | 11 | 4 | 2 | 8 | | 0yyyy1 | 13 | 7 | 0 | 9 | 3 | 4 | 6 | 10 | 2 | 8 | 5 | 14 | 12 | 11 | 15 | 1 | | 1yyyy0 | 13 | 6 | 4 | 9 | 8 | 15 | 3 | 0 | 11 | 1 | 2 | 12 | 5 | 10 | 14 | 7 | | 1yyyy1 | 1 | 10 | 13 | 0 | 6 | 9 | 8 | 7 | 4 | 15 | 14 | 3 | 11 | 5 | 2 | 12 | | S4 | | | | | | | | | | | | | | | | | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 7 | 13 | 14 | 3 | 0 | 6 | 9 | 10 | 1 | 2 | 8 | 5 | 11 | 12 | 4 | 15 | | 0yyyy1 | 13 | 8 | 11 | 5 | 6 | 15 | 0 | 3 | 4 | 7 | 2 | 12 | 1 | 10 | 14 | 9 | | 1yyyy0 | 10 | 6 | 9 | 0 | 12 | 11 | 7 | 13 | 15 | 1 | 3 | 14 | 5 | 2 | 8 | 4 | | 1yyyy1 | 3 | 15 | 0 | 6 | 10 | 1 | 13 | 8 | 9 | 4 | 5 | 11 | 12 | 7 | 2 | 14 | | S5 | | | | | | | | | | | | | | | | | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 2 | 12 | 4 | 1 | 7 | 10 | 11 | 6 | 8 | 5 | 3 | 15 | 13 | 0 | 14 | 9 | | 0yyyy1 | 14 | 11 | 2 | 12 | 4 | 7 | 13 | 1 | 5 | 0 | 15 | 10 | 3 | 9 | 8 | 6 | | 1yyyy0 | 4 | 2 | 1 | 11 | 10 | 13 | 7 | 8 | 15 | 9 | 12 | 5 | 6 | 3 | 0 | 14 | | 1yyyy1 | 11 | 8 | 12 | 7 | 1 | 14 | 2 | 13 | 6 | 15 | 0 | 9 | 10 | 4 | 5 | 3 | | S6 | | | | | | | | | | | | | | | | | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 12 | 1 | 10 | 15 | 9 | 2 | 6 | 8 | 0 | 13 | 3 | 4 | 14 | 7 | 5 | 11 | | 0yyyy1 | 10 | 15 | 4 | 2 | 7 | 12 | 9 | 5 | 6 | 1 | 13 | 14 | 0 | 11 | 3 | 8 | | 1yyyy0 | 9 | 14 | 15 | 5 | 2 | 8 | 12 | 3 | 7 | 0 | 4 | 10 | 1 | 13 | 11 | 6 | | 1yyyy1 | 4 | 3 | 2 | 12 | 9 | 5 | 15 | 10 | 11 | 14 | 1 | 7 | 6 | 0 | 8 | 13 | | S7 | | | | | | | | | | | | | | | | | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 4 | 11 | 2 | 14 | 15 | 0 | 8 | 13 | 3 | 12 | 9 | 7 | 5 | 10 | 6 | 1 | | 0yyyy1 | 13 | 0 | 11 | 7 | 4 | 9 | 1 | 10 | 14 | 3 | 5 | 12 | 2 | 15 | 8 | 6 | | 1yyyy0 | 1 | 4 | 11 | 13 | 12 | 3 | 7 | 14 | 10 | 15 | 6 | 8 | 0 | 5 | 9 | 2 | | 1yyyy1 | 6 | 11 | 13 | 8 | 1 | 4 | 10 | 7 | 9 | 5 | 0 | 15 | 14 | 2 | 3 | 12 | | S8 | | | | | | | | | | | | | | | | | | | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x | | 0yyyy0 | 13 | 2 | 8 | 4 | 6 | 15 | 11 | 1 | 10 | 9 | 3 | 14 | 5 | 0 | 12 | 7 | | 0yyyy1 | 1 | 15 | 13 | 8 | 10 | 3 | 7 | 4 | 12 | 5 | 6 | 11 | 0 | 14 | 9 | 2 | | 1yyyy0 | 7 | 11 | 4 | 1 | 9 | 12 | 14 | 2 | 0 | 6 | 10 | 13 | 15 | 3 | 5 | 8 | | 1yyyy1 | 2 | 1 | 14 | 7 | 4 | 10 | 8 | 13 | 15 | 12 | 9 | 0 | 3 | 5 | 6 | 11 | 例如“**0**1101**1**”的輸入的外側位為“**01**”，內側位為“1101”，即第2行，第14列。因此在S5中的對應輸出為“1001”（十進位制的9） - **P置換**：P置換將S盒輸出的32位資料重新排列 | 16 | 7 | 20 | 21 | | :--: | :--: | :--: | :--: | | 29 | 12 | 28 | 17 | | 1 | 15 | 23 | 26 | | 5 | 18 | 31 | 10 | | 2 | 8 | 24 | 14 | | 32 | 27 | 3 | 9 | | 19 | 13 | 30 | 6 | | 22 | 11 | 4 | 25 | 置換後輸出的資料同本輪的左半部分異或成為新的右半部分，隨即作為輸入進入下一輪。 # 3 輪金鑰生成 上面提到，參與輪金鑰加的輪金鑰有48bit，但種子金鑰是有64bit的，生成輪金鑰主要要經過以下幾步： ## 3.1 選擇置換（PC-1） 在輸入的種子金鑰中，有8bit是不用於加密的，通常用於校驗或者直接捨棄掉，PC-1就是打亂順序的同時捨棄掉這些位元，觀察下表，首先可以注意到表中是沒有8、16、24這些位元的；此外，PC-1結束後金鑰被分為左右兩部分，如下表所示： | 左 | | | | | | | | :--: | :--: | :--: | :--: | :--: | :--: | :--: | | 57 | 49 | 41 | 33 | 25 | 17 | 9 | | 1 | 58 | 50 | 42 | 34 | 26 | 18 | | 10 | 2 | 59 | 51 | 43 | 35 | 27 | | 19 | 11 | 3 | 60 | 52 | 44 | 36 | | 右 | | | | | | | | 63 | 55 | 47 | 39 | 31 | 23 | 15 | | 7 | 62 | 54 | 46 | 38 | 30 | 22 | | 14 | 6 | 61 | 53 | 45 | 37 | 29 | | 21 | 13 | 5 | 28 | 20 | 12 | 4 | # 3.2 迴圈移位 對每一輪操作，金鑰的左右兩部分會同時進行迴圈左移，每一輪迴圈左移的位數規定如下： | 回次 | 左移位數 | | :--: | :------: | | 1 | 1 | | 2 | 1 | | 3 | 2 | | 4 | 2 | | 5 | 2 | | 6 | 2 | | 7 | 2 | | 8 | 2 | | 9 | 1 | | 10 | 2 | | 11 | 2 | | 12 | 2 | | 13 | 2 | | 14 | 2 | | 15 | 2 | | 16 | 1 | ## 3.3 壓縮置換（PC-2） 每一次迴圈左移結束後，根據下表選出48bit作為輪金鑰，所以選擇置換2又被稱為壓縮置換： | 14 | 17 | 11 | 24 | 1 | 5 | | :--: | :--: | :--: | :--: | :--: | :--: | | 3 | 28 | 15 | 6 | 21 | 10 | | 23 | 19 | 12 | 4 | 26 | 8 | | 16 | 7 | 27 | 20 | 13 | 2 | | 41 | 52 | 31 | 37 | 47 | 55 | | 30 | 40 | 51 | 45 | 33 | 48 | | 44 | 49 | 39 | 56 | 34 | 53 | | 46 | 42 | 50 | 36 | 29 | 32 | 這樣，每一輪都能得到一個單獨的輪金鑰用於輪金鑰加的操作。 解密時，只需要將輪金鑰序列反序使用即可 # 4 解密操作 開頭說過，DES時典型的Feistel結構，在直到金鑰的情況下很容易就能實現對稱解密。 最開始學習的時候，收AES的影響，我以為是每個操作都會有一個逆操作，相應的S盒也有一個逆S盒，但在我程式碼實現時我發現這是錯誤的，不像AES是基於有限域上的操作，DES的S盒是沒有逆操作的，這時我才明白，原來只需要一樣的步驟，只需要改變輪金鑰的順序就能實現解密操作，所以說，學習知識時還是要仔細思考，不能淺嘗輒止！ # 參考資料 1. 維基百科[DES](https://zh.wikipedia.org/wiki/資料加密標準) 2. [DES描述 NIST](http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf) 3. 密碼編碼學與網路安全原理與實踐（英文版）