二分搜尋樹(Binary Search Tree)
阿新 • • 發佈:2020-04-04
[TOC]
###什麼是二叉樹?
在實現二分搜尋樹之前,我們先思考一下,為什麼要有樹這種資料結構呢?我們通過企業的組織機構、檔案儲存、資料庫索引等這些常見的應用會發現,將資料使用樹結構儲存後,會出奇的高效,樹結構本身是一種天然的組織結構。常見的樹結構有:二分搜尋樹、平衡二叉樹(常見的平衡二叉樹有AVL和紅黑樹)、堆、並查集、線段樹、Trie等。Trie又叫字典樹或字首樹。
樹和連結串列一樣,都屬於動態資料結構,由於二分搜尋樹是二叉樹的一種,我們先來說說什麼是二叉樹。二叉樹具有唯一的根節點,二叉樹每個節點最多有兩個孩子節點,二叉樹的每個節點最多有一個父親節點,二叉樹具有天然遞迴結構,每個節點的左子數也是一棵二叉樹,每個節點的右子樹也是一顆二叉樹。二叉樹如下圖: 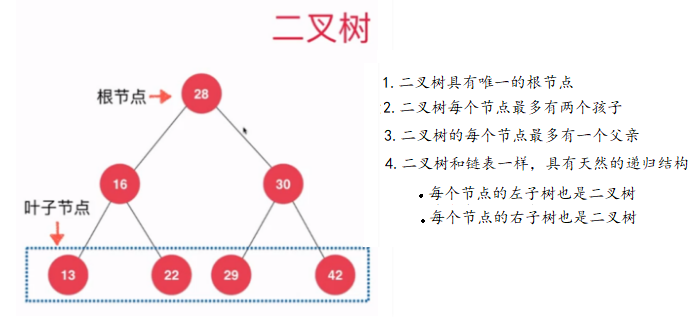 ###什麼是二分搜尋樹? 二分搜尋樹也是一種二叉樹,但二分搜尋樹種每個節點的值都要大於其左子樹所有節點的值,小於其右子樹所有節點的值,每一棵子樹也是二分搜尋樹。正因為二分搜尋樹的這種性質,二分搜尋樹儲存的元素必須具有可比較性。下圖就是一棵二分搜尋樹:  我們可以根據二分搜尋樹的特點,構建一顆二分搜尋樹,程式碼實現如下: ``` /** * 由於二分搜尋樹中的元素必須具有可比較性,所以二分搜尋樹中儲存的資料必須要實現Comparable介面 * @param
*/
public class BST> {
//由於使用者並不需要知道我們二分搜尋樹的具體實現,所以這裡把節點設定成內部類
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
//一棵樹只有一個根節點
private Node root;
//節點的個數
private int size;
//無參構造,這裡不寫也可以,因為和系統預設的無參構造是相同的
public BST(){
root = null;
size = 0;
}
//獲取節點的個數
public int size(){
return size;
}
//判斷樹是否為空
public boolean isEmpty(){
return size == 0;
}
}
```
### 二分搜尋樹的基本操作
#### 二分搜尋樹新增新元素
我們在向二分搜尋中新增元素時,需要保持二分搜尋樹的性質,即需要將我們新增的元素從根節點開始比較,若比根節點小,則去根節點的左子樹遞迴進行新增操作,若比根節點的右子樹遞迴進行新增操作,若相等,則直接返回,因為本文實現的是一棵不包含重複元素的二分搜尋樹。具體程式碼實現如下:
```
// 向二分搜尋樹中新增新的元素e
public void add(E e){
//判斷根節點是否為空
if(root == null){
//如果根節點為空,則將新新增的元素作為根節點
root = new Node(e);
//節點的個數加一
size ++;
}
else
add(root, e);
}
// 向以node為根的二分搜尋樹中插入元素e,遞迴演算法
private void add(Node node, E e){
//如果被新增的元素與當前節點的值相等,則直接返回 -- 本文的二分搜尋中不包含重複元素
if(e.equals(node.e))
return;
//如果待新增元素e小於當前節點的值,並且當前節點沒有左孩子
else if(e.compareTo(node.e) < 0 && node.left == null){
//則將待新增元素e作為當前節點的左孩子
node.left = new Node(e);
size ++;
return;
}
//如果待新增元素e大於當前節點的值,並且當前節點沒有右孩子
else if(e.compareTo(node.e) > bst = new BST();
int[] nums = {5, 3, 6, 8, 4, 2};
for(int num: nums){
//二分搜尋樹的新增操作
bst.add(num);
}
//前序遍歷 -- 遞迴演算法
bst.preOrder();
System.out.println();
System.out.println(bst);
}
```
我們現在根據上面的測試程式碼,來一起看下執行結果:

我們根據執行結果畫出的樹結構,可以看出是滿足二分搜尋樹的性質的,因此也證明了我們的新增方法和前序遍歷是沒有問題的。
2. 中序遍歷
根據我們的前序遍歷的遞迴實現,我們可以很容易地寫出二分搜尋樹的中序遍歷,具體實現如下:
```
//二分搜尋樹的中序遍歷 -- 遞迴演算法
public void inOrder(){
inOrder(root);
}
private void inOrder(Node node) {
if (node == null)
return;
//遍歷左子樹
inOrder(node.left);
//通過列印輸出該節點的值的形式,訪問該節點
System.out.print(node.e + "\t");
//遍歷右子樹
inOrder(node.right);
}
```
3. 後序遍歷
通過前序遍歷和中序遍歷的學習,我相信大家對後序遍歷的遞迴實現已經覺得非常容易了,程式碼如下:
```
//二分搜尋樹的後序遍歷 --遞迴演算法
public void postOrder(){
postOrder(root);
}
private void postOrder(Node node) {
if ( node== null )
return;
//遍歷左子樹
postOrder(node.left);
//遍歷右子樹
postOrder(node.right);
//通過列印輸出該節點的值的形式,訪問該節點
System.out.print(node.e+"\t");
}
```
* 非遞迴實現
***
1. 前序遍歷
實現思路:當我們使用非遞迴來實現二分搜尋樹的前序遍歷時,我們可以藉助棧這種資料結構,由於棧是後進先出的,我們需要先將當前節點的右孩子壓入棧中,再將當前節點的左孩子壓入棧中,當我們的棧不為空時,我們就迴圈執行出棧操作,並且將出棧的元素作為當前節點。當然,如果你還不瞭解棧這種資料結構,你可以看我的上篇文章:常見的線性結構進行學習。非遞迴前序遍歷具體程式碼實現如下:
```
//前序遍歷 -- 非遞迴實現
public List preOrderTraversal(TreeNode root) {
//該集合用來儲存通過前序遍歷後的元素
List res = new ArrayList();
if (root == null)
return res;
//藉助棧這種資料結構進行實現
Stack> stack = new Stack>();
//由於前序遍歷的一個元素一定是根節點,所以我們可以先將根節點壓入棧中
stack.push(root);
//判斷棧是否為空
while ( !stack.isEmpty() ){
//將出棧的節點儲存起來
TreeNode curr = stack.pop();
//將出棧節點的值新增到集合中
res.add(curr.val);
//若當前節點的右孩子不為空,就將該節點的右孩子壓入棧中
if (curr.right != null)
stack.push(curr.right);
//若當前節點的左孩子不為空,就將該節點的左孩子壓入棧中
if (curr.left != null)
stack.push(curr.left);
}
return res;
}
```
2. 中序遍歷
二分搜尋樹中序遍歷的非遞迴實現,這裡還是通過藉助棧來實現的,理解起來要比前序遍歷的非遞迴實現複雜一些,希望大家可以認真思考,仔細體會,具體程式碼實現如下:
```
//中序遍歷 -- 非遞迴實現
public List inOrderTraversal(TreeNode root){
List res = new ArrayList();
if (root == null)
return res;
TreeNode cur = root;
Stack stack = new Stack();
while (cur != null || !stack.isEmpty()){
if (cur != null) {
stack.push(cur);
cur = cur.left;
}else {
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
```
3. 後序遍歷
我們通過前面的前序遍歷和中序遍歷的非遞迴演算法的實現,都是採用的棧這種資料結構進行實現,這也和我們程式呼叫的系統棧的工作原理相似,下面我們後序遍歷的非遞迴演算法仍然接站棧這種資料結構進行實現,這樣可以幫助我們更加的熟悉棧這種資料結構的應用,具體程式碼實現如下:
```
//後序遍歷 -- 非遞迴演算法
public List postOrderTraversal(TreeNode root) {
List res = new ArrayList();
if (root == null)
return res;
//藉助棧結構實現二分搜尋樹的非遞迴後序遍歷
Stack stack = new Stack();
TreeNode curr = root;
TreeNode pre = null;
while (curr != null || !stack.isEmpty()) {
if (curr != null){
stack.push(curr);
curr = curr.left;
}else {
curr = stack.pop();
if (curr.right == null || curr.right == pre){
res.add(curr.val);
pre = curr;
curr = null;
}else {
stack.push(curr);
curr = curr.right;
}
}
}
return res;
}
```
4. 層序遍歷
層序遍歷和前面三種遍歷方式都不一樣,前、中、後序遍歷本質上都是深度優先遍歷,在進行前、中、後序遍歷時,會先一直走到二分搜尋樹的葉子節點,也就是最大深度,而我們的層序遍歷,本質上是一種廣度優先遍歷,就是橫向遍歷完所有節點後,再遍歷下一層節點,如下圖:
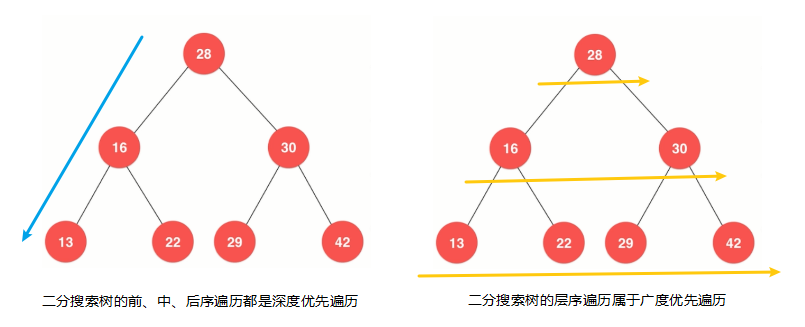
那麼二分搜尋樹的層序遍歷如何實現呢,我們前面講過佇列這種資料結構是先進先出的,我們可以將二分搜尋樹中的每層節點順序放進佇列中,然後再進行出隊操作就可以了,若你不清楚佇列,你可以看我的上篇文章常見的線性結構進行學習,現在就讓我們來看是如何使用佇列實現二分搜尋樹的層序遍歷吧,具體程式碼實現如下: ``` //層序遍歷 public void levelOrder(){ if (root == null) return; Queue queue = new LinkedList();
queue.add(root);
while ( !queue.isEmpty()){
Node removeNode = queue.remove();
System.out.print(removeNode.e+"\t");
if (removeNode.left != null)
queue.add(removeNode.left);
if (removeNode.right != null)
queue.add(removeNode.right);
}
}
```
#### 刪除二分搜尋樹中的元素
由於刪除二分搜尋中的任意元素是比較複雜的,我們可以先研究如何實現刪除二分搜尋樹的最大值和最小值,當然我們得先找到這棵二分搜尋樹的最大值和最小值,查詢方法如下:
```
//尋找二分搜尋樹中最大元素 -- 遞迴獲取
public E maxNum(){
if (size == 0)
throw new IllegalArgumentException("BST is empty");
//遞迴呼叫獲取二分搜尋中最大值所在的節點的方法
Node maxNode = maxNum(root);
return maxNode.e;
}
//以node為根節點,獲取二分搜尋中最大值所在的節點
private Node maxNum(Node node) {
//遞迴終止條件---如果當前節點的右孩子為空,則返回當前節點
if (node.right == null)
return node;
//遞迴從當前節點的右子樹獲取最大值所在的節點
return maxNum(node.right);
}
//尋找二分搜尋數中的最小元素 -- 遞迴法
public E minNum(){
if (size == 0) // 也可以寫為 root==null
throw new IllegalArgumentException("BST is empty");
Node minNode = minNum(root);
return minNode.e;
}
//以node為根節點搜尋最小元素所在的節點
private Node minNum(Node node) {
if (node.left == null)
return node;
//遞迴從當前節點的左子樹獲取最小值所在的節點
return minNum(node.left);
}
```
現在我們已經找出最小元素和最大元素所在的節點了,我們現在就可以是實現刪除最小元素和最大元素所在的節點操作了,程式碼如下:
```
//從二分搜尋樹中刪除最小元素所在的節點,並返回最小元素的值
public E removeMinNum(){
//獲取最小值
E e = minNum();
root = removeMinNum(root);
return e;
}
//以node為根節點刪除最小元素所在的節點
private Node removeMinNum(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMinNum(node.left);
return node;
}
//刪除二分搜尋數中最大元素所在的節點,並返回該值
public E removeMaxNum(){
//獲取最大值
E e = maxNum();
root = removeMaxNum(root);
return e;
}
//刪除以node為根節點的二分搜尋中最大元素所在的節點
private Node removeMaxNum(Node node) {
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMaxNum(node.right);
return node;
}
```
在我們實現刪除二分搜尋樹中的最大元素所在的節點和刪除最小元素所在的節點操作後,我們可以寫一個簡單的測試用例,來驗證下我們的刪除最大值和刪除最小值操作是否正確:
```
public static void main(String[] args) {
BST bst = new BST();
Random random = new Random();
int n = 1000;
// 測試刪除最小元素所在的節點
for(int i = 0 ; i < n ; i ++)
bst.add(random.nextInt(10000));
List nums = new ArrayList();
while(!bst.isEmpty()){
//從二分搜尋樹中刪除最小元素所在的節點,並拿到該最小元素
Integer minNum = bst.removeMinNum();
//向我們的集合中新增該最小元素
nums.add(minNum);
}
//我們的nums集合中儲存的是二分搜尋樹中所有節點的值按從小到大順序排序後的元素
System.out.println(nums);
for(int i = 1 ; i < nums.size() ; i ++)
//如果該集合中前一個元素的值大於後一個元素的值,則不滿足從小到大的排序規則,則丟擲錯異常
if(nums.get(i - 1) > ();
while(!bst.isEmpty()){
//從二分搜尋樹中刪除最大元素所在的節點,並拿到該最大元素
Integer maxNum = bst.removeMaxNum();
//向我們的集合中新增該最小元素
nums.add(maxNum);
}
//我們的nums集合中儲存的是二分搜尋樹中所有節點的值按從大到小倒序排序後的元素
System.out.println(nums);
for(int i = 1 ; i < nums.size() ; i ++)
//如果該集合中前一個元素的值小於後一個元素的值,則不滿足從大到小的排序規則,則丟擲錯異常
if(nums.get(i - 1) < nums.get(i))
throw new IllegalArgumentException("Error!");
System.out.println("removeMax test completed.");
}
```
有了如上操作作為鋪墊後,現在就可以來實現刪除二分搜尋樹中的指定元素的操作了,需要注意的是,當待刪除節點的左右子樹都不為空時,我們需要找到待刪除元素的後繼或者前驅,後繼就是指待刪除節點右子樹中最小的元素所在的節點,前驅是指待刪除節點左子樹最大的元素所在的節點。本文是採用的待刪除節點的後繼來代替待刪除元素的位置。
前驅圖示:待刪除節點右子樹中最小的元素所在的節點 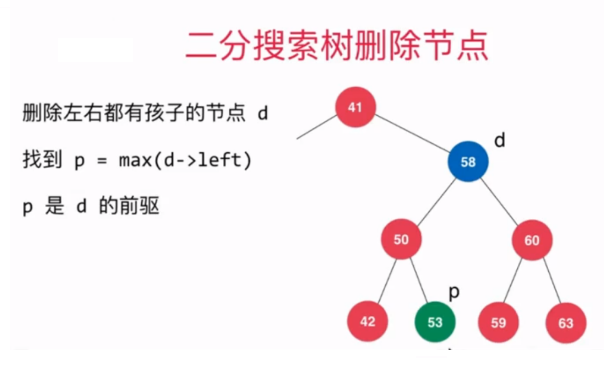 後繼圖示:待刪除節點左子樹最大的元素所在的節點 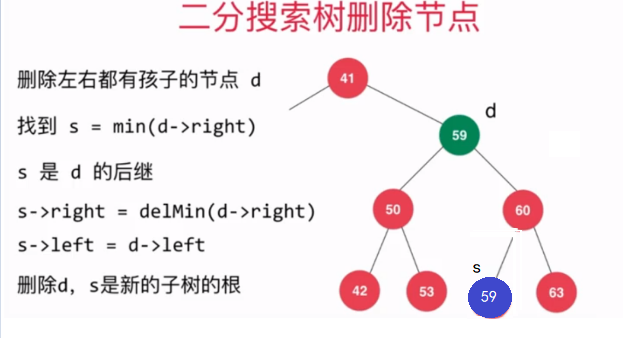
具體程式碼實現如下: ``` //刪除二分搜尋樹中的指定元素 public void removeElement(E e){ root = removeElement(root,e); } // 刪除掉以node為根的二分搜尋樹中值為e的節點, 遞迴演算法 // 返回刪除節點後新的二分搜尋樹的根 private Node removeElement(Node node, E e) { if (node == null) return null; if (e.compareTo(node.e) <0 ){ node.left = removeElement(node.left, e); return node; }else if (e.compareTo(node.e) >0 ){ node.right = removeElement(node.right,e); return node; }else { //e.compareTo(node.e) == 0 //待刪除節點左子樹為空的情況 if (node.left == null){ Node rightNode = node.right; node.right = null; size --; return rightNode; } //待刪除節點的右子樹為空的情況 if (node.right == null){ Node leftNode = node.left; node.left = null; size -- ; return leftNode; } //待刪除節點的左右子樹都不為空的情況 // 待刪除節點的後繼:找到比待刪除節點大的最小節點, 即待刪除節點右子樹的最小節點 // 用這個節點頂替待刪除節點的位置 Node successor = minNum(node.right); successor.right = removeMinNum(node.right); successor.left = node.left; node.right = node.left = null; return successor; } } ``` 本文實現的是一個不包含重複元素的二分搜尋樹,若你需要你的二分搜尋樹包含重複元素,在進行新增操作時只需要定義左子樹小於等於節點;或者右子樹大於等於節點。二分搜尋樹的學習就到這裡了,希望本文能讓你對二分搜尋樹有更深的理解。
樹和連結串列一樣,都屬於動態資料結構,由於二分搜尋樹是二叉樹的一種,我們先來說說什麼是二叉樹。二叉樹具有唯一的根節點,二叉樹每個節點最多有兩個孩子節點,二叉樹的每個節點最多有一個父親節點,二叉樹具有天然遞迴結構,每個節點的左子數也是一棵二叉樹,每個節點的右子樹也是一顆二叉樹。二叉樹如下圖:  ###什麼是二分搜尋樹? 二分搜尋樹也是一種二叉樹,但二分搜尋樹種每個節點的值都要大於其左子樹所有節點的值,小於其右子樹所有節點的值,每一棵子樹也是二分搜尋樹。正因為二分搜尋樹的這種性質,二分搜尋樹儲存的元素必須具有可比較性。下圖就是一棵二分搜尋樹:  我們可以根據二分搜尋樹的特點,構建一顆二分搜尋樹,程式碼實現如下: ``` /** * 由於二分搜尋樹中的元素必須具有可比較性,所以二分搜尋樹中儲存的資料必須要實現Comparable介面 * @param
那麼二分搜尋樹的層序遍歷如何實現呢,我們前面講過佇列這種資料結構是先進先出的,我們可以將二分搜尋樹中的每層節點順序放進佇列中,然後再進行出隊操作就可以了,若你不清楚佇列,你可以看我的上篇文章常見的線性結構進行學習,現在就讓我們來看是如何使用佇列實現二分搜尋樹的層序遍歷吧,具體程式碼實現如下: ``` //層序遍歷 public void levelOrder(){ if (root == null) return; Queue
前驅圖示:待刪除節點右子樹中最小的元素所在的節點  後繼圖示:待刪除節點左子樹最大的元素所在的節點 
具體程式碼實現如下: ``` //刪除二分搜尋樹中的指定元素 public void removeElement(E e){ root = removeElement(root,e); } // 刪除掉以node為根的二分搜尋樹中值為e的節點, 遞迴演算法 // 返回刪除節點後新的二分搜尋樹的根 private Node removeElement(Node node, E e) { if (node == null) return null; if (e.compareTo(node.e) <0 ){ node.left = removeElement(node.left, e); return node; }else if (e.compareTo(node.e) >0 ){ node.right = removeElement(node.right,e); return node; }else { //e.compareTo(node.e) == 0 //待刪除節點左子樹為空的情況 if (node.left == null){ Node rightNode = node.right; node.right = null; size --; return rightNode; } //待刪除節點的右子樹為空的情況 if (node.right == null){ Node leftNode = node.left; node.left = null; size -- ; return leftNode; } //待刪除節點的左右子樹都不為空的情況 // 待刪除節點的後繼:找到比待刪除節點大的最小節點, 即待刪除節點右子樹的最小節點 // 用這個節點頂替待刪除節點的位置 Node successor = minNum(node.right); successor.right = removeMinNum(node.right); successor.left = node.left; node.right = node.left = null; return successor; } } ``` 本文實現的是一個不包含重複元素的二分搜尋樹,若你需要你的二分搜尋樹包含重複元素,在進行新增操作時只需要定義左子樹小於等於節點;或者右子樹大於等於節點。二分搜尋樹的學習就到這裡了,希望本文能讓你對二分搜尋樹有更深的理解。
