程式設計師必學:快速冪演算法
前陣子,有小夥伴在我B站的演算法教程底下留言

小夥伴們有任何疑問或者希望我講解任何內容,都可以在我的個人B站或公眾號(xmg_mj)留言哦,我會盡我最大能力、儘量抽時間去寫文章\錄視訊來回應大家。
關於快速冪
其實快速冪相關的問題,是參加演算法競賽(NOI、ACM等)的小夥伴必須要掌握的一小塊基礎內容。當然,就算你不打算參加演算法競賽,個人覺得只要你是一名程式設計師,就必須要掌握快速冪演算法。
在《計算機程式設計藝術》一書中就有提到快速冪演算法,此書的英文名是The Art of Computer Programming,簡稱TAOCP。

TAOCP出自Donald Ervin Knuth前輩之手。Knuth前輩是在計算機領域成就頗豐的知名科學家,是著名的KMP演算法的發明人之一,在1974年獲得“計算機領域的諾貝爾獎”:圖靈獎(當年他才36歲)。目前TAOCP已經出版了第1、2、3、4A卷,按照計劃,還有第4B、5、6、7卷未出版。第一卷首發於1968年,Knuth前輩今年是82歲高壽,據說他計劃在105歲之前完成這部鉅著。

關於TAOCP,微軟創始人Bill Gates曾說過
If you think you're a really good programmer… read (Knuth's) Art of Computer Programming… You should definitely send me a resume if you can read the whole thing.
大概意思是:如果你認為自己是一位非常優秀的程式設計師,那就應該閱讀Knuth的TAOCP;如果你能讀懂全部內容,可以直接給我傳送一份簡歷。據說Knuth前輩的言辭更加犀利:看不懂就別當程式設計師了!不過TAOCP對於新手來說,閱讀難度的確比較大,書中的所有示例都使用了Knuth前輩自創的MIX組合語言。
閱讀本文之前的提醒
今天就抽空寫一篇文章來講解一下經典的快速冪演算法哈。不過要想徹底看懂本文,有幾個前提條件
- 熟悉演算法中的2個基礎概念:時間複雜度、空間複雜度
- 如果你壓根沒聽過這2個概念,說明你的演算法基礎完全為0,真的沒有在開玩笑!
- 可以向公眾號傳送複雜度獲取相關教程
- 熟悉二進位制和十進位制的轉換
- 如果連這個都不熟悉的話,那你的程式設計底子就真的需要好好補補啦
- 可以向公眾號傳送進位制獲取相關教程
- 熟悉常見的位運算操作
- n & 1的結果是n最低二進位制位的值,也可以用於判斷n的奇偶性
- 求正整數n / 2,可以用位運算取代:n >> 1
- 如果不明白上述操作的原理,可以向公眾號傳送位運算獲取相關教程
什麼是冪(Power)?
眾所周知,x的n次冪,是指x的n次方,也就是n個x相乘,比如2的4次冪就是2 * 2 * 2 * 2。
為了簡化描述,後面x的n次冪,我就簡化為x ^ n(本文中的 ^ 並不是按位異或的意思)
那如何通過程式設計求冪?假設只考慮x、n是整數且n大於等於0的情況,最容易想到的方法如下所示(這裡採用的程式語言是Java,但沒有涉及Java特殊的語法。所以就算你沒用過Java,也可以看懂)
int power(int x, int n) {
int result = 1;
while (n-- > 0) {
result *= x;
}
return result;
}
很顯然,這種方法的時間複雜度是O(n)、空間複雜度是O(1)
什麼是快速冪?
所謂快速冪,就是用效率更高(時間複雜度更低)的方法求冪,可以將時間複雜度優化至O(logn)。這裡介紹2種求解方法:遞迴、非遞迴
遞迴
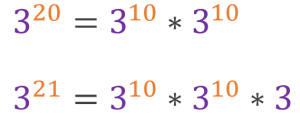
根據上圖中的等式,不難寫出以下程式碼
int fastPower(int x, int n) {
if (n == 0) return 1;
int result = fastPower(x, n >> 1);
result *= result;
return (n & 1) == 0 ? result : result * x;
}
這個方法的時間、空間複雜度都是O(logn)。
那如何分析出這個方法的複雜度呢?
如果你的演算法功底比較薄弱,可以代入特定值作一個大概的分析,比如當n為16時,方法的遞迴呼叫過程如下圖所示

不難看出,每次呼叫時,n的規模都減半,所以時間和空間複雜度都是O(logn)
如果你的演算法功底還行,那就可以用更專業的方法去分析它的複雜度(沒有一定的演算法基礎,可能會看不懂)
- 這其實是典型的應用分治策略的演算法
- 假設T(n)是資料規模為n時的時間複雜度,不難得出遞推式:T(n) = T(n / 2) + O(1)
- 最後根據遞推式 + 主定理(Master Theorem)可以直接得出結論:T(n) = O(logn)
非遞迴
我們以求3 ^ 21為例子,來分析一下非遞迴的程式碼應該怎麼寫。
首先21的二進位制形式是10101

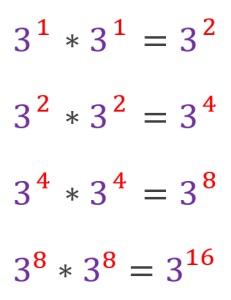
不難得出以下結論
- 3 ^ n(n為2、4、8、16)都可以由3 ^ 1累乘出來
- 每一個3 ^ n都有對應的二進位制位
- 3 ^ 1對應二進位制位的值是1,其實是二進位制10101的最後1位
- 3 ^ 2對應二進位制位的值是0,其實是二進位制1010的最後1位
- 3 ^ 4對應二進位制位的值是1,其實是二進位制101的最後1位
- 3 ^ 8對應二進位制位的值是0,其實是二進位制10的最後1位
- 3 ^ 16對應二進位制位的值是1,其實是二進位制1的最後1位
- 如果3 ^ n對應二進位制位的值是0,就不用乘進最終結果
- 比如3 ^ (8 * 0)、3 ^ (2 * 0)
- 因為它們最終的值都是3 ^ 0,也就是1
- 如果3 ^ n對應二進位制位的值是1,就需要乘進最終結果
- 比如3 ^ (16 * 1)、3 ^ (4 * 1)、3 ^ (1 * 1)
所以,綜合以上種種結論,可以總結出以下解題步驟
- 利用3 ^ 1,不斷累乘出3 ^ n(n為2、4、8、16)
- 每當累乘出一個3 ^ n,就檢視其對應二進位制位的值是1還是0,來決定是否要將它乘進最終結果
int fastPower(int x, int n) {
int result = 1;
while (n != 0) {
if ((n & 1) == 1) {
result *= x;
}
x *= x;
n >>= 1;
}
return result;
}
代入3和21,fastPower(3, 21)的執行流程如下
第1輪while迴圈
- 第4行程式碼
- n的二進位制是10101(十進位制是21)
- x = 3 ^ 1, 其對應二進位制位的值是1(n的最後一個二進位制位)
- 所以需要執行第5行程式碼:將x乘進最終結果
- result = 3 ^ 1
- 第7行程式碼
- x = (3 ^ 1) * (3 ^ 1) = 3 ^ 2
- 第8行程式碼
- n右移1位,其二進位制變成了1010(對應的十進位制是啥?不重要!!!)
第2輪while迴圈
- 第4行程式碼
- n的二進位制是1010
- x = 3 ^ 2, 其對應二進位制位的值是0(n的最後一個二進位制位)
- 所以不需要執行第5行程式碼:不需要將x乘進最終結果
- result = 3 ^ 1
- 第7行程式碼
- x = (3 ^ 2) * (3 ^ 2) = 3 ^ 4
- 第8行程式碼
- n右移1位,其二進位制變成了101(對應的十進位制是啥?不重要!!!)
第3輪while迴圈
- 第4行程式碼
- n的二進位制是101
- x = 3 ^ 4, 其對應二進位制位的值是1(n的最後一個二進位制位)
- 所以需要執行第5行程式碼:將x乘進最終結果
- result = (3 ^ 1) * (3 ^ 4)
- 第7行程式碼
- x = (3 ^ 4) * (3 ^ 4) = (3 ^ 8)
- 第8行程式碼
- n右移1位,其二進位制變成了10(對應的十進位制是啥?不重要!!!)
第4輪while迴圈
- 第4行程式碼
- n的二進位制是10
- x = 3 ^ 8, 其對應二進位制位的值是0(n的最後一個二進位制位)
- 所以不需要執行第5行程式碼:不需要將x乘進最終結果
- result = (3 ^ 1) * (3 ^ 4)
- 第7行程式碼
- x = (3 ^ 8) * (3 ^ 8) = 3 ^ 16
- 第8行程式碼
- n右移1位,其二進位制變成了1(對應的十進位制是啥?不重要!!!)
第5輪while迴圈
- 第4行程式碼
- n的二進位制是1
- x = 3 ^ 16, 其對應二進位制位的值是1(n的最後一個二進位制位)
- 所以需要執行第5行程式碼:將x乘進最終結果
- result = (3 ^ 1) * (3 ^ 4) * (3 ^ 16)
- 第7行程式碼
- x = (3 ^ 16) * (3 ^ 16) = 3 ^ 32
- 第8行程式碼
- n右移1位,其二進位制變成了0
最後
- 由於n = 0,所以退出while迴圈
- 最終result = (3 ^ 1) * (3 ^ 4) * (3 ^ 16)
- 複雜度分析
- 每執行一次while的迴圈體,n >>= 1, 會導致n的值減半
- 所以時間複雜度:O(logn)、空間複雜度:O(1)
Leetcode
Leetcode上的第50號題50. Pow(x, n),剛好就可以用今天講解的快速冪演算法。以下是我的程式碼實現
// 遞迴
public double myPow(double x, int n) {
if (n == 0) return 1;
if (n == -1) return 1 / x;
double half = myPow(x, n >> 1);
half *= half;
return ((n & 1) == 1) ? half * x : half;
}
// 非遞迴
public double myPow(double x, int n) {
long y = (n < 0) ? -((long) n) : n;
double result = 1.0;
while (y > 0) {
if ((y & 1) == 1) {
result *= x;
}
x *= x;
y >>= 1;
}
return (n < 0) ? (1 / result) : result;
}
需要提醒的是
- 這裡我用的程式語言是Java,大家可以根據自己熟悉的程式語言,對一些語法細節作出相應的調整
- Leetcode上的n可能是個負數,所以上面的程式碼針對負數的情況作了一些處理
更多快速冪相關的問題
時間有限,這篇文章就先說到這了哈。給小夥伴們留2個快速冪相關的問題,有空的話,可以去研究一下
- 使用矩陣快速冪求斐波那契數列
- 請設計一個演算法求x的y次冪模z的結果:(x ^ y) % z
- 假設x、y都可能是很大的整數(y大於等於0,z不等於0)
如果你特別希望我寫點什麼方面的內容,也可以留言建議,謝謝。歡迎關注

相關推薦
程式設計師必學:快速冪演算法
前陣子,有小夥伴在我B站的演算法教程底下留言 小夥伴們有任何疑問或者希望我講解任何內容,都可以在我的個人B站或公眾號(xmg_mj)留言哦,我會盡我最大能力、儘量抽時間去寫文章\錄視訊來回應大家。 關於快速冪 其實快速冪相關的問題,是參加演算法競賽(NOI、ACM等)的小夥伴必須要掌握的一小塊基礎內容。當
程式設計師必學的十個演算法
演算法一:快速排序演算法 快速排序是由東尼•霍爾所發展的一種排序演算法。在平均狀況下,排序 n 個專案要Ο(n log n)次比較。在最壞狀況下則需要Ο(n2)次比較,但這種狀況並不常見。事實上,快速排序通常明顯比其他Ο(n log n) 演算法更快,因為它的內部迴
程式設計師必學電腦計算機專業英語詞彙 01 (132 單詞)
file n. 檔案,公文箱,銼刀,[計算機] 檔案 vt. 列隊行進,歸檔,申請 command n.命令,指揮; 司令部,指揮部; [計算機]指令; 控制力 vt.指揮,控制,命令;
程式設計師必學電腦計算機專業英語詞彙 04 (200 單詞)
corner n.角落,角; 拐角; 困境; [商]囤積 vi.駕車轉彎; 聚於角落 vt.壟斷; 逼入困境 adj.位於角落的 present n. 禮物, 現在 adj. 當面的,
程式設計師必學電腦計算機專業英語詞彙 09 (111 單詞)
complexity n. 複雜,複雜性, 複雜的事物 creation n. 創造, 創作 unknown adj. 未知的,不出名的 greatly adv. 很
程式設計師必學電腦計算機專業英語詞彙 08 (118 單詞)
administrator n. 管理人,行政官 ensemble n. 全體, 合唱曲, 女人的全套服裝 bus n. 公共汽車 allowable adj. 容許
Laravel原始碼解析之入口,程式設計師必學
前言 提升能力的方法並非使用更多工具,而是解刨自己所使用的工具。今天我們從Laravel啟動的第一步開始講起。 入口檔案 laravel是單入口框架,所有請求必將經過index.php define(‘LARAVEL_START’, microtime(true
程式設計師面試題:快速找出一個數組中的兩個數字,讓這兩個數字之和等於一個給定的值
能否快速找出一個數組中的兩個數字,讓這兩個數字之和等於一個給定的值,為了簡化起見,我們假設這個陣列中肯定存在至少一組符合要求的解。 假如有如下的兩個陣列,如圖所示: 5,6,1,4,7,9,8 給定Sum= 10 1,5,6,7,8,9 給定Sum=
程式設計師必學電腦計算機專業英語詞彙 11 (125 單詞)
contiguous adj. 鄰近的,接觸的,連續的 consistent adj. 始終如一的, 一致的, 堅持的 multiprocessing n. 多重處理, 多處理
程式設計師必學電腦計算機專業英語詞彙 07 (142 單詞)
micro adj. 微小的 n. 微米(百萬分之一, 測微計) beyond adv. 在更遠處,另外 n. 遠處, 來世 prep. 超出, 越過,另外 against p
程式設計師必學,英文構詞字首
英語單詞的構詞規律也是有規可尋的。單詞是由詞素構成的,詞素派生出詞義。單詞的數量雖然浩瀚,但構成其的詞素的數量卻是有限的。如果掌握了詞素,懂得基本的構詞方法,就能容易地掌握英語單詞。 詞素又是由詞根和詞綴兩部分組成的,而詞綴又分為字首和字尾。常用的252個詞根
程式設計師必學電腦計算機專業英語詞彙 05 (200 單詞)
root n. 根,根源,祖先 vt. &vi. 生根,紮根,翻尋,起源於 symbol n. 符號, 標誌, 象徵 binary adj. 二進位的,二元的 n. 二
程式設計師必知的10大基礎實用性演算法
轉載自:http://www.apkbus.com/portal.php?mod=view&aid=9839 演算法一:快速排序演算法
在職程式設計師再學演算法的深刻感悟
一位已經在職程式設計師在再次學習演算法中,在方法上遇到了上點麻煩,他給我來信,併為他出了一些主意,見《一道演算法題引起的疑惑——如何“畫”演算法(附免費視訊連結)》。 隨後,他真的打通了這個環節。更難得的是,他在這一段時間內,已經進入到了一個新境界。從學習中的認知層次角度,他已經從上
如何快速鑑定菜鳥與大神程式設計師,網友:髮量是唯一標準!
剛剛走出就業的程式設計師,技術是剛剛起步的基點。現在社會上有很多程式設計師,“菜鳥”程式設計師和“大神”程式設計師差在哪裡?真是差在技術上了嗎? 有位網友在論壇上釋出了一個如何快速鑑別菜鳥和大神的程式設計師的貼紙,程式設計師們來看看說得對不對… 我們點開圖一個個的看。 從上
神級程式設計師帶來的:基於Python和Tensorflow的電影推薦演算法!
userIdmovieIdratingtimestamp9999967162682.5106557937010000067162694.0106514920110000167163654.0107094036310000267163852.510709796631000036
程式設計師必知(一):CSRF跨站請求偽造
首先說明一下什麼是CSRF(Cross Site Request Forgery)? 跨站請求偽造是指攻擊者可以在第三方站點製造HTTP請求並以使用者在目標站點的登入態傳送到目標站點,而目標站點未校驗
程式設計師吐槽:真心累,轉行花了數萬元學程式設計,卻連工作都找不到
網際網路紅利時代,激發了越來越多的人投身其中就業與創業,其中程式設計師這一職業也被推上了高薪職業風口。除了科班畢業的程式設計師,也有不少傳統行業從業者轉行進入網際網路行業,這些半路轉行的有的會通過自學,有的則會通過花錢上培訓班達到速成的效果。然而俗話說轉行窮三年不是沒有道理的,畢竟從事一個全新的崗位
睡眠十律:程式設計師必看
前幾天在微博上看到了一個叫“BBC之睡眠十律”的視訊。 視訊地址:http://v.youku.com/v_show/id_XMzgzNTQ5NDQw.html 豆瓣電影:http://movie.douban.com/subject/19976842/ 看過之後,我覺得有必要總結一下要點。身為計算機專
