演算法與資料結構(4):堆排序
阿新 • • 發佈:2020-05-03
堆排序(HeapSort)是最常用的排序演算法之一。這種排序演算法同時具有插入排序和歸併排序的優點。與插入排序一樣,具有**空間原址性**,即**任何時候都只需要常數個額外的空間儲存臨時資料**(對此,請大家回想一下歸併排序,隨著問題規模的越大,需要的額外空間就越大,在解決大型問題時,這是不可接受的缺點)。與歸併排序一樣,具有 $O(n*lgn)$ 的時間複雜度。
其實一句話總結,堆排序具有 $O(1)$ 的空間複雜度,具有 $O(n*lgn)$ 的時間複雜度。
同時,在這裡需要強調一點,此文所說的堆是一種**資料結構**,其類似於我們[上一篇文章](https://albertcode.info/?p=102)所說的**樹**,在一些高階語言中,例如 **Java** 中,“堆”是一種“**垃圾收集儲存機制**”,這僅僅是因為 Java 的 “垃圾收集儲存機制” 最早的資料結構採用的是“堆”。因為這個系列是介紹演算法與資料結構的,所以此係列後續提到的所有“堆”,都是隻一種資料結構,希望讀者在自行了解相關知識時,注意區分。
此文堆排序的完整程式碼可以在我的[github](https://github.com/AlbertShenC/Algorithm/tree/master/HeapSort)上檢視。
### 堆
如下圖所示,**(二叉)堆**可以被理解為一個**完全二叉樹**:
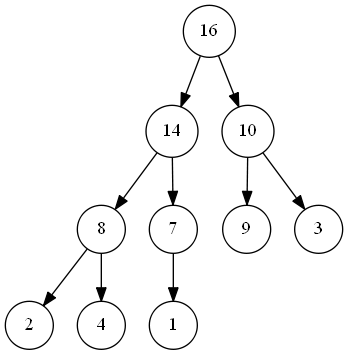
通常情況下,我們**採用陣列來儲存**(雖然我們也可以採用[上一篇文章](https://albertcode.info/?p=102)中提到的樹來實現,但這必然會帶來額外的複雜度。雖然我們採用陣列實現,但在理解時請將其視為樹,[檢視註釋](#註釋))。

除了最底層外,該樹是完全充滿的,而且最底層是從**左往右依次填充**。表示堆的陣列應該包括兩個屬性,heap_length 和 heap_size ,其中 heap_length 表示**陣列總長度**,heap_size 表示**有效資料個數**,同時滿足 $0 \leq heap\_size \leq length$ 。為了方便寫程式碼,我們如下定義:
```c
#define HEAP_LENGTH 20 // 陣列長度
int array_to_sort[HEAP_LENGTH + 1] = {HEAP_LENGTH, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
20, 19, 18, 17, 16, 15, 14, 13, 12, 11};
```
我們將 array_to_sort[0] 解釋為 heap_size,故 array_to_sort 的實際長度應為 heap_length + 1。這樣做的目的其實是為了下文方便,給定一個節點下標 i ,那麼他的父節點,左孩子和右孩子節點下標分別為:
```c
#define PARENT(i) (i / 2)
#define LEFT(i) (2 * i)
#define RIGHT(i) (2 * i + 1)
```
對於大多數的計算機而言,通過將 i 的值**算數左移**一位,即可在一條指令內計算出 2i,將 i 的值**算數右移**一位,即可在一條指令內計算出 $\lfloor \frac{i}{2} \rfloor$ ,不過在現代編譯器中,編譯器會自動將乘2與除2運算自動優化為移位操作,所以我們在寫程式碼時如果需要乘除法,儘量只進行乘2與除2操作即可。
二叉堆可以分為兩種形式:**最大堆**和**最小堆**。最小堆是指 除了根節點以外的其他所有節點 i 都需要滿足:
$$
A[PARENT(i)] \leq A[i]
$$
即某個節點的值**至多與其父節點一樣小**,因此堆中的最小元素存放在根節點中,並且此樹的任意子樹中,該子樹的中的所有元素的最小值也在子樹的根節點。最大堆與此正好相反,是指 除了根節點以外的所有節點 i 都有:
$$
A[PARENT(i)] \geq A[i]
$$
此文中採用的**堆排序**使用**最大堆**。
如果我們把堆看成一棵樹,則堆中**某個節點的高度**為該節點到葉節點的**最長簡單路徑**上的邊的數量,而**堆的高度**為根節點的高度。
下文的程式碼中,會涉及到swap函式,我們先將此函式的程式碼展示一下:
```c
// 交換陣列array的 下標i 和 下標j 對應的值
int swap(int *array, int i, int j){
int temp;
temp = array[i];
array[i] = array[j];
array[j] = temp;
return 0;
}
```
### 維護堆
首先展示一下程式碼:
```c
// 遞迴維護最大堆
int MaintainMaxHeap(int *heap, int i){
int largest;
int left = LEFT(i);
int right = RIGHT(i);
if(left <= heap[0] && heap[left] > heap[i]){
largest = left;
} else{
largest = i;
}
if(right <= heap[0] && heap[right] > heap[largest]){
largest = right;
}
if(largest != i){
swap(heap, largest, i);
MaintainMaxHeap(heap, largest);
}
return 0;
}
```
此函式的作用是維護最大堆的性質。函式的輸入為一個堆(陣列)heap,一個下標 i 。呼叫前,呼叫者需要保證**根節點為 LEAT(i) 和 RIGHT(i) 的二叉樹都是最大堆**(具體保證方法下文會闡述),此時我們需要將以下標 i 為根節點的子樹修改為最大堆(因為heap[i] 可能小於 heap[LEFT(i)] 或 heap[RIGHT(i)] )。
在程式碼中,我們從 heap[i] 和 heap[LEFT(i)] 、heap[RIGHT(i)] 中選出值最大的數,將其下標儲存在 largest 中。若heap[i] 就是最大值,說明此堆已經符合最大堆的特性,無需進行其他操作;反之則將 heap[i] 與 heap[largest] 交換,交換後,下標為largest的節點是原來的 heap[i],以此節點為根節點的子樹有可能也會違反最大堆的特性,那麼我們此時只需再對此節點呼叫一次 MaintainMaxHeap() 函式,如此遞迴下去,完成堆的維護。
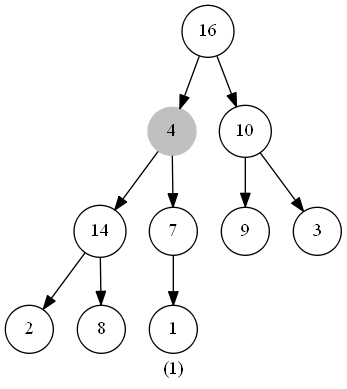
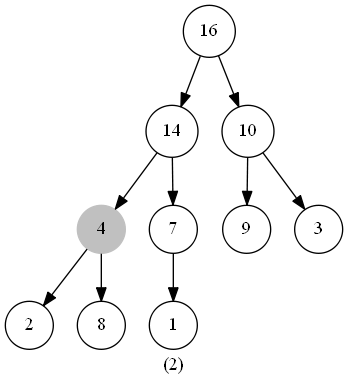
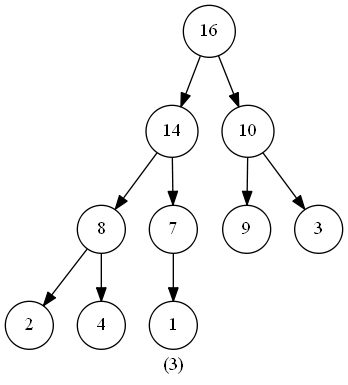
#### 時間複雜度
對於一棵以 i 為根節點,大小為 n 的子樹,MaintainMaxHeap() 的時間消耗分為兩部分:**調整** heap[i],heap[LEFT(i)],heap[RIGHT(i)] ,代價為 $\Theta(1)$ ;若進行了交換,**維護** i 節點的一個子樹的時間(時間複雜度一般指最壞情況,所以我們需要假定遞迴呼叫會發生)。而每一個孩子的子樹大小至多為 $\frac{2n}{3}$ (取最壞情況,樹的底層正好半滿,即左子樹的深度正好比右子樹大1,且左子樹是一個完全二叉樹),那麼,執行一次 MaintainMaxHeap() 的時間消耗為:
$$
T(n) \leq T(\frac{2n}{3}) + \Theta(1)
$$
由主定理可得,上述遞迴式的解為 $T(n)=O(lgn)$ 。
### 建堆
上文我們提到,在維護堆的性質時,需要保證左右子樹均為最大堆,那麼最為簡單的方法就是讓整個堆都變成最大堆,這樣,如果替換了一個數,他的左右子樹必能保證為一個最大堆。
對此,我們採用**自底向上**的方法,把一個大小為 n 的陣列轉換為最大堆。
```c
// 建堆
int BuildHeap(int *heap){
int i;
for(i = PARENT(heap[0]); i >= 1; i--){
MaintainMaxHeap(heap, i);
}
return 0;
}
```
#### 正確性分析
**初始化**:在第一次迴圈以前,$i=\lfloor \frac{n}{2} \rfloor$ ,而 $\lfloor \frac{n + 1}{2} \rfloor$ , $\lfloor \frac{n + 2}{2} \rfloor$ ,... ,$n$ 都是葉節點,故**下標大於 i 的節點都是一個最大堆的根節點**。
**保持**:因為節點 i 的孩子節點下標均大於 i ,故以節點 i 的子節點為根節點的樹都是一個最大堆,所以我們可以對節點 i 呼叫 MaintainMaxHeap() 函式,呼叫完成後,以節點 i 為根節點的樹是一個最大堆,其他下標大於 i 的節點要麼不受影響,要麼在 MaintainMaxHeap() 函式中,依然保持了最大堆的性質。一次迴圈結束,i 自減,**此時下標大於 i 的節點都是一個最大堆的根節點**。
**終止**:迴圈結束時,i==0,那麼此時**下標大於 0 的節點都是一個最大堆的根節點**,即整個樹已經成為了一個最大堆(heap[0]中儲存的是 heap_size,不是堆中的元素,希望各位讀者不要忘記了)。
#### 時間複雜度
對於這個過程,我們可以進行簡單的估算。每次呼叫 MaintainMaxHeap() 函式,其時間複雜度不超過 $O(lgn)$ ,MaintainMaxHeap() 函式一共被呼叫 $O(n)$ 次,那麼其時間複雜度不超過 $O(n*lgn)$ 。這個上界雖然正確,但不夠精確。我們下面來進行一下進一步的分析(如果讀者的數學水平有限的話,可以暫時跳過下面的具體分析)。
首先,對於一個含 $n$ 個元素的堆,其高度為 $\lfloor lgn \rfloor$ ,其中高度為 $h$ 的節點,最多有 $\lceil \frac{n}{2^{h+1}} \rceil$ 個(請各位讀者再仔細看一下上文的關於**堆的高度的概念**,之前教朋友的時候,很多人是把概念都弄錯了,從而覺得是我這個地方算錯了2333)
在一個高度為 $h$ 的節點上執行 MaintainMaxHeap() 的時間複雜度是 $O(h)$ ,那麼 BuildHeap() 的總的時間複雜度為
$$
\sum_{h=0}^{\lfloor lgn \rfloor} {\lceil \frac{n}{2^{h+1}} \rceil}O(h) = O(n \sum_{h=0}^{\lfloor lgn \rfloor} {\frac{h}{2^h}} )
$$
使用無窮級數或者數列的知識,我們可以得到:
$$
\sum_{h=0}^{ \infty } {\frac{h}{2^h}} = \frac{1/2}{(1-1/2)^2} = 2
$$
那麼最終的時間複雜度為:
$$
O(n \sum_{h=0}^{\lfloor lgn \rfloor} {\frac{h}{2^h}} ) = O(n \sum_{h=0}^{ \infty } {\frac{h}{2^h}}) = O(2n) = O(n)
$$
沒想到吧,我們居然可以在**線性時間**內,把一個無序陣列**構造**為一個**最大堆**。
### 堆排序
前面鋪墊了這麼多,終於進入正題了,如何進行堆排序?
```c
// 堆排序
int HeapSort(int *heap){
int i;
BuildHeap(heap);
for(i = heap[0]; i >= 1; i--){
swap(heap, 1, heap[0]);
heap[0] -= 1;
MaintainMaxHeap(heap, 1);
}
}
```
步驟非常簡單,首先**建立一個最大堆**,那麼此時陣列中的**最大元素**就在根節點 heap[1] ,此時我們將其與 heap[heap_size] 交換,我們即可將此元素**放在正確的位置**(最終的排序效果為遞增),此時我們將 heap_size 減一,將剛才被選出的最大值從堆中**去掉**。對於此時的堆,根節點的兩個子樹依然保持著最大堆的特性,但根節點可能會違背最大堆的特性,此時我們呼叫 MaintainMaxHeap(heap, 1) 即可將其**重新轉換為一個最大堆**,重複此操作,直到將所有節點均從堆中去掉,那麼整個陣列也就排序完成了。
#### 時間複雜度
堆排序的第一步是建立一個最大堆,其時間複雜度我們已經在上文分析了,為 $O(n)$ 。
呼叫 n 次 MaintainMaxHeap(),每次的時間複雜度為 $O(lgn)$ 。
那麼總的時間複雜度為 $O(n*lgn)$ 。
不過此時可能就會有好奇的讀者問了,在建堆的過程中,需要呼叫 $n$ 次,每次複雜度不超過 $O(lgn)$ ,這不是和堆排序是一樣的嗎?為什麼建堆最後算出來時間複雜度是 $O(n)$ ,而堆排序就是 $O(n*lgn)$ 呢?是的,關於堆排序的時間複雜度的計算我只是給了一個感性的估計方法,如果想要非常精確的計算出來的話,也是需要像建堆時那樣一步一步計算的,只是計算出來的結果也依然是 $O(n*lgn)$ ,所以為了偷懶,我就不驗算了嘛,畢竟還是挺費時的。
### 註釋
前文我們提到[對於堆這種資料結構,雖然我們採用陣列實現,但在理解時請將其視為樹](#堆),其實在計算機中,所有的內容都是 0-1 串,無論你是儲存了一張圖片,還是一個word文件,他們都是 0-1 串,但為什麼會有不同的呈現方式呢?其實就是對其的**解釋不同**。例如在 Windows 作業系統下,檔案具有一個屬性叫做字尾名,當你修改了其後綴名以後,檔案內容其實什麼都沒有變化,唯一的變化是對其解釋不同了。例如對於一個 html 檔案,當你把他解釋為一個網頁時,可以使用瀏覽器開啟,效果就是我們平時所看到的各種網頁,當你把他解釋為一個文字檔案時,就可以使用記事本或者其他編輯器開啟,你就能檢視他的原始碼。Windows 採用字尾名的方式,一是為了方便**自動選擇**合適的軟體開啟某個檔案(當然,你是可以在每次開啟時手動選擇的,但每次都手動選擇,是真的不適合我這種懶人),二是**方便使用者瞭解檔案內容**,比如當用戶看到一個字尾名為 png 的檔案時,就能知道這大概率是圖片(畢竟不能排除有人故意亂改字尾名),字尾名是 zip 時,能知道這是一個壓縮包。而在 Linux 下,系統選擇開啟某個檔案的軟體時,只檢視檔案開頭的一部分字串(不同的檔案格式具有不同的檔案頭,或者被稱為魔數),據此來判斷檔案格式,而後綴名的作用就只有我們上文所說的第二個作用了。
### 結語
本文我們詳細介紹了堆排序的相關內容,如果前面幾篇文章認真看了的話,理解起來也並不困難,如果只是想要知道堆排序怎麼寫的話,似乎前面幾篇文章頁不需要看2333,畢竟主要難度還是在於**時間複雜度的計算**上。但如果想要深入理解演算法這個巨坑的話,建議打好**數學基礎**,在時間複雜度的計算上,數學基礎是很重要的。下一篇文章我們將會介紹快速排序。
原文連結:[albertcode.info](https://albertcode.info/?p=129)
個人部落格:[albertcode.info](https://albertco
