有一本小冊子Static Single Assignment Book寫的很好，內容又較少，試著翻譯一下，意譯較多（說人話），不是嚴肅的翻譯，感興趣的可以看看。頻率可能是周更。。anyway，stay tuned～ 在日常程式設計中，名字是一個很有用的東西。這本書想傳遞的關鍵內容是對於每個不同的東西給它一個獨一無二的名字可以消除很多不確定性以及不精確性。 舉個例子，如果你無意中聽到一段對話中有'Homer'這個詞，沒有上下文的情況下你不知道他說的是Homer Simpson（辛普森）還是古希臘詩人荷馬還是你認識的某個叫Homer的人。但是隻要你聽到對話提及Springfield (辛普森一家）而不是Smyrna（希臘詩歌），你就能知道他們說的是辛普森一家這個電視劇。不過話又說回來，如果每個人都有一個獨一無二的名字，那麼就不可能混淆電視劇角色和古希臘文學人物，這個問題都不會成立。 這本書主要討論靜態單賦值（Static Single Assignment Form，SSA）形式，它是一種變數的命名約定。術語static說明SSA與屬性和程式碼分析相關，術語single說明SSA強制變數名具有唯一性。術語assignment表示變數的定義。舉個例子，在下面的程式碼中： ``` x = y + 1; ``` 變數x被賦予表示式(y+1)的值。這是一個定義，或者對於x來說是賦值語句。編譯器工程師會說上面的賦值語句將值(y+1)儲存到左值x中。 ## 1.1 SSA定義 關於SSA最簡單，限制最少的定義如下： > "如果每個變數在程式中有且只有一個賦值語句，那麼該程式是SSA形式" 但是實際上SSA還有很多變體，有更多的限制。這些變體可能使變數定義和使用與圖論的一些特性有關，或者封裝一些特定的控制流/資料流資訊。每個SSA變體都有特設的性質。基本的SSA變體將會在第二章討論，本書的第三部分還會討論更多這部分的內容。 所有SSA變體，包括上面最簡單的定義都有一個最基本屬性就是引用透明性（referential transparency），所謂引用透明性是指程式中的每個變數只有一個定義，變數的值和它所在程式的位置無關。我們可能根據分支的條件完善對於某個變數的認識。舉個例子，不用看程式碼我們就知道下面if語句後緊跟著的then/else條件塊中x的值 ``` if (x == 0) ``` 因為x的值在這個if語句中是沒有改變的。函數語言程式設計語言寫的程式是引用透明的，引用透明性對於形式化方法和數學推理很有用，因為表示式的值只依賴它的子表示式而不依賴求值的順序或者表示式的副作用，或者其它表示式。對於一個引用透明的程式，考慮下面的程式碼片段： ``` x = 1; y = x + 1; x = 2; z = x + 1; ``` 一個naive（而且不正確）的分析器可能認為y和z的值相等，因為他們的定義是一樣的，都是(x+1)，然而x的值取決於當前程式碼位置是在第二個賦值的前面還是後面，即變數的值取決於上下文。當編譯器將這個程式碼段轉換為SSA形式時，它會具有引用透明性。轉換的過程會為一個變數的多次定義使用不同的名字（譯註：x1和x2）。使用SSA形式後，只有當x1和x2相等時y和z才相等。 ``` x1 = 1; y = x1 + 1; x2 = 2; z = x2 + 1; ``` ## 1.2 SSA的非形式化語義 在前一節中，我們看到了如何通過簡單的重新命名將程式碼轉換為SSA形式。賦值語句左邊被定義的變數叫做target，在SSA中，每個target都有唯一的名字。反過來，賦值語句右邊可以多次使用target，在這裡它們叫做source。貫穿本書，SSA的target名字定義都是變數名再加一個下標這種形式。一般來說這是不重要的實現細節，雖然它對於編譯器debug來說很有用。 φ函式是SSA最重要的一個概念，它很特別，又叫做偽賦值函式（pseudo-assignment function）。有些人也叫它notational fiction。ɸ函式的用途是合併來自不同路徑的值，一般出現在控制流的合併點。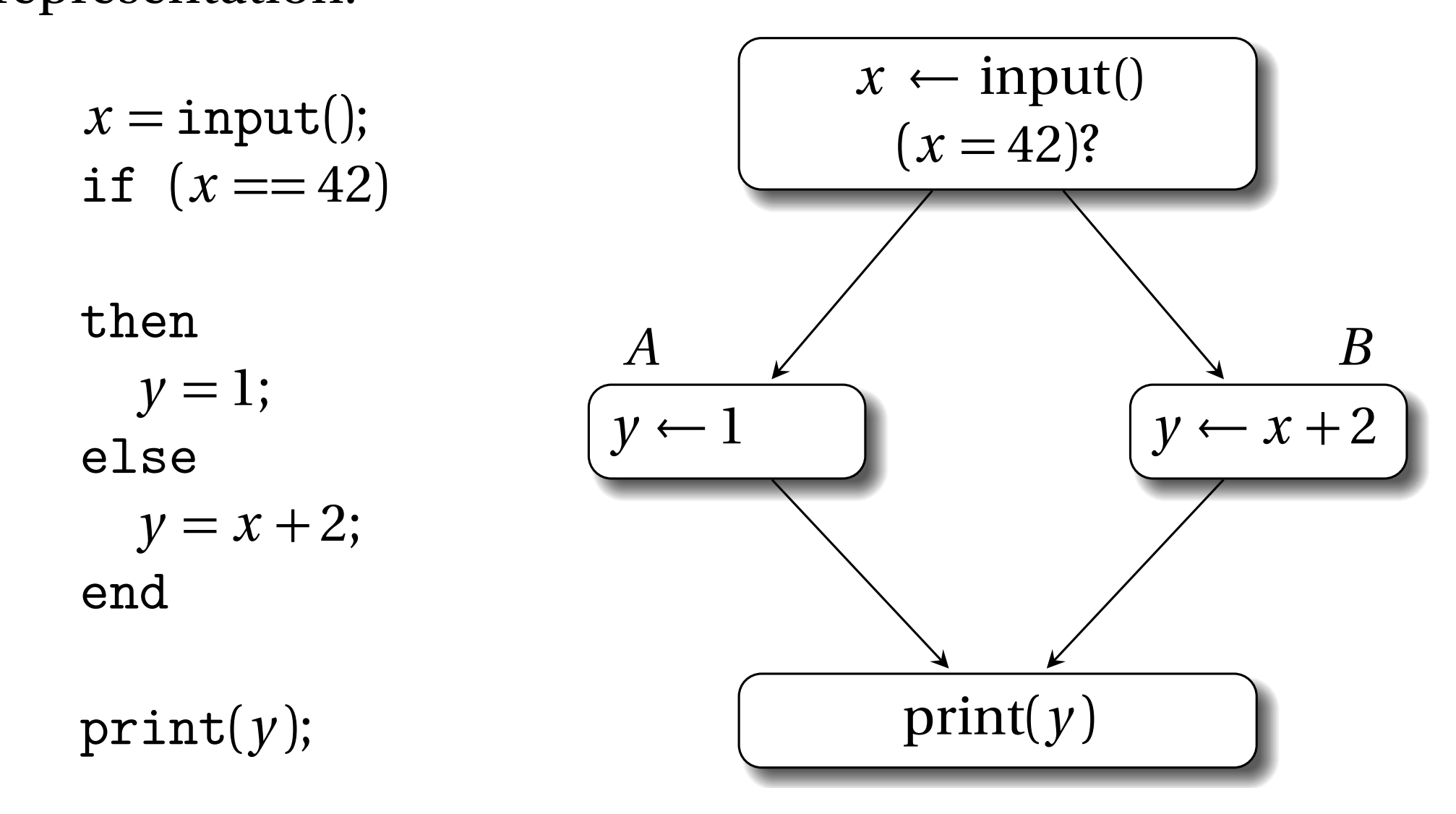 考慮下面的程式碼示例和它對應的控制流圖（Control Flow Graph，CFG）表示：  在if不同分支中，y有不同的定義。y的不同定義最終在print那個地方交匯。當編譯器將該程式碼轉換為SSA形式時，y的不同定義被命名為y1和y2。print既可以使用y1也可以使用y2，這取決於if的條件。在這種情況下，需要用φ函式引入新的變數y3，它的引數是y1和y2。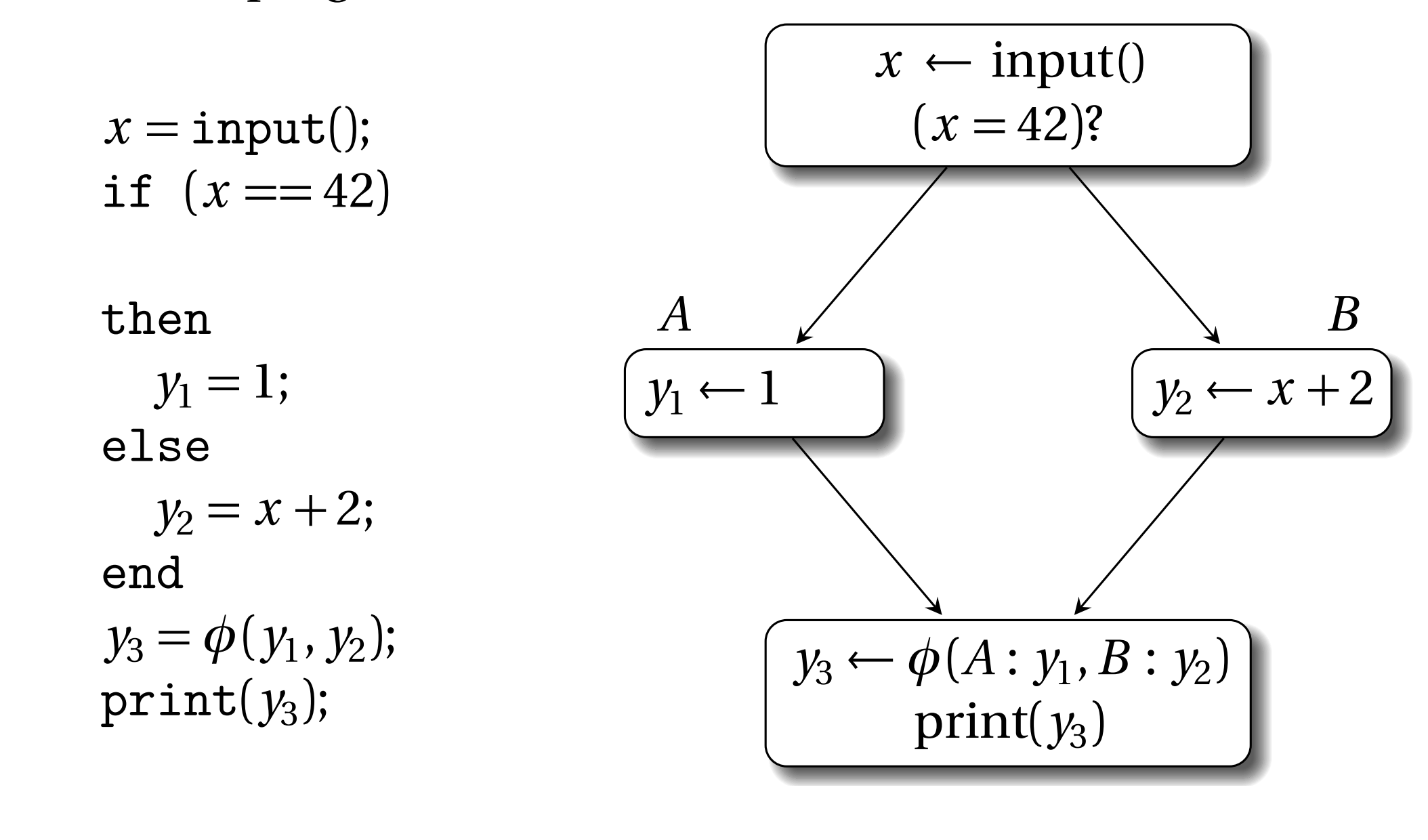因此SSA版本的上述程式如下：  就放置位置來說，φ函式一般是放到控制流交匯點，即CFG中有多個前驅基本塊的那個基本塊頭部。如果有n條路徑可以進入基本塊b，那麼在基本塊b頭部的φ函式有n個引數。φ函式會動態的選擇正確的引數。φ函式根據n個引數，建立新的變數名，這個名字是唯一的，因為它要保證SSA的基本性質。因此，在上面的例子中，如果控制流從基本塊A流向下面的基本塊，那麼y3使用φ函式選擇y1作為它的值，反之φ函式使用y2作為它的值。注意CFG圖φ函式的引數y1和y2前面還加了基本塊的標籤，這種形式是比較多餘的，在本書的後面部分，這個基本塊標籤能不加就不加，除非沒了它會引起歧義。 這裡還要強調一下，如果基本塊頭部有多個φ函式，這些φ函式是並行的，即，它們是同時執行，不需要順序執行。這一點是很重要的，因為在經過一些優化，比如複寫傳播（copy propagation）後φ函式的target可能是其它φ函式的source。在SSA解構階段，φ函式會被消除（譯註：就是編譯器不需要SSA形式，想將它轉換為其它IR，這就叫SSA解構），在解構階段使用常規的複製操作序列化，這點會在17.6小結描述。這個小細節對於暫存器分配後的程式碼來說是相當重要的。 嚴格來說，φ函式不能被軟體直接執行，因為進入φ函式的控制流沒有被顯式的編碼進φ函式的引數。這是可以接受的，因為φ函式通常只用於程式的靜態分析。然而，有很多擴充套件使得φ函式可以執行，如 φif 或者γ函式（參見第12章），它有一個額外的引數，告訴φ函式選擇那個值。關於這個會在第12章，第16章和第18章討論。 接下來我們再展示一個例子，它說明了一個迴圈控制流解構的SSA形式。下面是非SSA形式的程式和SSA形式的控制流圖：  SSA程式碼在迴圈頭部新增了兩個φ函式。它們合併迴圈前的值定義和迴圈中的值的定義。 要注意不要混淆SSA和自動並行化優化中的（動態）靜態賦值這兩個概念。SSA不會阻止在程式執行的時候對一個變數的多次定義，比如，上面的SSA程式碼中，變數y3和x3在迴圈體內，每次迴圈都會重定義它們。 SSA構造的詳細描述會在第3章給出，現在只需要明白下面的內容： 1. 如果程式的交匯點的某個變數有多個定義，那麼會在交匯點插入φ函式 2. 整數下標用於重新命名原來程式中的變數x和y ## 1.3 與傳統資料流分析的比較 在未來的第11章我們會提到，SSA主要的一個優點是它對資料流分析（data-flow analysis）很友好。資料流分析在程式編譯的時候收集資訊，為未來的程式碼優化做準備。在程式執行時，這些資訊會在變數間流動。靜態分析通過在控制流圖中傳播這些資訊，得以捕獲關於資料流的一些事實（fact）。這種方式在傳統的資料流分析中很常見。 通常，如果程式是一種功能性的（functional）或者稀疏（sparse）的表示，如SSA形式，那麼資料流資訊能程式中更高效的傳播。當程式被轉換為SSA形式時，變數在定義點被重新命名。對於一個確鑿的資料流問題，比如常量傳播，它表現為一個程式點的集合，在這些程式點資料流事實可能改變。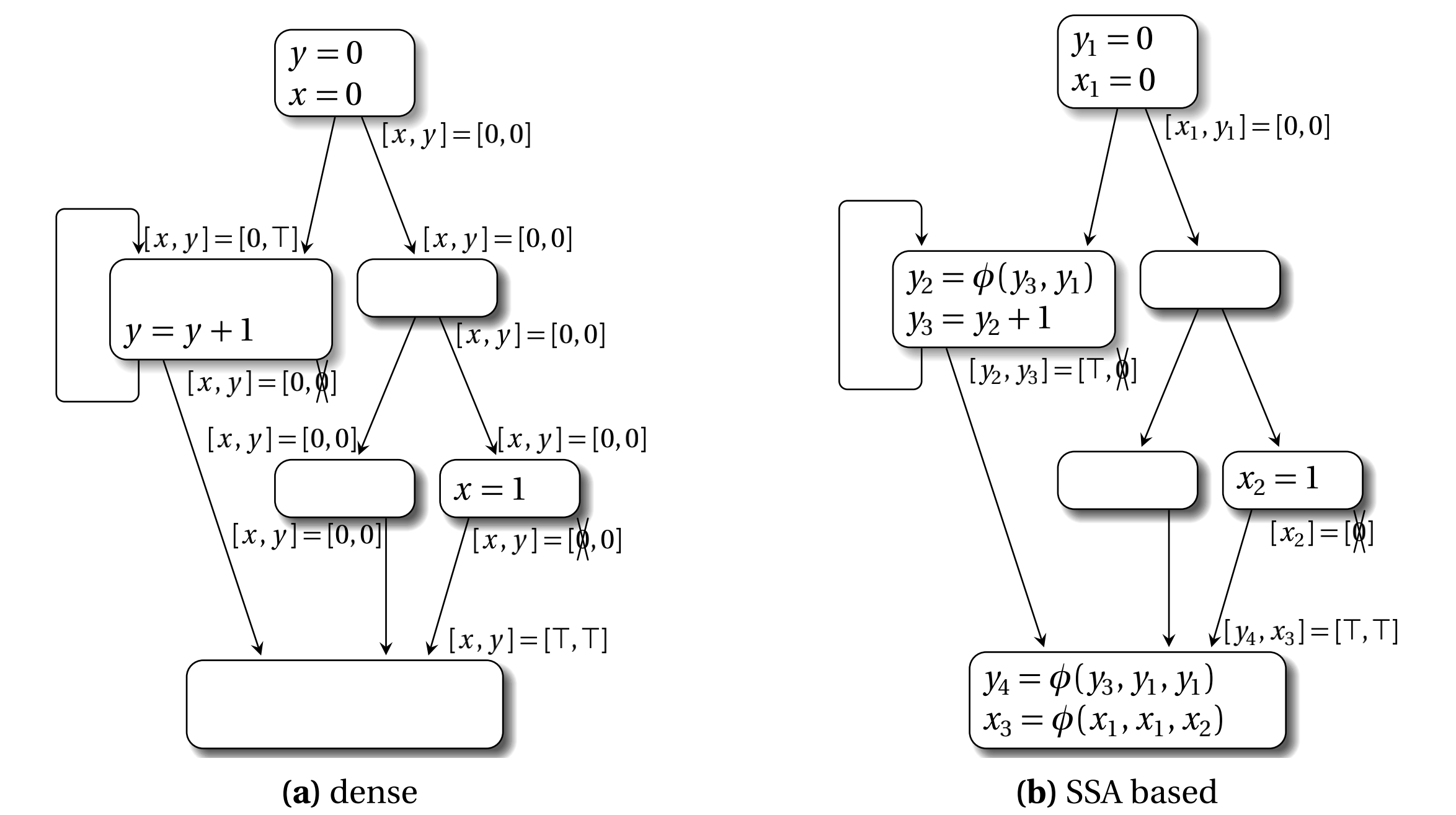因此可以直接關聯資料流事實和變數名字，而不是在每個程式點為所有變數維護各自的資料流事實的集合，下圖展示了一個非零值分析（non-zero value analysis）  對於程式中的每個變數，分析的目標是靜態確定哪些變數在執行時包含0值（即null）。在這裡0就表示變數為null，0打一把叉表示不為null，T表示可能為null。上圖(a)表示傳統的資料流分析，我們會在六個基本塊的入口點和出處都計算一次變數x和y資訊。而在上圖(b)的基於SSA的資料流分析中，我們只需要在變數定義處計算一下，然後就能獲得六個資料流事實。 對於其它的資料流問題，屬性也可能在變數定義之外發生改變，這些問題只要插入一些φ函式就能放入稀疏資料流分析的框架中，第11章會有一個例子討論這個。總的來說，目前這個例子說明了SSA能給分析演算法帶來的關鍵好處是： 1. 資料流資訊直接從定義語句處傳播到使用它的地方，即通過def-use鏈，這個鏈條由SSA命名方式隱示給出。相反，傳統的資料流分析需要將資訊傳遍整個程式，即便在很多地方這些資訊都沒改變，或者不相關。 2. 基於SSA的資料流分析更簡潔。在示例中，比起傳統方式，基於SSA的分析只有很少的資料流事實。 這本書的第二部分給出了一個完整的基於SSA資料流分析的描述。 ## 1.4 此情此景此SSA **歷史背景**。在整個20世紀80年代，優化編譯器技術越來越成熟，各種中間表示被提出，它們包含了資料依賴，使得資料流分析在這些中間表示上很容易進行。在這些中間表示背後的設計理念是顯式/隱式包含變數定義和使用的關係，即def-use鏈條，使得資料流資訊能有效的傳播。程式依賴圖（program dependence graph）和程式依賴網（program dependence web）均屬此類IR。第12章還會討論這些風格的IR的更多細節。 靜態單賦值是由IBM Research開發的一種IR，並在20世紀80年代末的幾篇研究論文中公開發表。SSA由於其符合直覺的性質和直觀的構造演算法得到了廣泛的應用。SSA給出了一個標準化的變數def-use鏈，簡化了很多資料流分析技術。 **當前狀況**。當前主流的商業編譯器和開源編譯器，包括GCC，LLVM，HotSpot Java虛擬機器，V8 JavaScript引擎都將SSA作為程式分析中的關鍵表示。由於在SSA執行優化速度快而且高效，那些即時編譯器（JIT）會在一些高階地、與平臺無關的表示（如Java位元組碼，CLI位元組碼，LLVM bitcode）上廣泛使用SSA。 SSA最初是為了簡化高階程式表示的變形而開發而建立的，因為其良好的特性，能夠簡化演算法和減少計算複雜性。今天，SSA形式甚至被用於最後的程式碼生成階段（見第四部分），即後端。好幾個工業編譯器和學術編譯器，既有靜態，也有just-in-time，都在它們的後端使用SSA，如LLVM，HotSpot，LAO，libFirm，Mono。很多使用SSA的編譯器在編譯快要結束時，即暫存器分配前才解構SSA。最近的研究甚至能在暫存器分配期間也使用SSA，SSA形式會保持到非常非常後面的機器程式碼生成過程才會被解構。 **SSA與高階語言**。到目前為止，我們展示了在低階程式碼上使用SSA形式做分析的優勢。有趣的是，在高階程式碼上如果強制遵循某些準則也可能具有SSA的性質。根據SISAL語言的定義，程式自動具備引用透明性，因為變數不允許多次賦值。其它語言也能有SSA的性質，比如Java的變數加個final或者C#的變數加個const/readonly。 強制寫出具有SSA性質的高階語言程式主要好處是這些程式能具備不變形，這簡化了併發程式設計。豬肚的資料能在多個執行緒中自由的共享，沒有任何資料依賴問題。資料依賴對於多核處理器來說是一個大問題。 在函數語言程式設計語言中，引用透明是語言的基本特性。因此函數語言程式設計隱式具有SSA性質。第6章會介紹SSA和函數語言程式設計。 ## 1.5 餘下本章 本章引入了SSA的符號表示，本書的剩下部分就SSA的各個方面詳細討論。本書的終極目標是： 1. 清晰的描述SSA能為程式分析帶來哪些好處 2. 消除那些阻止人們使用SSA的謬誤 本節還剩下一些內容，它們與下一章的一些主題相關。 ### 1.5.1 SSA的好處 SSA對於變數命名有嚴格要求，每個變數的名字都是獨一無二的。賦值語言和控制流交匯點會引入新的變數名。這些簡化了表達變數def-use關係的資料結構實現和變數存活範圍。本書第二部分關注基於SSA的資料流恩熙，使用SSA主要有三個好處： **編譯時受益**。如果程式是SSA形式，很多編譯器優化可以高效的進行，因為引用透明性意味著資料流資訊直接與變數關聯，而不是每個程式點的變數。關於這一點我們已經在1.3的非零值分析中演示過了。 **編譯器開發受益**。SSA使得程式分析和轉換能更容易表達。這意味著編譯器工程師能更高產，可以寫更多的pass，並且能debug更多的pass（譯註：smile）。舉個例子，基於SSA的GCC4.x的死程式碼優化比非GCC3.x的非SSA死程式碼優化實現總程式碼少了40%。 **程式執行時受益**。理論上，能基於SSA實現的分析和優化也能基於其它非SSA形式。前一點提到過，基於SSA的實現程式碼更少，因此很多基於SSA的編譯器優化也能更高效進行，關於這一點的示例是一類控制流不敏感分析（control-flow insensitive analysis），具體參見論文[Using static single assignment form to improve flowinsensitive pointer analysis]() ### 1.5.2 SSA謬論 一些人認為SSA很複雜很繁瑣，不能高效表達程式。這本書的目的就是讓讀者免去這些擔憂。下面的表單展示了關於SSA常見的謬論，以及破除謬論的章節。 | 謬論 | 破除謬論 | | ---- | ---- | | SSA讓變數數爆炸 | 第二章會回顧SSA的主要變體，一些變體引入的變數數比原始SSA形式少很多 | | SSA的性質難以維持 | 第三章和第五章討論了一些修復SSA性質的簡單技術（因為一些優化可能重寫中間表示，導致SSA性質被破壞）| | SSA的性質難以維持 | 第三章和第十七章展示了高效且效果顯著的SSA解構演算法的複製