解惑3:時間頻度,演算法時間複雜度
阿新 • • 發佈:2020-06-27
## 一、概述
先放百科上的說法:
> 演算法的**時間複雜度**(Time complexity)是一個函式,它定性描述該演算法的執行時間。這是一個代表演算法輸入值的字串的長度的函式。
>
> 時間複雜度常用大O符號表述,不包括這個函式的低階項和首項係數。使用這種方式時,時間複雜度可被稱為是漸近的,亦即考察輸入值大小趨近無窮時的情況。
>
> 例如,如果一個演算法對於任何大小為 *n* (必須比 *n0* 大)的輸入,它至多需要 5*n*3 + 3*n* 的時間執行完畢,那麼它的漸近時間複雜度是 O(*n*3).
## 二、時間頻度
要理解時間複雜度,需要先理解時間頻度,而時間頻度簡單的說,就是**演算法中語句的執行次數**。
舉個例子:
要計算1+2+...+100,現在有兩種演算法
~~~java
public int fun1(int n){
int total;
for(int i = 0; i <= n; i++){
total+=i;
}
return total;
}
public int fun2(int n){
int total = (1 + n)*n/2;
return total;
}
~~~
我們可以看見,對於`fun1()`這個方法,不管n多大,永遠需要執行n+1次,也就是說他的時間頻度是T(n)=n+1,
而對與`fun2()`來說,不管n多大都只需要執行1次,所以他的時間頻度T(n)=1。
**當n趨向無窮大時,有三個忽略**:
### 1.忽略常數項
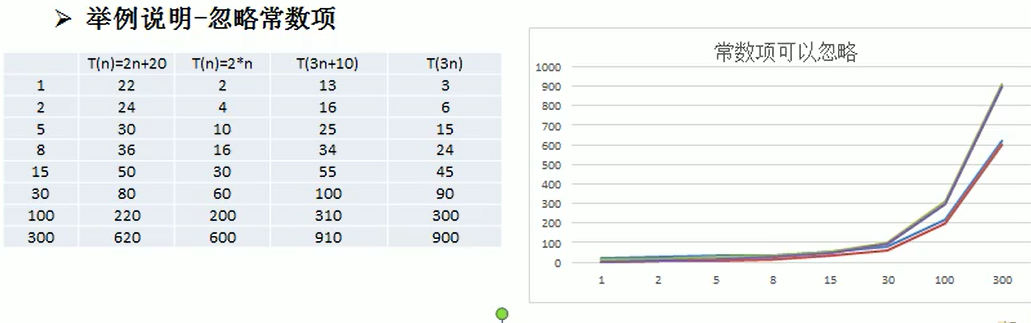
比如T(n)=2n+1,當n趨向無窮大時,可以忽略常數項1;
參見下圖:
- 2n+20 和 2n 隨著n 變大,執行曲線無限接近, 20可以忽略
- 3n+10 和 3n 隨著n 變大,執行曲線無限接近, 10可以忽略
### 2.忽略低次項
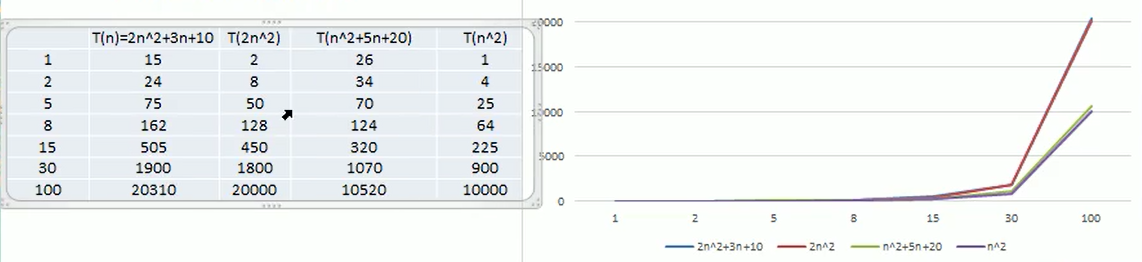
比如T(n)=2n+3n^8,當n趨向無窮大時,可以忽略低次項及其係數2n;
參見下圖:
- 2n^2+3n+10 和 2n^2 隨著n 變大, 執行曲線無限接近, 可以忽略 3n+10
- n^2+5n+20 和 n^2 隨著n 變大,執行曲線無限接近, 可以忽略 5n+20
### 3.忽略係數
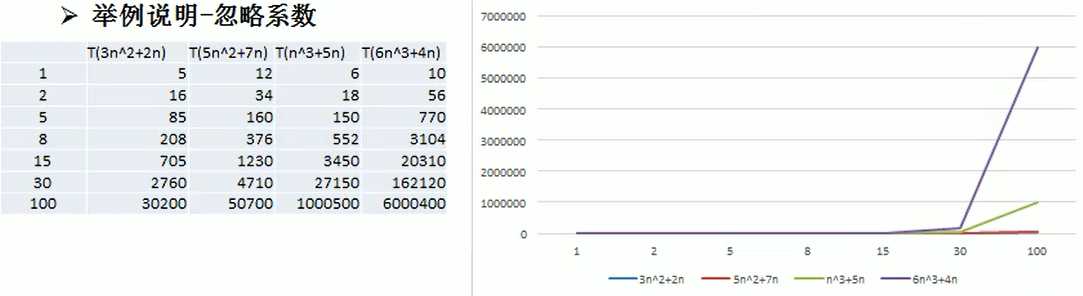
比如T(n)=2n^8,當n趨向無窮大時,可以忽略係數2。
參見下圖:
- 隨著n值變大,5n^2+7n 和 3n^2 + 2n ,執行曲線重合, 說明 這種情況下, 5和3可以忽略。
- 而n^3+5n 和 6n^3+4n ,執行曲線分離,說明多少次方式關鍵
## 三、時間複雜度
我們現在理解了時間頻度的T(n)的含義,假設當有一個輔助函式f(n),使得**當n趨近無窮大時**,T(n)/f(n)的極限值為不等於0的常數,就叫f(n)為T(n)的同量級函式,記作T(n)=O(f(n)),
稱O(f(n))為演算法的**時間漸進複雜度**,也就是**時間複雜度**。
又根據時間頻度T(n)的“三個忽略”原則,我們可以知道時間複雜度是這樣得到的:
1. 忽略所有常數
2. 只保留函式中的最高階項
3. 去掉最高階項的係數
舉個例子:
某演算法T(n)=2n^3+4n-5,按步驟走:
1. T(n)=2n^3+4n
2. T(n)=2n^3
3. T(n)=n^3
即可得該演算法時間複雜度為O(n^3)
## 四、常見時間複雜度
這裡按複雜度從低到高列舉常見的時間複雜度:
1. 常數階O(1)
~~~java
// 無論程式碼執行了多少行,只要是沒有迴圈等複雜結構,那這個程式碼的時間複雜度就都是O(1) 。
public void fun(int n){
n+=1;
}
~~~
2. 對數階O(log2n)
~~~java
// 根據公式有 n = 2^x,也就是 x = log2n,x即為迴圈程式碼執行次數,所以時間複雜度為O(log2n)
public void fun(int n){
int i = 1;
while(i < n){
i = i *2
}
}
~~~
3. 線性階O(n)
~~~java
// 一般來說,只要程式碼裡只有一個迴圈結構,即輸入規模和執行次數呈線性相關,那這個程式碼的時間複雜度就都是O(n) 。
public void fun(int n){
for(int i = 0; i < n; i++){
n+=i;
}
}
~~~
4. 線性對數階O(nlogn)
~~~java
// 可以簡單理解為對數階的程式被放入了迴圈結構中,也就是n*O(logn),下面的程式碼的複雜度就是O(nlog2n)
public void fun(int n){
int j = 1;
for(int i = 0; i < n; i++){
while(i < n){
j = j *2
}
}
}
~~~
5. 平方階O(n²),立方階O(n^3),K次方階O(n^k)
~~~java
// 平方階可以簡單理解為線性階中巢狀一個線性階,也就是O(logn)*O(logn),下面的程式碼複雜度就是O(n^2)
// 立方階同理,就是三個線性階的巢狀,K次方階同理
public void fun(int n){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; i++){
i=i+j;
}
}
}
~~~
## 五、複雜度的四個概念
1. 最壞情況時間複雜度:程式碼在最理想情況下執行的時間複雜度。
2. 最好情況時間複雜度:程式碼在最壞情況下執行的時間複雜度。
3. 平均時間複雜度:用程式碼在所有情況下執行的次數的加權平均值表示
4. 均攤時間複雜度:在程式碼執行的所有複雜度情況中絕大部分是低級別的複雜度,個別情況是高級別複雜度且發生具有時序關係時,可以將個別高級別複雜度均攤到低級別複雜度上。基本上均攤結果就等於低級別複雜度。
舉個例子:
長度為n的陣列查詢一個給定元素k
~~~java
public void fun(int[] arr,int k){
for(int i = 0; i < arr.length; i++){
if(arr[i] == k){
//找到了
}
}
}
~~~
上面這個方法,最好的情況下元素k就在陣列第一位,複雜度為O(1),但是最壞的情況下,元素k在陣列最後一位,複雜度為O(n)。
同一段程式碼在不同情況下時間複雜度會出現量級差異,為了更全面,更準確的描述程式碼的時間複雜度,我們引入這4個概念,當然,在大多數時候我們是不用特意區分這四種情況的。
## 六、總結
總結一下如何快速判斷程式的時間複雜度:
- 只關注迴圈最多的那部分程式碼
- 總複雜度等於量級最大的那段程式碼的複雜度
- 巢狀程式碼的複雜度等於巢狀內外程式碼複雜度
