網路流初步
阿新 • • 發佈:2020-07-10
#### 以下內容均以[此題](https://www.luogu.com.cn/problem/P3376)為例講解,以下貼的程式碼,都不能過,long long這些東西自己改,全部用int感覺美觀一些
------------
## 網路流
那麼做這道模板題之前還是先了解一下網路流到底是個什麼吧(因為我也是個初學者,如果有講錯或者不清楚的地方可以評論或者在其他dalao的題解或是部落格中學習)
對於一個**網路** $G=(V,E)$ 是一個**有向圖**,每一條邊有一個邊圈 $c(x,y)$ 表示這條邊的**容量**,你可以把它想象成一個下水道系統(???),每一條邊都是一個管道,每個管道有自己允許流通的水的**最大值**。對於兩個特殊節點, $S$ 和 $T$ ($S$ ≠ $T$),如果有 $S\in G$ 且 $T\in G$,稱$S$為**源點**, $T$ 為**匯點**,所有水從 $S$ 流向 $T$
形如以下這個圖:
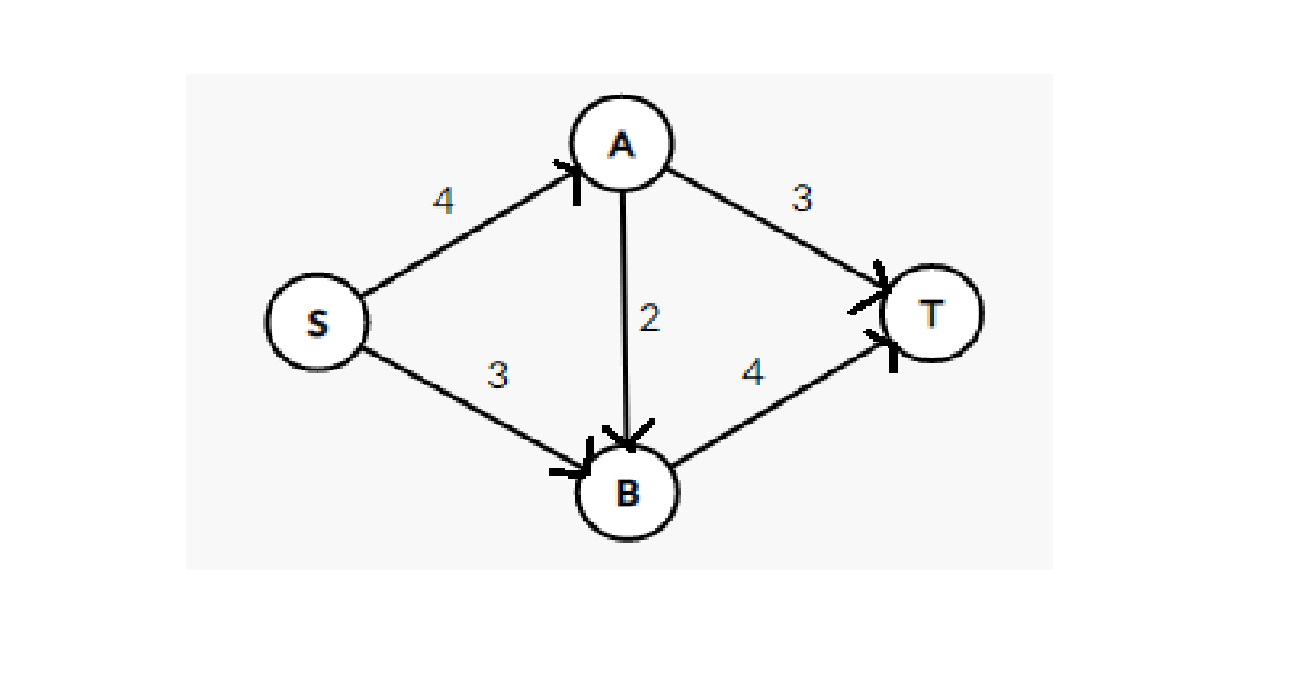
那麼 $S->A->B->T$ 就是該網路的一個流,這個流的流量為2(該路徑上的最小的容量)
那麼對於這個流量,應該如何定義呢?我們引入一個流函式(摘自李煜東的《演算法進階》)
$f(x,y)$為定義在節點二元組($x$∈$V$,$y$∈$V$)上的實數函式,滿足:
1. $f(x,y)$ ≤ $c(x,y)$
2. $f(x,y)$ = $-f(y,x)$
3. $\forall$ $x$≠$S$,$x≠T$, $\sum_{(u,x)∈E }f(u,x)=\sum_{(x,v)∈E }f(x,v)$
$f$稱為該網路的流函式,對於$(x,y)$∈$E$,$f(x,y)$為邊的流量,$c(x,y)-f(x,y)$為該邊的剩餘容量
這三條性質分別為**容量限制**,**斜對稱**和**流量守恆**。其中流量守恆告訴我們只有源點和匯點才會儲存流,其流入總量等於流出總量
------------
## 最大流
對於一個網路,有很多的流函式$f$都是合法的,那麼使得整個網路的$\sum_{(S,v)∈E }f(S,v)$最大的流函式稱為該網路的**最大流**,此時的流量為該網路的**最大流量**
那麼求這個最大流,我會講解 **Edmonds-Karp**增廣路演算法 和 **Dinic**演算法,當然還有**ISAP**和**HLLF**等更加高效的演算法,因為蒟蒻不太會,這裡就不介紹,如果學會了會更新的
### **Edmonds-Karp**增廣路演算法
時間複雜度:$O(nm^2)$
先介紹一下**增廣路**是個什麼:對於 $S$ 到 $T$ 的一條路徑,如果路徑上各邊的剩餘容量大於0,則這一條路徑就是一條增廣路
那麼仔細一想,如果當前網路中還存在著那麼一條增廣路,那麼說明我的流量還可以更大(見增廣路的定義和剩餘容量的定義),那麼EK演算法的核心思想就是不斷地尋找增廣路,直到無法找出最廣路之後,說明找出了網路中的最大流
那麼注意在實現尋找增廣路時,我們可以用廣搜實現,這樣就可以保證找到每一條增廣路
那麼在找到增廣路時,我們也應該去考慮反向邊,用來反悔,也就是還原。在找到一條增廣路時,路徑上的容量應該減去這條增廣路的流量,那麼在處理這個東西之後就會影響到其它增廣路,這個時候建反向邊就可以起到一個反悔的作用
那麼整個的模擬過程如下(從左往右看):

那麼我們就可以寫出來第一份程式了
```
#include q;
q.push(s);
v[s]=true;
minn[s]=INF;
while(!q.empty()){
int x=q.front();
q.pop();
for(register int i=head[x];i;i=e[i].net){
if(e[i].w!=0){ //不為0才走
int y=e[i].to,z=e[i].w;
if(v[y]==true) continue; //增廣路走過就不管了
minn[y]=min(minn[x],z);
bian[y]=i;
v[y]=true;
q.push(y);
if(y==t) return true; //可以到達匯點
}
}
}
return false;
}
void update(){
int x=t;
while(x!=s){
int i=bian[x];
e[i].w-=minn[t]; //正向邊-
e[i^1].w+=minn[t]; //反向邊+
x=e[i^1].to;
}
//這個異或1其實非常的秒
//因為之前在儲存邊的時候,是直接正向反向一起存
//所有反向邊=正向邊+1
//一個偶數異或1=偶數+1
//一個奇數異或1=奇數-1
ans+=minn[t]; //更新答案
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(register int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z); //有向邊儲存
add(y,x,0); //先存一個邊權為0的反向邊,有用
}
while(bfs()==true) update(); //不斷更新增廣路
printf("%d",ans); //答案
return 0;
}
```
出題人毒瘤地卡掉了EK,但其實EK是能過的(想不到吧嘿嘿嘿),TLE的那兩個點其實是因為有太多的重邊,那麼其實對於重邊,我們只需要將重邊累加,也可以AC的(@那一條變阻器,他用vector這麼過的),其實在上面的程式的基礎上改不了多少東西,就兩行
```
#include q;
q.push(s);
vis[s]=1;
dis[s]=2005020600;
while(!q.empty()) {
int x=q.front();
q.pop();
for(register int i=head[x];i;i=e[i].net) {
if(e[i].val==0) continue;
int v=e[i].to;
if(vis[v]==1) continue;
dis[v]=min(dis[x],e[i].val);
pre[v]=i;
q.push(v);
vis[v]=1;
if(v==t) return 1;
}
}
return 0;
}
inline void update() {
int x=t;
while(x!=s) {
int v=pre[x];
e[v].val-=dis[t];
e[v^1].val+=dis[t];
x=e[v^1].to;
}
ans+=dis[t];
}
int main() {
scanf("%d%d%d%d",&n,&m,&s,&t);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u,&v,&w);
if(flag[u][v]==0) {
add(u,v,w);
flag[u][v]=tot; //用一個數組記錄這一條邊
}
else {
e[flag[u][v]-1].val+=w; //累加重邊
}
}
while(bfs()!=0) {
update();
}
printf("%d",ans);
return 0;
}
```
### **Dinic**演算法
時間複雜度: $O(n^2m)$
相對於之前EK演算法來說,在稀疏圖中的表現其實是差不多的,但是在稠密圖中就快很多了,別妄想這總用第二個程式過,還是要學學一些更加優秀的演算法(所以我為什麼還不學ISAP之類的)
講Dinic之前,我們不妨再引入一個東西:**殘量網路**。任意時刻,在網路中所有節點以及剩餘容量大於0的邊構成的子圖叫做殘量網路。在EK演算法中,每輪BFS會遍歷整個殘量網路,但只更新一條增廣路,這就浪費了很多時間,就需要用Dinic演算法了
我們設一個 $d[x]$ 表示 $x$ 的層次,如果滿足$d[y]=d[x]+1$ 的邊$(x,y)$,則它是一個分層圖,是一個有向無環圖
為什麼用Dinic會更優呢,我們先用BFS求出每一個節點的深度,在分層圖上DFS只去尋找到下一層的邊,每一次找出多條增廣路,這樣就會快很多,但是BFS會跑很多遍,ISAP只用跑一遍,但是我不會(菜)
這其中還會涉及一個**當前弧優化**,聽著很nb是吧,就是在更新第$i$條邊時,前面$i-1$條邊到匯點的流已經流蠻並且沒有路可以走了,可以不去更新,我們記錄一下就可以了,不需要重新去跑之前的邊
至於實現的方法,直接在程式碼中講解好了:
```
#include q;
for(register int i=1;i<=n;i++) de[i]=INF;
q.push(s);
de[s]=0;
now[s]=head[s]; //充分發揮一個作為副本的作用
while(!q.empty()){
int x=q.front();
q.pop();
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(z!=0&&de[y]==INF){ //如果當前邊可以走且還沒找過
q.push(y);
now[y]=head[y];
de[y]=de[x]+1; //更新層次
if(y==t) return true;
}
}
}
return false;
//其實和EK的BFS差不了多少的
}
int dfs(int x,int liu){
if(x==t) return liu; //直接返回
int k,ans=0; //k是當前最小的剩餘容量,
for(register int i=now[x];i&&liu;i=e[i].net){
now[x]=i;//當前弧優化
int y=e[i].to;
if(e[i].w!=0&&(de[y]==de[x]+1)){
k=dfs(y,min(liu,e[i].w)); //比較出一條更小的
if(!k) de[y]=INF; //剪枝,去掉增廣後的點
e[i].w-=k;
e[i^1].w+=k; //正向反向更新
ans+=k; //流出去的流量和
liu-=k; //剩餘流量減少
}
}
return ans;
}
int main(){
scanf("%d%d%d%d",&m,&n,&s,&t);
tot=1;
for(register int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,0);
}
int maxx=0; //最大流
while(bfs()) maxx+=dfs(s,INF);//記錄答案
printf("%d",maxx);
return 0;
}
```
感謝一下@那一條變阻器和@取什麼名字 兩個大佬的指點,當然還有其他題解(因為我最開始自己也不會編
