小編在市面看了很多介紹計算機視覺的知識，感覺都非常深奧，難以理解和入門。因此總結出了一套容易理解的教程，希望能夠和大家分享。

一.人工神經網路

人工神經網路是一種模擬人腦構建出來的神經網路，每一個神經元都具有一定的權重和閾值。僅有單個神經元的圖例如下所示：

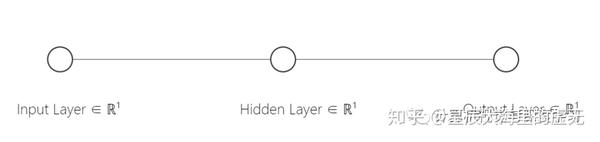
從中可以看到每一個神經元具有一個輸入Input Layer，一個輸出Ouput Layer。一般情況下，Input Layer僅有一個數值，Output Layer也僅是一個數值。中間的Hidden Layer則負責運算。而這個運算的過程我們使用了Sigmoid函式。這個函式是什麼意思呢？假設我們輸入的一個數值小於了某個閾值，那麼神經網路的Output輸出為0，大於這個閾值則輸出1。而怎麼在計算機當中用函式實現這個過程呢？科學家所構想的Sigmoid函式可以滿足這一點，有了函式就可以將其放入到計算機當中進行運算啦！如下圖所示。Hidden Layer當中的神經元就做如下的Sigmoid的運算，橫座標為輸入Input Layer的值，縱座標則代表Output Layer的值。

圖1 Sigmoid function

我們可以從中看到，只要我們的輸入值（橫座標）大於了5，輸出值就十分逼近1，而小於了-5則十分逼近0，橫座標0是一個閾值（分界線）。這個函式的表示式在上圖中也已經寫出，也就是sigma(z)=1/(1+exp(-z))。這就是單個神經元之間是如何運算的方法，我們瞭解了單個神經元當中是如何運算的，就可以將其擴充套件到多個神經元了。

二.全連線神經網路

神經網路當中最基礎的就是全連線神經網路了，在全連線神經網路每一層當中的一個神經元就與下一層的所有神經元都相連。神經網路可以分為輸出層，輸出層，和隱藏層，用於輸入資料的層就是輸入層，輸出資料的是輸出層，中間的所有層都叫做隱藏層。可以用下圖來表示：

圖 2 ：全連線神經網路

在這個全連線神經網路當中，一共具有四個輸入的值，因此第一個Input Layer具有四個點，中間則為Hidden Layer隱藏層，這裡設定了五個神經元，最後Output輸出層具有一個值。那麼像這種類似的全連線神經網路可以做什麼呢？就連這樣一個簡單的神經網路，稍作修改，用於做手寫數字數字0-9的識別準確率就能夠達到百分之97左右。對於識別手寫數字而言，我們採用Mnist資料集，在這個資料集當中，每一幅數字的圖片的分別率都是28*28，也就是一張圖片上具有28*28個小方格，影象的長度為28個小方格，寬度也為28個小方格。每一個小方格上具有一個0-255之間的數字，這個數字代表了從黑色到白色的程度，0代表純黑，255代表純白。因此我們想要把數字輸入到神經網路當中，也就是把這些小方格所對應的數字輸入到神經網路當中，因此我們將輸入層從剛才圖中的4個，更改為28*28個，每一個節點用於接收一張手寫數字圖當中的一個小方格當中的數字，中間的隱藏層我們設定為30個神經元，輸出設定為10個輸出，因為有0-9一共十個數字，10個輸出當中的其中一個輸出都代表了識別為這個數字的概率。我們通過這個神經網路進行訓練，通過使用Pytorch，Tensorflow等框架編寫的程式碼，用Java實現可以使用DJL，或者在Java當中呼叫OpenCV即可。只要編寫好這些神經網路每一層的架構，這個神經網路就會自動更新每一個神經元的權重，通過更新權重將最後輸出的概率逼近於真實輸入到神經網路當中的數字。

比如我們輸入手寫數字“1”，在輸出層負責輸出是否為數字“1”的神經元則會輸出0.95，表示這個數字為1的概率為0.95，而其他輸出層神經元的輸出概率之和則為1-0.95=0.05。這就是全連線神經網路的作用了，目前還沒有具體的理論能夠解釋究竟是為什麼像這種神經網路的結構能夠對數字進行識別達到如此高的準確度，但我們知道如果隱藏層所使用的神經元越多，隱藏層的層數越多，那麼模型預測的精度就會越來越高，越大的神經網路也越容易訓練。後來經過實驗表明，在全連線層當中加入卷積神經網路層更能夠增加神經網路識別的準確度，因為卷積神經網路的影象當中的特徵提取能力會比全連線神經網路更強。

三.卷積神經網路

由於卷積神經網路對影象特徵提取的能力會更強，在很多領域全連線神經網路並不是很管用，比如對一些更大的圖片，圖片當中並不是形狀單一的數字，而是形形色色的動物，比如馬，貓，狗等等。計算機要想對這些挑戰性更大的圖片進行識別，因此需要對圖片特徵進行一個更為有效的提取。根據實驗證明，卷積神經網路能夠很好地提取圖片的特徵，並對影象進行識別分類。為了更好的學習卷積神經網路，我們先介紹一些有關影象的知識。

在一般情況下影象是灰度圖，也就是隻有一個通道的黑白影象，一個影象只有一層。而對於彩色影象而言，一般具備三個通道，分別是紅，黃，藍三個通道，只要把這三個通道（可以理解為三層影象）疊加在一起，就可以在每一個畫素點上顯示出其他的顏色，因為所有的顏色都可以由紅，黃，藍這三個顏色組成。一張4*4的具有三個通道的彩色影象如下所示：

圖3 ：RGB影象

在這張圖上的每一個小方格都具有一個0-255之間的數值，代表了顏色的深度。卷積神經網路如果想要對這張彩色的影象進行處理，其實也比較簡單。卷積神經網路當中每一層都具有一個或者多個卷積核，我們先討論僅有一個卷積核的情況。卷積核可以看作是一張僅有一個通道的圖片，它的大小可以為為3*3，4*4，5*5等等。我們一般取3*3大小的作為我們的卷積核，也就是kernel size=3。那麼卷積操作是如何進行的呢？卷積核如下圖所示：

圖4：卷積核

在卷積神經網路當中我們經常聽到感受野這個學術詞彙，感受野其實就是卷積核的大小，這兩者之間並沒有區別，只是換了一個說法而已。那麼神經網路層之間的卷積是怎麼進行操作的呢？假設我們的卷積核就採用上圖當中的卷積核，對於需要進行卷積計算的圖片為一張大小為5*5的灰度圖片（並非RGB具有三通道的圖片，這裡僅僅只有一個通道）。我們讓這個3*3的卷積核依次從左到右掃描過這張5*5的影象，掃描完一行之後再切換到下一行進行掃描，每掃描依次就做矩陣內積計算，使用這種方法計算出卷積之後的數值。在正常的卷積操作當中，卷積核的大小比影象的大小會更小，這樣卷積核才能夠在影象當中進行掃描，得到有效的資訊。在最初還沒有深度學習的時代，電腦科學家通過經驗調整卷積核當中的數值，這樣就可以進行各種各樣的影象處理操作，只要稍微調整卷積核當中的數值，就可以在掃描完影象一次之後，將影象變模糊，或者在卷積完之後只保留影象當中物體的邊緣。下面是卷積操作的具體過程：

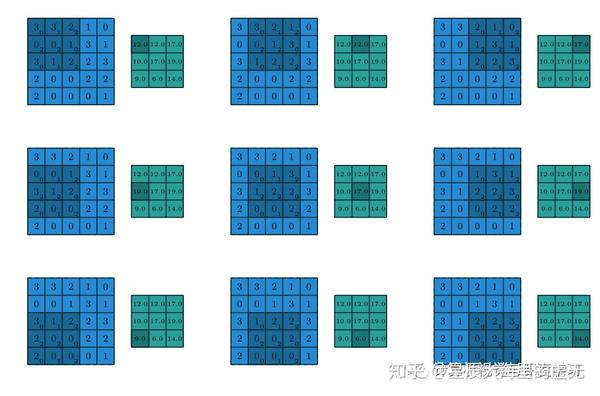
圖 5：卷積操作的實現

如上圖所示，該圖出自於論文《A guide to convolution arithmetic for deep learning》當中。這個卷積核在一個5*5的影象上不斷掃描，輸出了一個3*3的影象。這個影象上的數值是怎麼通過矩陣內積計算出來的呢？很簡單，在第一張圖當中，我們的卷積核正好在覆蓋在這幅圖的左上方，覆蓋到的影象裡的數字依次為3，3，2，0，0，1，3，1，2。卷積核當中的數字則是0，1，2，2，2，0，0，1，2。內積操作則是將所有在空間上位置一致的數字對應相乘，再全部相加。卷積核當中的第一個數字和影象當中的第一個數字分別為3和0，因此相乘等於0。第二個小方格的乘積為3*1=3，然後計算出每一個小方格的乘積，最後將這些計算出來的乘積全部相加得到輸出3*3影象當中的第一個數值。第一步計算的過程是：3*0+3*1+2*2+0*2+0*2+1*0+3*0+1*1+2*2=12。因此輸出影象當中的第一個的數值為12，以此類推。在深度學習當中，卷積核當中的數字並非程式設計人員直接設定，而是通過這樣的卷積神經網路訓練出來的數值。

可能你會覺得疑惑，為什麼卷積神經網路是一個網路呢，裡面的操作並沒有像全連線神經網路一樣表示出來啊？也沒有在剛才的操作當中看到一個網路啊？道理很簡單，我們只需要把一個二維的影象展平，就變成了一個一維的網路，這樣就可以作為輸入直接將影象的資訊“喂”到一個卷積神經網路裡了。

卷積神經網路當中還有一個比較神奇的地方則是，假設我們輸入的影象是一個3*3，具有三通道的RGB影象又該怎麼辦呢？是不是應該一張圖想配備上三個卷積核呢？答案是：No！我們依然只需要一個卷積核就可以對這個三通道的RGB影象進行處理。只是在滑動卷積核的同時，要同時對三層影象做內積。也就是首先通過卷積計算出每一層的數值，再把這三層的所有數值都相加，就得到輸出的數值。因此即使我們有三層影象的輸入，最後得到也只是一個一維的影象。但我們也可以通過設計卷積核從而得到多個維度的影象，每一個卷積核都會掃描原圖當中的所有部分從而得到一個輸出維度(影象)，我們想要輸出多少個維度的影象，在卷積神經網路裡設定多少個卷積核即可。

下面我們再來介紹一下卷積神經網路的引數。第一個也就是stride了，這個引數的中文含義是步伐，也就是卷積核在掃描影象時每掃描一次，是向右移動一步還是向右移動兩步，三步等等。我們來看一個例子，在這個卷積操作當中，stride=2，用來做卷積操作的影象的大小依然為5*5，卷積核的大小為3*3，我們來看看這個怎麼完成的：

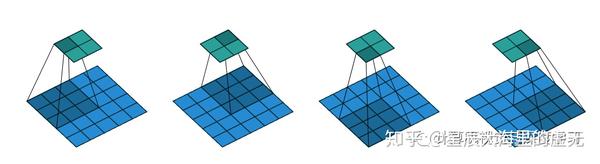
圖 6：strde=2的卷積

在上面這張圖中，輸入的影象在最下方，而輸出的影象在最上方。我們每移動一次卷積核就跳過了兩個小方格，不管是從左向右移動還是從上往下運動，都跳過了兩個小方格，因此我們的輸出才是一個2*2的小方格。如果此時的stride設定為3，那麼我們只會得到一個輸出，因為卷積核不會因為stride太大就跳出原影象進行掃描。在stride為3的情況下我們只有增大原影象的大小才能夠得到一個具有更多數字輸出的影象。

四.影象的池化

在學習了神經網路和卷積神經網路的基礎知識之後，我們就可以開始學習影象池化這一激動人心的知識了！在影象識別領域，世界上一些聰明的研究人員設計了不少效果相當不錯的神經網路，比如 Alex Net, VGG, Google Net, ResNet等等。那麼它們是怎麼被設計出來的呢？

我們繼續剛才的內容，深入瞭解一下卷積神經網路。在卷積神經網路當中，我們不僅僅有卷積的操作，還有一種叫做池化操作，這些影象識別的神經網路無非就是使用卷積操作和池化操作不斷地重複，然後實驗，調參，最後就可以設計出一個神經網路用於影象識別了！池化操作比卷積操作更加簡單，一般情況下我們用到的有平均池化，還有最大池化。假設我們有一個4*4的影象，如下所示：

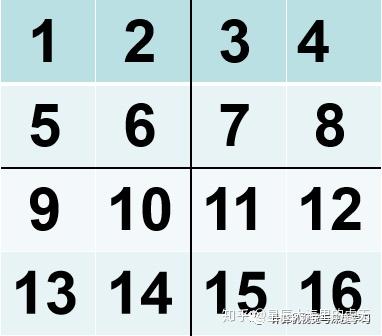
圖7：池化影象

如果我們將其進行2*2的最大池化，也就是將這個4*4的影象分解成多個小的部分，每一部分都是一塊2*2的小影象。在每一塊2*2的影象當中取出一個最大的數值，這就是最大池化。在上圖當中，第一小塊影象的最大數值是6，第二塊是8，第三塊是14，第四塊是16。因此做了最大池化之後輸出的結果圖如下所示：

圖8：池化之後的輸出

如果將影象做3*3的池化，也就是將影象全部分解成大小為3*3的小影象。然後根據是平均池化還是最大池化求出每一個輸出小方格的值，平均池化就是把這個3*3的小影象求出平均值用於輸出即可，之前我們這裡沒有提到。那麼什麼是用於影象識別的網路呢？

五.影象識別

影象識別技術是所有計算機視覺技術的基石，不管是目標檢測，影象語義分割，目標跟蹤,，ocr文字識別等等都需要影象識別技術作為基礎。影象識別技術主要用於影象的分類，比如我們有一大堆已經標註好的貓貓和狗狗的影象，我們怎麼讓計算機也知道這些影象是貓貓還是狗狗呢？從計算機視覺的革命開始之時，Yun lecun在二十年前，也就是在1998年就提出的一種名叫LeNet的卷積神經網路用於數字分類，可以識別從0-9的數字。我們用這種卷積神經網路可以達到99.4%的識別準確率，在當時已經是像神一樣的存在了，這個結果甚至比人類對驗證碼識別的準確率還要高。之前的全連線神經網路最多能夠達到97%左右的準確率，但是越往上面走，連提升一個百分點都非常困難，那麼這個神經網路的構造是什麼樣的呢？

圖9：LeNet5 卷積神經網路架構
我們的輸入層，是一系列32*32的手寫字型圖片，這些手寫字型包含0~9數字，相當於10個類別的圖片輸出的結果是分類的結果，也就是0~9之間的所數所預測得到的概率值。在我們訓練時，只能夠把影象一張一張地送進神經網路，每一張影象都是32*32，因此這個神經網路的輸入神經元有32*32=1024個。接著第二層就進入了我們的卷積神經網路層，在論文當中採用了6個卷積核，每一個卷積核的大小為5*5.然後進行最大池化，將輸出的Ouput的大小減半，之後又對池化的結果做卷積操作，卷積核依然選擇5*5，但是這時使用了16個卷積核，因此會輸出16個通道的圖片，我們可以將通過卷積操作之後的影象稱之為特徵圖(Feature Map)。然後再做最大池化，將特徵提取得更加抽象，池化之後又卷積。最後經過雙層全連線神經網路，第一層全連線層具有128個神經元，第二層有84個神經元，這些具體神經元的個數都是調參和實驗的結果，最後得到10個輸出，代表了每個數字所輸出的概率。這樣，LeNet-5就設計完成了。當然，後續的研究者參照LeNet-5的研究思想又發明了其他的神經網路，後來發明的神經網路則可以用來做任意物體的影象分類，這些新發明為如今如火朝天的計算機視覺技術奠定了巨大的基礎。

今天小編的分享就到這裡啦！

終於寫完啦，如果覺得讀了小編的文章您有收穫的話，不要忘記了點選下方的“推薦”哦！您的支援就是對小編創作最大的動