誰說有序連結串列不能進行二分查詢,只是需要進化而已?!
阿新 • • 發佈:2020-09-07
# 前言
> 本文收錄於專輯:[http://dwz.win/HjK](http://dwz.win/HjK),點選解鎖更多資料結構與演算法的知識。
你好,我是彤哥。
上一節,我們一起學習了關於雜湊的一切,特別是雜湊表的進化過程,相信通過上一節的學習,你一定可以從頭到尾完整地給面試官講講雜湊表是如何發展到如今這一步的。
但是,難道HashMap的終極形態只能通過“陣列+連結串列+紅黑樹”的形式實現嗎?有沒有可替代方案?為什麼Java沒有使用你說的這種替代方案呢?
本節,我們就來學習另外一種資料結構——跳錶,關於跳錶的內容,我將分成兩節完成,第一節介紹跳錶的演進過程,第二節程式碼實現跳錶,並改寫HashMap。
好了,讓我們先進入跳錶第一小節的學習。
# 有序陣列
大家都知道陣列是可以支援隨機訪問的,也就是通過下標可以快速地定位到元素,時間複雜度是O(1)。
那麼,這個隨機訪問的特性除了根據下標查詢元素,還具有哪些用處呢?
試想,如果一個數組是有序的,我要查詢某個**指定的元素**,如何才能做到最快速地查找出來呢?

簡單地方法,從頭開始遍歷整個陣列,遇到了要查詢的元素就返回,比如,查詢8這個元素,要走6次才能查詢到,要查詢10這個元素更誇張,需要8次。
所以,這種方式的查詢元素的時間複雜度為O(n)。

快速地方法,因為陣列本身是有序的,所以,我們可以使用二分查詢,先從中間開始查詢,如果指定元素比中間的元素小,再在左半邊查詢,如果指定元素比中間元素大,則在右半邊查詢,依次進行,直到找到指定元素。比如,查詢8這個元素,先定位到中間(7/2=3)的位置,下一次查詢讓左指標加1,把4號位置作為左指標,中間的位置變為(4+(7-4)/2=5)的位置,查詢到8這個元素,一共只需要2次。
使用二分查詢,效率提升了不止一星半點,即使最壞的情況也只需要log(n)的時間複雜度。

# 有序連結串列
上面我們介紹了有序陣列的快速查詢,下面我們再來看看有序連結串列的情況。

上面是一個有序連結串列,此時,我要查詢8這個元素,只能從連結串列頭開始查詢,直到遇到8為止,時間複雜為O(n),似乎沒有什麼更好地辦法了。

讓我們考慮有序陣列和有序連結串列的不同之處,有序陣列之所以能夠實現可以直接定位到中間元素,得意於其可以通過索引(下標)快速訪問的特性,那麼,我們給有序連結串列加上索引是不是就可以實現類似的功能了呢?
答案是肯定的,這種具有索引的有序連結串列就是跳錶,下面有請跳錶登場。
# 跳錶
**第一個問題:怎麼給有序連結串列加索引呢?**
這裡,需要增加一個“層”的概念,假設原始連結串列的層級為0,那麼,在其中選擇一些元素向上延伸,形成第1層索引,同樣地,在第1層索引的基礎上,再選擇一些元素向上延伸,形成第2層索引,直到你覺得索引的層數差不多了為止,沒錯,跳錶就是這麼隨意,你滿意就好^^
假設,針對上面的有序連結串列,我加了這麼一些索引:
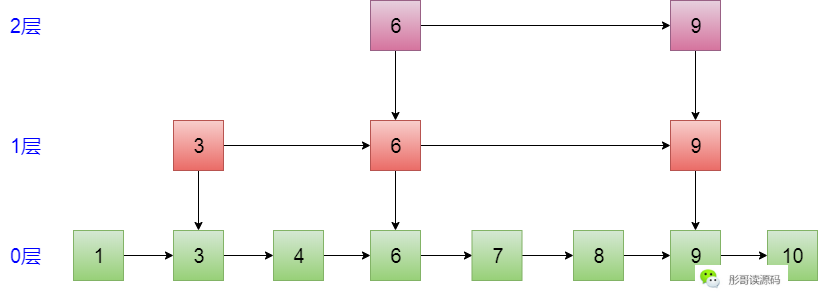
**第二個問題:從哪開始訪問這個跳錶呢?6?3?1?9?**
好像都不行,所以,還要增加一個特殊的節點——頭節點,放在0號元素的前面,比如,上面的跳錶增加頭節點之後的樣子如下:
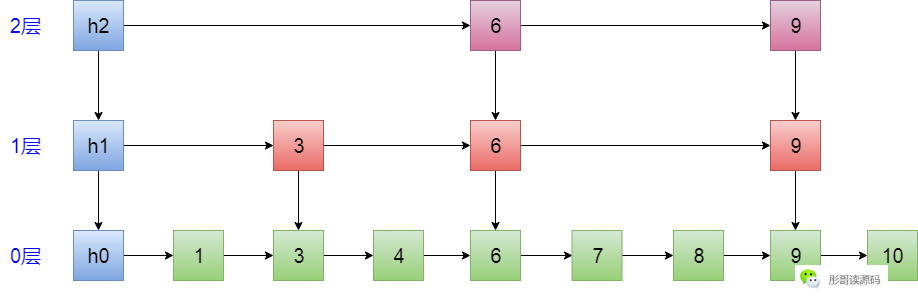
此時,只要從h2這個節點開始,就能很快速地查詢到跳錶中的任意一個元素。
比如,要查詢8這個元素,h2先向右看一下,咦,是6,比8小,跳到6這個位置,再向右看一下,啊,是9了,比8大了,所以,不能跳過去,向下跳一步,跳到第1層6的位置,向右看一下,又是9,不能跳過去,再向下跳一步,到第0層的6,既然,到第0層,那隻能按照連結串列依次往後遍歷了,直到遇到8為止,整個過程如下:
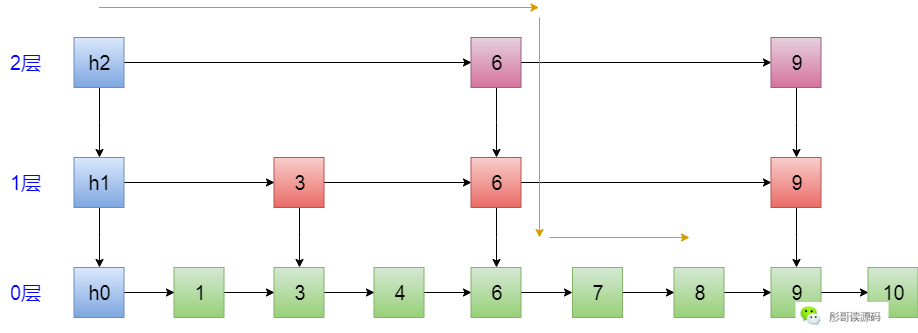
可以看到,整個過程就是跳呀跳呀跳,所以得名——跳錶。
這裡的元素個數比較少,可能還看不出太大的優勢,試想,如果元素非常多,每兩個元素向上形成一個索引,每兩個索引再向上形成一個索引,最後,就類似於一顆平衡二叉樹了:
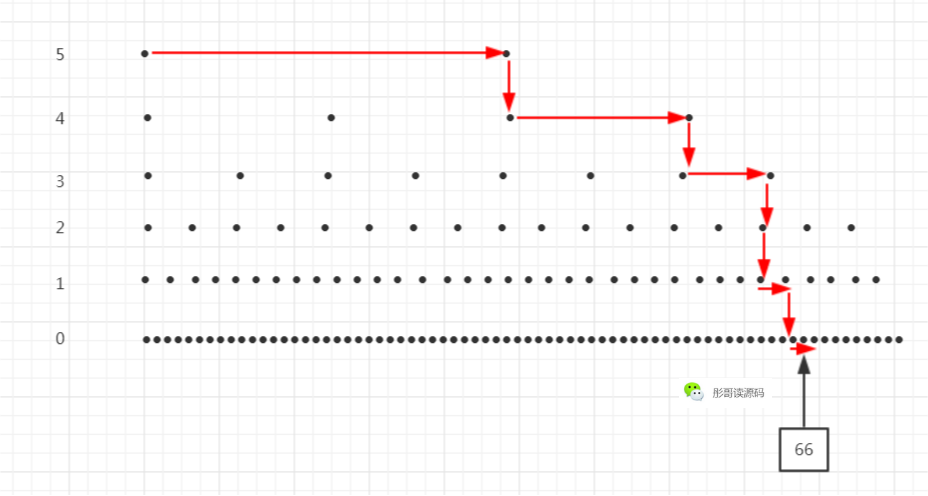
可以看到,每次查詢可以減少一半的搜尋範圍,所以,跳錶的查詢時間複雜度為O(log n)。
但是,實際情況是不可能使用這種完全平衡的跳錶的,因為,如果要保持平衡的特性,在插入元素或刪除元素的時候勢必需要做再平衡的操作,這樣就大大地降低了效率,所以,一般地,我們使用隨機來決定一個元素或者索引要不要產生索引。
**第三個問題:索引何時產生呢?**
最好的時機莫過於插入元素的時候,因為在插入元素之後的下一步就要立馬使用索引了,為什麼這樣說呢?因為不管是插入、刪除還是查詢,其實,都要先走查詢找到那個元素才能進行下一步操作。說白了,就是不管什麼操作,都要查詢,是查詢就要走索引,要走索引就要先建索引,要建索引那就在插入元素的時候。
OK,下面我將使用一步一圖的方式,帶你領略跳錶建立的完整過程:
1. 初始狀態,只有一個頭節點h0(不,還有一個彤哥讀原始碼的水印,調皮^^)。

2. 插入一個元素4,放在h0後面,並隨機決定要不要向上形成索引,結果是不形成索引。

3. 插入一個元素3,從h0開始查詢,h0的下一個元素是4,比3大,所以,3放在h0和4之間,然後詢問要不要形成索引,隨機決定說要形成索引,此時,3向上形成索引,同時,h0也要向上形成索引h1,結果如下:
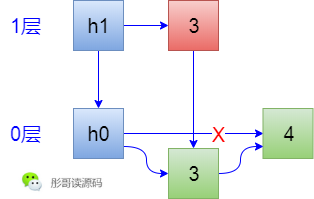
4. 插入一個元素9,從h1開始查詢,依次經過h1->3->3->4,都沒有找到位置,最後插入到4後面,並詢問要不要形成索引,隨機決定說我要形成索引,而且我要形成2層索引(最多比當前層數多1),然後就變成了這個樣子:
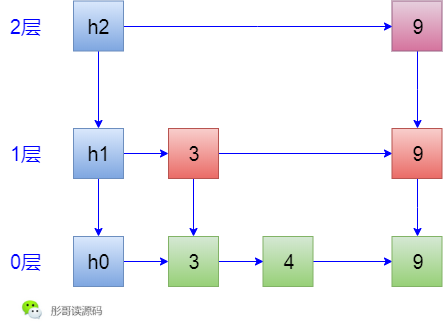
5. 接著,插入了元素1和7,它們都無驚無喜,沒有形成索引:
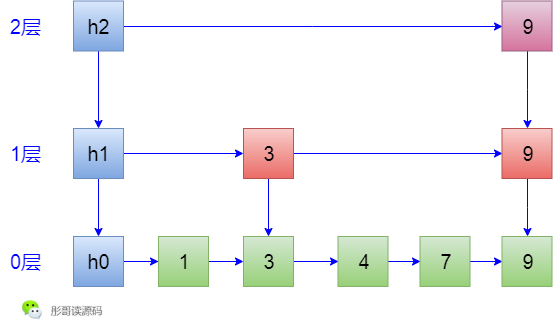
6. 插入元素6,根據索引,查詢路線為,h2->h1->3->3->4,咦,發現4下一個是7了,所以,6放在4和7之間,然後,決定要不要形成索引,隨機決定說我要形成索引,而且我也要形成2層索引,這時候就很麻煩了,在形成6這個元素索引的時候,需要修改3->9這條線,還要修改h2->9這條線,生成的結果如下:
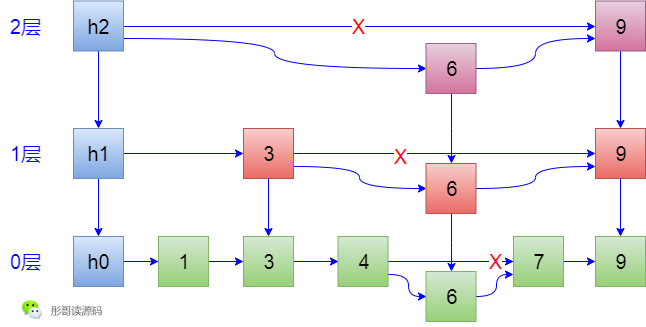
7. 後面,插入了元素8和10,都是無驚無險,沒有產生任何索引,所以,最後的結果如下:
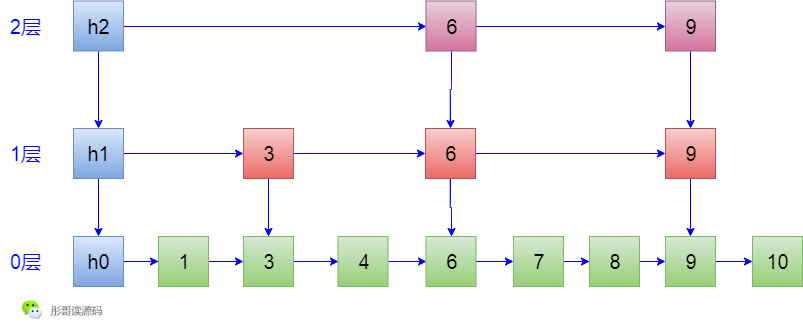
可以看到,跳錶是一個非常隨意的資料結構,即使按照同樣的順序重新插入一遍元素,生成的跳錶也可能完全不一樣,任性,所以,我很喜歡跳錶這種資料結構。
**第四個問題:上面描述了插入元素的過程,刪除過程是怎麼樣的呢?**
刪除過程,首先也要查詢到元素,但是,有一點點小區別,非常小的區別,很難描述,比如,要刪除6這個元素,我能不能從h2->6->6->6這個路徑過來呢?
不能,因為從這條路徑過來,刪除第1層的索引6後,無法修復3->9這條線,所以,刪除元素的時候只能走h2->h1->3->3->4->6這條路徑,且把途中每一層最後經過的索引記住,才能在刪除了6這個元素之後正確地修復各層的索引。
刪除6之後的樣子如下:
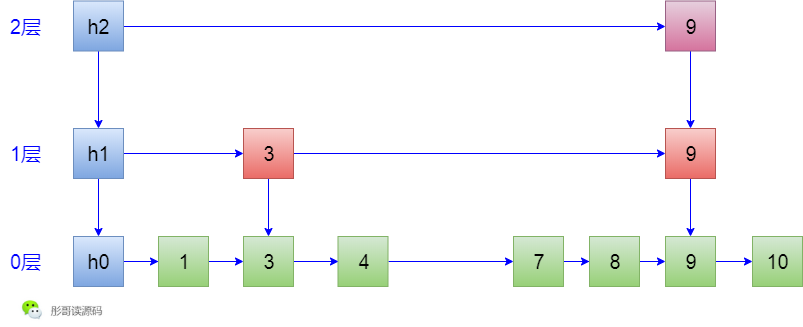
咦,講到這裡,我不經想起了Java跳錶ConcurrentSkipListMap中的一個小優化項,在ConcurrentSkipListMap中,不管是查詢、插入,還是刪除,都是走的跟刪除相同的查詢路徑,其實,可以簡單地優化一下,插入和查詢的時候完全可以走另一條路徑。
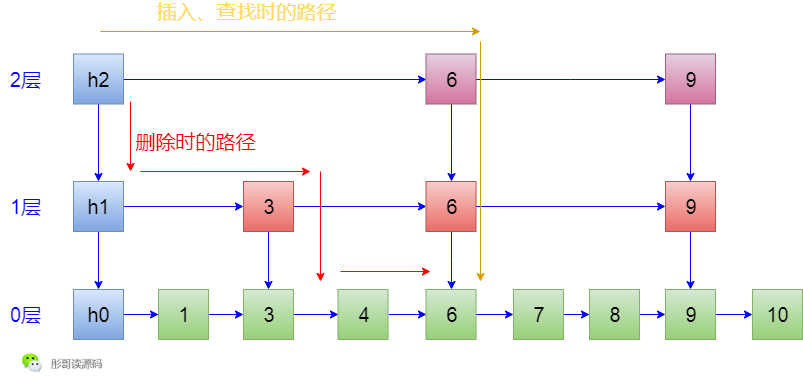
有興趣的同學可以扒一下我的原始碼分析:[死磕 java集合之ConcurrentSkipListMap原始碼分析](https://mp.weixin.qq.com/s/yd2sOhmVtZeEkJ06cTE7qA)
好了,關於跳錶的理論知識我們就講解到這裡。
# 後記
本節,我們通過一步一圖的方式完整清晰地展示了跳錶查詢、插入、刪除元素的全過程,你有沒有Get到呢?能吊打面試官了麼?
然而,很多同學可能會說“Talk is cheap, Show me the code”,OK,下一節,我就將用程式碼的方式給你展現跳錶實現的細節,並使用跳錶改寫HashMap,Next Part 見。
> 關注公主號“彤哥讀原始碼”,解鎖更多原始碼、基礎、架構
