和演算法渣一起練習--利用位運算,輕輕鬆鬆就能解決數學裡的子集問題
阿新 • • 發佈:2020-09-27
# 前言
為什麼要說演算法?老實說,演算法的重要性其實是毋庸置疑的,當然了,平時做CURD工作的時候,其實資料結構其實更重要一些,比如表的設計,以及部分場景下,比如秒殺這類,一般是需要在redis等記憶體中去維護一些資料結構,方便我們提升效能。
但基本來說,部分場景下,定下了資料結構,也就間接地定下了對應的演算法;對於一個數組,要寫一個演算法,支援隨機讀取,就很簡單;對於一個連結串列,要寫一個演算法,支援隨機讀取,那就得遍歷。
個人覺得,演算法和資料結構是一個並重的關係,資料結構的學習還是相對容易的,演算法嘛,就,啊哈,你懂的。
畢業多年來,也曾經嘗試過多次演算法方面的學習,每次都是不了了之,我覺得,有可能是學習的方式不太對。以前看演算法,要麼拿本書在那看;要麼弄不出來,就把答案找出來看一遍,看了就算完了,有時候呢,會把答案的程式碼debug一遍。
總的來說,學習效果真的太差了。
寫這個系列(我也不知道能不能堅持,至少先開一個頭),就是這麼想的,學一個東西,不管是啥,不僅要有輸入,也要有輸出,輸出是什麼呢,就是把我覺得已經會了的東西,講給大家聽,大家能學到一點,我也高興;學不到,那就傾聽並改進。
也鼓勵大家去輸出,不管是筆記,腦圖,還是部落格,都是一個沉澱的方式,大家可以自由選擇。
好了,大家就跟著我這個演算法渣一起,學一點演算法吧。
# 題目描述及解析
原題連結:https://leetcode-cn.com/problems/subsets/
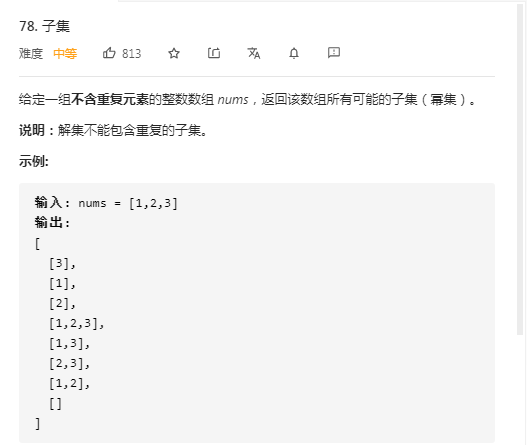
這個題目,大家看上面的示例部分可以知道,就是給你一個整數集合,返回它的全部子集,比如給你一個集合[1,2],那它的子集就有:
```java
[],[1],[2],[1,2]
```
我們再來看看,最終的子集的數量,和集合中元素的個數,似乎有關係,比如,集合[1,2]中包含2個元素,最終結果是4個子集,正好是2的2次方;集合[1,2,3]中包含3個元素,最終結果是8個子集,則是2的3次方。
總結下來就是,集合中有n個元素,則最終子集個數為2的n次方。
這難道是巧合嗎,我覺得不是,大家可以思考下,這個題,像不像是從一堆球中,選擇其中的一部分球。對於每一個球來說,只有兩種結果:被選中或者沒被選中。
針對每個球,有2種選法,那n個球,是不是就是2的n次方種選法呢?
如果用true,false來表達被選中和沒被選中,那麼,針對[1,2,3]這個集合來說,可能的子集,可以如下表示:
```java
1被選中 2被選中 3被選中
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
```
但是,我發現,用程式來生成這樣一個集合,並不容易,具體怎麼不容易,可以自行試試哈。
我們轉換下思路,採用0表示沒被選中,1表示選中。
| 1被選中 | 2被選中 | 3被選中 | 子集 | 二進位制數 | 十進位制數 |
| ------- | ------- | ------- | ------- | -------- | -------- |
| 0 | 0 | 0 | [] | 000 | 0 |
| 0 | 0 | 1 | [3] | 001 | 1 |
| 0 | 1 | 0 | [2] | 010 | 2 |
| 0 | 1 | 1 | [2,3] | 011 | 3 |
| 1 | 0 | 0 | [1] | 100 | 4 |
| 1 | 0 | 1 | [1,3] | 101 | 5 |
| 1 | 1 | 0 | [1,2] | 110 | 6 |
| 1 | 1 | 1 | [1,2,3] | 111 | 7 |
上面的表格中,我們羅列了全部的組合,注意倒數第二列,我們使用二進位制數來表達這個選項,比如001,表示只選中了3.
那麼,我們應該就可以遍歷000到111,就得到了所有的子集,而轉換為十進位制,就是從000遍歷到(2的n次方-1)。
大體的邏輯就是這樣:
```java
int resultLength = 1 << 3; (即2的3次方)
for(int i = 0; i < resultLength; i++){
// 使用java.lang.Integer#toBinaryString,可直觀看到該int對應的二進位制位
System.out.println(Integer.toBinaryString(i));
// todo 根據當前二進位制,來選擇對應的元素
}
```
下邊的程式碼比較直觀:
```java
int resultLength = 1 << 3;
for (int i = 0; i < resultLength; i++) {
System.out.println(Integer.toBinaryString(i));
}
```
輸出如下:
```java
0
1
10
11
100
101
110
111
```
# 通過位運算,來選擇出對應的元素
現在的問題變成了,假設當前遍歷到6,即110這個選項時,我們人類,可以知道該選項對應了[1,2].
但是計算機要怎麼來對應呢?我們可以遍歷我們的陣列,來依次檢查每個元素對應的二進位制bit是否為1,如果為1,說明該元素被選中了,加到結果集中,比如遍歷到1這個元素的時候,它在陣列中的下標為0(陣列下標從0開始別忘)。
那麼,那麼它在110這個二進位制中,它是儲存在哪個bit呢?是儲存在最高位的bit的。 
所以,對於陣列[1,2,3]中的第一個值1,其對應了二進位制中的高位,需要右移n-1(n為陣列長度,這裡為3),即右移2位後進行計算;
對於陣列[1,2,3]中的第二個值2,其對應了二進位制中的第1位,需要右移3-2位,即右移1位。
對於陣列中第三個值3,其對應了二進位制中的第0位,需要右移3-3位,即不需移位。
好了,接下來,我們轉換為程式碼:
```java
class Solution {
public static void main(String[] args) {
List> set = subsets(new int[]{1, 2, 3});
for (List integers : set) {
// System.out.println(integers);
}
}
public List> subsets(int[] nums) {
if (nums == null || nums.length == 0){
List list = new ArrayList();
List> result = new ArrayList>();
result.add(list);
return result;
}
int arraySize = 1 << nums.length;
List> result = new ArrayList>(arraySize);
for (int i = 0; i < arraySize; i++){
// leetcode提交時,記得註釋掉,列印比較費時間
System.out.println(Integer.toBinaryString(i));
// 用來存放當前選項下的結果集
List list = new ArrayList();
// 遍歷陣列
for (int j = 0; j < nums.length; j++){
// 找到要右移的位數; 假設為第一個數,則需要右移2位
int moveStep = nums.length - j - 1;
// 判斷該bit是否為1,為1表示該數被選中
if (((i >
