# 變截距面板資料模型 ## 變截距面板資料模型理論介紹 ### 混合效應模型 #### 背景思想 迴歸公式可以忽略個體與時間變化的差異，因此所有的資料特徵可以通過一個公式進行刻畫。進行資料的大雜燴、亂燉。為什麼採取這麼直接粗暴的方式呢？因為每個品種的菜(個體與時間維度)都很少，每一個品種的菜都不能夠做出完整一盤菜，只能將所有的菜雜七雜八的混合起來亂燉。亂燉雖說精度不高，可是總比沒法處理要好很多。 #### 模型假定 1.$E(\varepsilon_{it})=0$; 2.$var(\varepsilon)=\sigma_\varepsilon為常數$； 3. $\varepsilon_{it}與X_{it}不相關$; #### 公式： $Y_{it}=\alpha + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ 專案 | 含義 -------- | ----- $i$ | 個體標誌序數 $t$ | 時間序數 $X_{it}$ | 觀測變數，$K*1$向量，$(X_{1it,},X_{2it},..,X_{kit})'$ $\beta$ | 引數，$K*1$向量, $(\beta_{1},\beta_{2},..,\beta_{k})'$ $\alpha$ | 截距項 $\varepsilon_{it}$ | 隨機擾動項 #### 估計方法展示 ##### 資料結構展示：  ##### 估計方法： 這個模型是將所有的資料$(y,x_1,x_2,x_3,x_4)$，**直接**匯入公式$Y_{it}=\alpha + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$進行迴歸，只能求出一組$(\beta_{1},\beta_{2},..,\beta_{k})'$，意味著$\beta$在不同個體、不同時點上都是同一組，它不會因為時間或個體而發生變動。 ### 固定效應模型 #### 背景思想 當你擁有蔬菜的品種足夠多，你就可以依據他們的味道單獨做一些小炒菜。有一些影響因素A隨著一些條件的改變而改變，但是這個因素A並未通過$X$觀測變數納入模型，比如說我們研究消費函式，$C = \alpha + \beta Y + \varepsilon$, 這裡的$\alpha$叫做自發消費，這個自發性消費是可能和個人特徵、所處的社會文化、教育等未觀測變數有關，換句話說，截距項 $\alpha$ 和個體某些未觀測到的特質有關，而不和$Y$有關。**$\alpha$和$\varepsilon$都是代表了不可觀測因素的影響，前者的影響因素是有趨勢的(常數也是一種趨勢)，後者的影響因素是無趨勢的。更簡單的理解就是，$\alpha$存在的意義就是為了使$\varepsilon$擁有零均值。** - 當這個截距項與個體特徵相關時，我們稱為個體固定效應模型。 - 當這個截距項與時間特徵有關時，我們稱為時間固定效應模型。 - 同理，和A潛在變數有關，我們就可以稱它為A的固定效應模型。 - 當這個截距項與個體特徵和時間特徵都相關時，我們稱為雙固定效應模型。 - 同理，也可以同時依據三種或三種以上的變數進行分類，迴歸得出它們影響的截距項的估計值。 #### 個體固定效應模型 ##### 模型假設 1.$E(\varepsilon_{it})=0$; 2.$var(\varepsilon)=\sigma_\varepsilon為常數$； 3 $\varepsilon_{it}與X_{it}不相關$; 4. $\alpha_i 與X_{it}相關$ 5. $E(\alpha_i)=0$ ##### 模型公式 $Y_{it}=\alpha_0 +\alpha_i + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ 專案 | 含義 -------- | ----- $i$ | 個體標誌序數 $t$ | 時間序數 $X_{it}$ | 觀測變數，$K*1$向量，$(X_{1it,},X_{2it},..,X_{kit})'$ $\beta$ | 引數，$K*1$向量, $(\beta_{1},\beta_{2},..,\beta_{k})'$ $\alpha_0$ | 常數項 $\alpha_i$ | 個體效應 $\alpha_0+\alpha_i$ | 截距項 $\varepsilon_{it}$ | 隨機擾動項 補充：也寫為 $Y_{it}=u_i+ X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ $u_i = \alpha_0 +\alpha_i, E(u_i)= \alpha_0,E(\alpha_i)=0$ ##### 估計方法展示 資料結構如下：  1.組內（within）估計（離差估計） 離差估計就是剔除常數項，然後進行估計，首先明白我們的目標：分別計算$a,b,c,d,e$組內的截距和各自的組內$\beta$ .其實，不需要離差就可以迴歸。將a,b,c,d,e組的資料分別帶入$Y_{it}=\alpha_0 +\alpha_i + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$，就可以得到結果。 - 離差方差推導 原方程： $Y_{it}=\alpha_0 +\alpha_i + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ 求均值方程： $\bar Y_{i}=\alpha_0 +\alpha_i + \bar X_{i}' \beta + \bar \varepsilon_{i},i = 1,2,3,...,N;t=1,2,3,...,T$ 離差變換（原方程減均值方程）： $Y_{it}-\bar Y_{i}=\alpha_0 +\alpha_i -(\alpha_0 +\alpha_i)+ X_{it}' \beta - \bar X_{i}' \beta+ \varepsilon_{it}-\bar \varepsilon_{i}= X_{it}' \beta - \bar X_{i}' \beta+ \varepsilon_{it}-\bar \varepsilon_{i},i = 1,2,3,...,N;t=1,2,3,...,T$ $\bar Y_i= \frac{1}{T}\displaystyle\sum_{t=1}^T(Y_{it})$ $\bar X_i= \frac{1}{T}\displaystyle\sum_{t=1}^T(X_{it})$ - 帶入離差資料求解,文字描述 通過$(y,x_1,x_2,x_3,x_4)$計算組內時間上的均值$\bar{(y,x_1,x_2,x_3,x_4)}$，然後計算離差$(y,x_1,x_2,x_3,x_4)- \bar{(y,x_1,x_2,x_3,x_4)}$,帶入離差方程$Y_{it}-\bar Y_{i}= X_{it}' \beta - \bar X_{i}' \beta+ \varepsilon_{it}-\bar \varepsilon_{i},i = 1,2,3,...,N;t=1,2,3,...,T$進行估計。 - 利用估計出的$\beta$帶入均值方程$\bar Y_{i}=\alpha_0 +\alpha_i + \bar X_{i}' \beta + \bar \varepsilon_{i},i = 1,2,3,...,N;t=1,2,3,...,T$，求解組內的($\alpha_0 +\alpha_i$) - 通過上一步$N$個組的($\alpha_0 +\alpha_i$)，求解$\alpha_0 = \frac{1}{N}\displaystyle\sum_{t=1}^N(\alpha_0 +\alpha_i)$,依據假設5：$E(\alpha_i)=0$ - 再求解$\alpha_i = (\alpha_0 +\alpha_i) - \alpha_0$ 2.一階差分估計 **原理：** 因為$\alpha_0 +\alpha_i$是不受時間影響的，所以我們可以使用差分方法消去常數項 - 差分方程推導 原方程： $Y_{it}=\alpha_0 +\alpha_i + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ 上一期方程： $Y_{i,t-1}=\alpha_0 +\alpha_i + X_{i,t-1}' \beta + \varepsilon_{i,t-1},i = 1,2,3,...,N;t=1,2,3,...,T$ 原方程減上一期方程： $Y_{it}-Y_{i,t-1}=\alpha_0 +\alpha_i + X_{it}' \beta + \varepsilon_{it}-\alpha_0 - \alpha_i - X_{i,t-1}' \beta - \varepsilon_{i.t-1} = X_{it}' \beta -X_{i,t-1}' \beta + \varepsilon_{it}- \varepsilon_{i,t-1}$ - 資料代入求解即可。 - 此方法無法求解截距項。 3.LSDV(最小二乘虛擬變數法) 學過計量的小夥伴們應該熟悉虛擬變數法，將個體差異以截距項形式的虛擬變數加入。 估計方程形式： $Y = D \alpha+X\beta + \varepsilon$ $D=\begin{pmatrix} D_1 & D_2&D_3&...&D_N \end{pmatrix}$ 其中： $D_N=\begin{cases} 1 &\text{if } 為N組 \\ 0 &\text{if } 不為N組 \end{cases}$ #### 時點固定效應模型 ##### 模型假設 1.$E(\varepsilon_{it})=0$; 2.$var(\varepsilon)=\sigma_\varepsilon為常數$ 3 $\varepsilon_{it}與X_{it}不相關$; 4. $\lambda_i 與X_{it}相關$； ##### 模型公式 $Y_{it}=\lambda_0 +\lambda_i + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ 專案 | 含義 -------- | ----- $i$ | 個體標誌序數 $t$ | 時間序數 $X_{it}$ | 觀測變數，$K*1$向量，$(X_{1it,},X_{2it},..,X_{kit})'$ $\beta$ | 引數，$K*1$向量, $(\beta_{1},\beta_{2},..,\beta_{k})'$ $\lambda_0$ | 常數項 $\lambda_i$ | 時間效應 $\lambda_0+\lambda_i$ | 截距項 $\varepsilon_{it}$ | 隨機擾動項 ##### 估計方法展示 資料結構如下：  LSDV(最小二乘虛擬變數法) 學過計量的小夥伴們應該熟悉虛擬變數法，將時間段以截距項形式的虛擬變數加入。 估計方程形式： $Y = D\lambda+X\beta + \varepsilon$ $D=\begin{pmatrix} D_1 & D_2&D_3&...&D_T \end{pmatrix}$ 其中： $D_T=\begin{cases} 1 &\text{if } 為T時期 \\ 0 &\text{if } 不為T時期 \end{cases}$ #### 個體時點固定效應模型 ##### 模型假設 1 $E(\varepsilon_{it})=0$; 2 $var(\varepsilon)=\sigma_\varepsilon為常數$ 3 $\varepsilon_{it}與X_{it}不相關$; 4 $\lambda_i 與X_{it}相關$； 5 $\alpha_i 與X_{it}相關$； 6 $E(\alpha_i)=0$； 7 $E(\lambda_i)=0$； 這裡我們設定： $\tilde{\alpha}_i=\alpha_0+\alpha_i;\tilde{\lambda}_i=\lambda_0+\lambda_i$; 8 $E(\tilde{\alpha}_i)=\alpha_0$; 9 $E(\tilde{\lambda}_i)=\lambda_0$; ##### 模型公式 $Y_{it}=(\alpha_0 +\lambda_0)+\alpha_i +\lambda_i + X_{it}' \beta + \varepsilon_{it}$ $=\alpha_0 +\alpha_i + \lambda_0 +\lambda_i + X_{it}' \beta + \varepsilon_{it}$ $=\tilde{\alpha}_i+\tilde{\lambda}_i+X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ 專案 | 含義 -------- | ----- $i$ | 個體標誌序數 $t$ | 時間序數 $X_{it}$ | 觀測變數，$K*1$向量，$(X_{1it,},X_{2it},..,X_{kit})'$ $\beta$ | 引數，$K*1$向量, $(\beta_{1},\beta_{2},..,\beta_{k})'$ $\lambda_0$ | 時間效應的常數項 $\lambda_i$ | 時間效應 $\alpha_0$ | 個體特徵的常數項 $\alpha_i$ | 個體效應 $\alpha_0+\alpha_i+\lambda_0+\lambda_i$ | 截距項 $\varepsilon_{it}$ | 隨機擾動項 ##### 估計方法 資料結構展示：  LSDV(最小二乘虛擬變數法) 學過計量的小夥伴們應該熟悉虛擬變數法，將時間段以截距項形式的虛擬變數加入。 - 估計方程形式： $Y = D_{\lambda}\lambda + D_\alpha\alpha+X\beta + \varepsilon$ $D_{\lambda}=\begin{pmatrix} D_1 & D_2&D_3&...&D_T \end{pmatrix}$ 其中： $D_T=\begin{cases} 1 &\text{if } 為T時期 \\ 0 &\text{if } 不為T時期 \end{cases}$ $D_\alpha=\begin{pmatrix} D_1 & D_2&D_3&...&D_N \end{pmatrix}$ 其中： $D_N=\begin{cases} 1 &\text{if } 為N組 \\ 0 &\text{if } 不為N組 \end{cases}$ - 也可以將時間與個體效應混合 $Y = Dh + X\beta + \varepsilon$ $D=\begin{pmatrix} D_1 & D_2&D_3&...&D_{N*T} \end{pmatrix}$ 其中： $D=\begin{cases} 1 &\text{if } 為第N個體的T時期 \\ 0 &\text{if } 不為第N個體的T時期 \end{cases}$ #### 個體時點雙固定效應，控制區域、行業等模型 ##### 模型假設 1 $E(\varepsilon_{it})=0$; 2 $var(\varepsilon)=\sigma_\varepsilon為常數$ 3 $\varepsilon_{it}與X_{it}不相關$; 4 $\lambda_i 與X_{it}相關$； 5 $\alpha_i 與X_{it}相關$； 6 $E(\alpha_i)=0$； 7 $E(\lambda_i)=0$； 這裡我們設定： $\tilde{\alpha}_i=\alpha_0+\alpha_i;\tilde{\lambda}_i=\lambda_0+\lambda_i$; 8 $E(\tilde{\alpha}_i)=\alpha_0$; 9 $E(\tilde{\lambda}_i)=\lambda_0$; ##### 模型公式 $Y_{it}=\tilde{\alpha}_i+\tilde{\lambda}_i+D_{type}\gamma+X_{it}' \beta + \varepsilon_{it}, i = 1,2,3,...,N;t=1,2,3,...,T$ *這個方程為了方便理解而設定，其中$\tilde{\alpha}_i與D_{type}$存在共線性問題，畢竟型別屬性也是個體特徵的一部分嘛！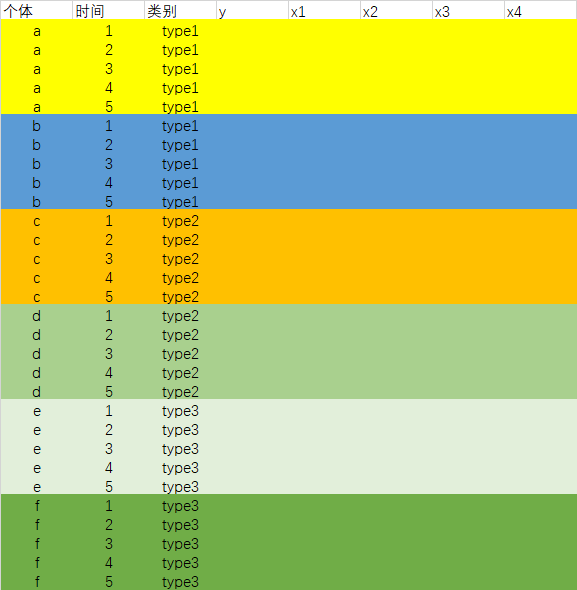* 專案 | 含義 -------- | ----- $i$ | 個體標誌序數 $t$ | 時間序數 $X_{it}$ | 觀測變數，$K*1$向量，$(X_{1it,},X_{2it},..,X_{kit})'$ $\beta$ | 引數，$K*1$向量, $(\beta_{1},\beta_{2},..,\beta_{k})'$ $\lambda_0$ | 時間效應的常數項 $\lambda_i$ | 時間效應 $\alpha_0$ | 個體特徵的常數項 $\alpha_i$ | 個體效應 $\alpha_0+\alpha_i+\lambda_0+\lambda_i$ | 截距項 $\varepsilon_{it}$ | 隨機擾動項 $D_{type}$ | 型別的虛擬變數 ##### 估計方法展示 資料展示  估計方法：同上，將型別變數按照虛擬變數加入方程即可。 ### 隨機效應模型 背景思想：每組估計值的截距項的變動不與X的特徵有關。 #### 個體隨機效應 ##### 模型假設 1.$E(\varepsilon_{it})=0$; 2.$var(\sigma_\varepsilon)為常數$； 3 $\varepsilon_{it}與X_{it}不相關$; 4. $\alpha_i 與X_{it},\varepsilon_{it}不相關$; 5. $\alpha_i \thicksim i.i.d(0,\sigma_\alpha^2)$; ##### 公式： $Y_{it}=\alpha_0 +\alpha_i + X_{it}' \beta + \varepsilon_{it},i = 1,2,3,...,N;t=1,2,3,...,T$ $=\alpha_0 + X_{it}' \beta +(\alpha_i+ \varepsilon_{it}),i = 1,2,3,...,N;t=1,2,3,...,T$ $=\alpha_0 + X_{it}' \beta + v_{it}, v_{it}=\alpha_i + \varepsilon_{it}, i = 1,2,3,...,N;t=1,2,3,...,T$ 專案 | 含義 -------- | ----- $i$ | 個體標誌序數 $t$ | 時間序數 $X_{it}$ | 觀測變數，$K*1$向量，$(X_{1it,},X_{2it},..,X_{kit})'$ $\beta$ | 引數，$K*1$向量, $(\beta_{1},\beta_{2},..,\beta_{k})'$ $\alpha_0$ | 常數項 $\alpha_i$ | 隨機效應 $\alpha_0+\alpha_i$ | 截距項 $\varepsilon_{it}$ | 隨機擾動項 $v_{it}=\alpha_i + \varepsilon_{it}$ | 新的隨機擾動項 根據$v_{it}=\alpha_i + \varepsilon_{it}$；$\alpha_i \thicksim i.i.d(0,\sigma_\alpha^2)$;$\alpha_i 與X_{it},\varepsilon_{it}不相關$;$var(\varepsilon)=\sigma_\varepsilon為常數$ 推導： $cov(v_{it},v_{is})=cov(\alpha_i + \varepsilon_{it},\alpha_i + \varepsilon_{is})=cov(\alpha_i ,\alpha_i + \varepsilon_{is})+cov(\varepsilon_{it},\alpha_i + \varepsilon_{is})=cov(\alpha_i ,\alpha_i )+cov(\alpha_i ,\varepsilon_{is})+cov(\varepsilon_{it},\alpha_i )+ cov(\varepsilon_{it},\ \varepsilon_{is}) =\begin{cases} \sigma_\alpha^2 &\text{if } t \neq s \\ \sigma_\alpha^2 + \sigma_\varepsilon &\text{if } t=s \end{cases}$ 所以不滿足古典假定，存在異方差與自相關問題。 ##### 估計方法展示 - 可行的廣義最小二乘法(FGLS) ## 模型設定檢驗 ### F檢驗（chow's test） 原假設：混合迴歸模型 備擇假設：其他模型 以個體固定效應模型為例：$Y_{it}=u_i+X_{it}'\beta+ \varepsilon_{it}$ 原假設：$u_1=u_2=...=u_N$ （存在約束，截距不會變） $Y_{it}=u_i+X_{it}'\beta+ \varepsilon_{it}$ 計算迴歸的$RSS_r$ 備擇假設：$u_1，u_2，...，u_N不全相等$ （無約束，截距會變） $Y_{it}=u_i+X_{it}'\beta+ \varepsilon_{it}$ 計算迴歸的$RSS_u$ F統計量構造： $F=\cfrac{(RSS_r-RSS_u)/[(NT-k-1)-(NT-k-N)]}{RSS_u/(NT-k-N)} \thicksim F(N-1,NT-k-N)$ 專案 | 含義 -------- | ----- $RSS_r$ | 有約束模型的殘差平方和(混合模型，有約束) $RSS_u$ | 無約束模型的殘差平方和(變截距模型) $k$ | 解釋變數個數 ### LR檢驗 原假設：混合迴歸模型 備擇假設：其他模型 以個體固定效應模型為例：$Y_{it}=u_i+X_{it}'\beta+ \varepsilon_{it}$ 原假設：$u_1=u_2=...=u_N$ （存在約束，截距不會變） $Y_{it}=u_i+X_{it}'\beta+ \varepsilon_{it}$ 計算迴歸的最大似然函式值的對數$ln(L_r)$ 備擇假設：$u_1，u_2，...，u_N不全相等$ （無約束，截距會變） $Y_{it}=u_i+X_{it}'\beta+ \varepsilon_{it}$ 計算迴歸的最大似然函式值的對數$ln(L_u)$ LR統計量構造： $LR=-2(lnL_r-lnL_u)漸近服從\chi^2(約束條件的個數: N-1)$ ### 豪斯曼檢驗（Hauseman's test） 原假設：個體隨機效應模型(個體效應與迴歸變數無關) 備擇假設：個體固定效應模型(個體效應與迴歸變數有關) 檢驗的原理： 利用組內估計(within)，無論是隨機效應模型的引數估計值還是固定效應模型的引數估計值，估計引數值都是一致的 利用廣義最小二乘法，對隨機效應模型的引數估計值是一致的，對於隨機效應模型的引數估計值是不一致的 真實模型 | 組內估計$\hat\beta_w$ | 廣義最小二乘法$\tilde{\beta_{re}}$ -------- | ----- |---- $隨機效應模型$ | 一致估計量 | 非一致估計量 $固定效應模型$ | 一致估計量 | 一致估計量 ### 檢驗邏輯圖： ```mermaid graph LR A[F檢驗 or LR檢驗] --不拒絕原假設,意味著截距項不變動--> B[使用混合迴歸] A --拒絕原假設,意味著截距項變動--> C[豪斯曼檢驗] C --不拒絕原假設--> D[選擇個體隨機效應模型] C --拒絕原假設--> E[選擇個體固定效應模型] ``` ## 變截距面板資料模型建模步驟 ```mermaid graph LR A[輸入資料]-->B[描述性統計分析]-->C[面板單位根檢驗] C--資料非平穩-->D[面板協整分析] C--資料平穩-->E[變截距檢驗] & F[變係數檢驗] E[F檢驗 or LR檢驗] --不拒絕原假設,意味著截距項不變動--> G[使用混合迴歸] E --拒絕原假設,意味著截距項變動--> H[豪斯曼檢驗] H --不拒絕原假設--> L[選擇個體隨機效應模型] H --拒絕原假設--> M[選擇個體固定效應模