五大常用演算法:一文搞懂分治演算法
阿新 • • 發佈:2020-12-03
>原創公眾號:bigsai
>文章收錄在 [bigsai-algorithm](https://github.com/javasmall/bigsai-algorithm)
## 前言
分治演算法(divide and conquer)是五大常用演算法(分治演算法、動態規劃演算法、貪心演算法、回溯法、分治界限法)之一,很多人在平時學習中可能只是知道分治演算法,但是可能並沒有系統的學習分治演算法,本篇就帶你較為全面的去認識和了解分治演算法。
在學習分治演算法之前,問你一個問題,相信大家小時候都有存錢罐的經歷,父母親人如果給錢都會往自己的寶藏中存錢,我們每隔一段時間都會清點清點錢。但是一堆錢讓你處理起來你可能覺得很複雜,因為資料相對於大腦有點龐大了,並且很容易算錯,你可能會將它**先分**成幾個小份算,然後**再疊加**起來計算總和就獲得這堆錢的總數了
當然如果你覺得各個部分錢數量還是太大,你依然可以進行劃分然後合併,我們之所以這麼多是因為:
- 計算每個小堆錢的方式和計算最大堆錢的方式是相同的(區別在於體量上)
- 然後大堆錢總和其實就是小堆錢結果之和。這樣其實就有一種分治的思想。
當然這些錢都是想出來的……

## 分治演算法介紹
**分治演算法是用了分治思想的一種演算法,什麼是分治**?
分治,字面上的解釋是“**分而治之**”,就是把一個複雜的問題分成兩個或更多的相同或相似的子問題,再把子問題分成更小的子問題……直到最後子問題可以簡單的直接求解,原問題的解即子問題的解的合併。在電腦科學中,分治法就是運用分治思想的一種很重要的演算法。分治法是很多高效演算法的基礎,如排序演算法(快速排序,歸併排序),傅立葉變換(快速傅立葉變換)等等。
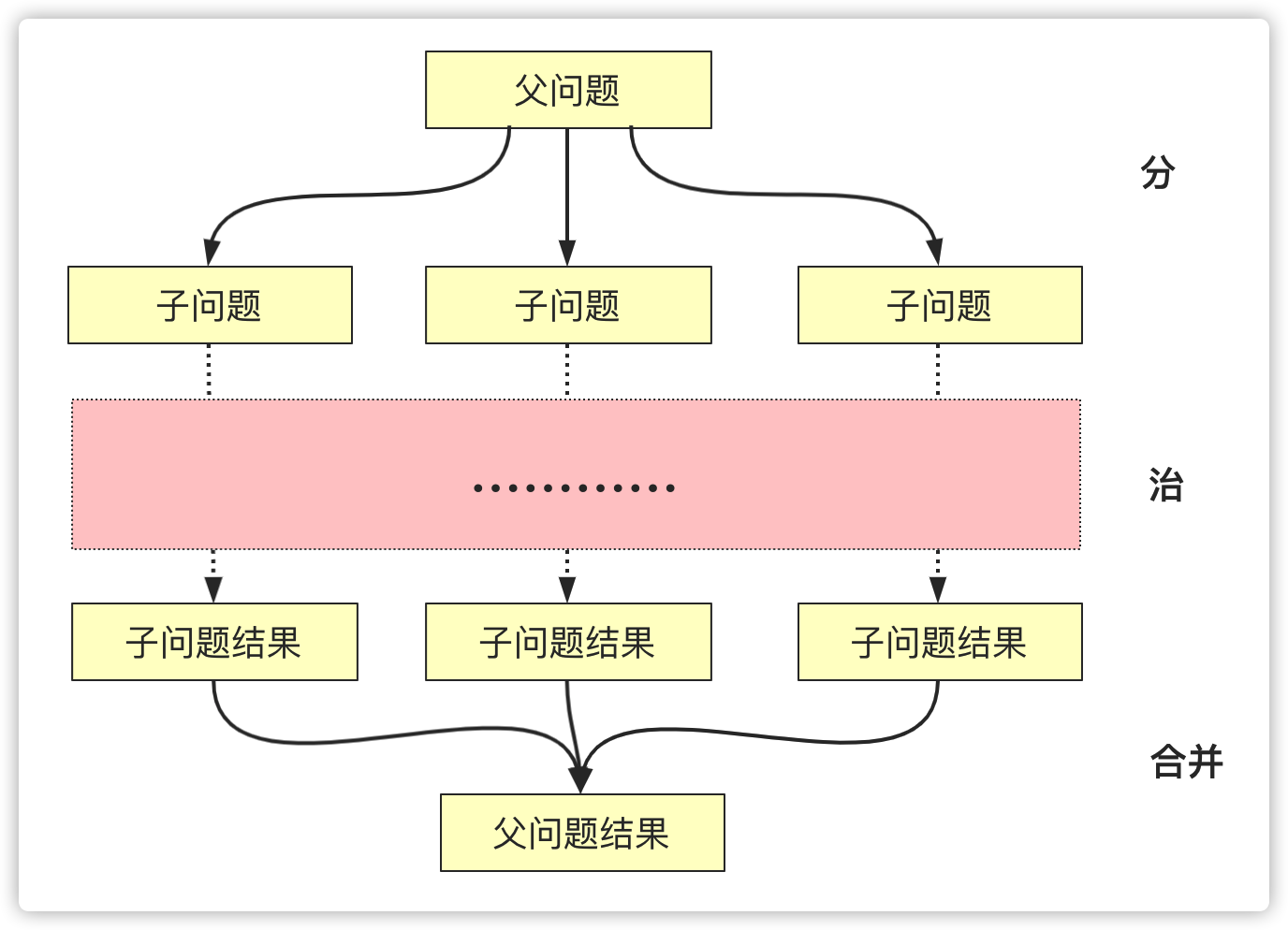
將父問題分解為子問題同等方式求解,這和遞迴的概念很吻合,所以在分治演算法通常以遞迴的方式實現(當然也有非遞迴的實現方式)。分治演算法的描述從字面上也很容易理解,分、治其實還有個合併的過程:
- 分(Divide):遞迴解決較小的問題(到終止層或者可以解決的時候停下)
- 治(Conquer):遞迴求解,如果問題夠小直接求解。
- 合併(Combine):將子問題的解構建父類問題
一般分治演算法在正文中分解為兩個即以上的遞迴呼叫,並且子類問題一般是不想交的(互不影響)。當求解一個問題規模很大很難直接求解,但是規模較小的時候問題很容易求解並且這個問題並且問題滿足分治演算法的適用條件,那麼就可以使用分治演算法。
那麼採用分治演算法解決的問題需要 **滿足那些條件(特徵)** 呢?
1 . 原問題規模通常比較大,不易直接解決,但問題縮小到一定程度就能較容易的解決。
2 . 問題可以分解為若干規模較小、求解方式相同(似)的子問題。且子問題之間求解是獨立的互不影響。
3 . 合併問題分解的子問題可以得到問題的解。
你可能會疑惑分治演算法和遞迴有什麼關係?其實分治重要的是一種思想,注重的是問題分、治、合併的過程。而遞迴是一種方式(工具),這種方式通過方法自己呼叫自己形成一個來回的過程,而分治可能就是利用了多次這樣的來回過程。
## 分治演算法經典問題
對於分治演算法的經典問題,重要的是其思想,因為我們大部分藉助遞迴去實現,所以在程式碼實現上大部分都是很簡單,而本篇也重在講述思想。
分治演算法的經典問題,個人將它分成兩大類:子問題完全獨立和子問題不完全獨立。
1 . 子問題完全獨立就是原問題的答案可完全由子問題的結果推出。
2 . 子問題不完全獨立,有些區間類的問題或者跨區間問題使用分治可能結果跨區間,在考慮問題的時候需要仔細借鑑下。
### 二分搜尋
二分搜尋是分治的一個例項,只不過二分搜尋有著自己的特殊性
- 序列有序
- 結果為一個值
正常二分將一個完整的區間分成兩個區間,兩個區間本應單獨找值然後確認結果,但是通過有序的區間可以直接確定結果在那個區間,所以分的兩個區間只需要計算其中一個區間,然後繼續進行一直到結束。實現方式有遞迴和非遞迴,但是非遞迴用的更多一些:
```java
public int searchInsert(int[] nums, int target) {
if(nums[0]>=target)return 0;//剪枝
if(nums[nums.length-1]==target)return nums.length-1;//剪枝
if(nums[nums.l
