孿生網路入門(下) Siamese Net分類服裝MNIST資料集(pytorch)
阿新 • • 發佈:2020-12-07
---
# 主題列表:juejin, github, smartblue, cyanosis, channing-cyan, fancy, hydrogen, condensed-night-purple, greenwillow, v-green, vue-pro, healer-readable
# 貢獻主題:https://github.com/xitu/juejin-markdown-themes
theme: smartblue
highlight:
---
在上一篇文章中已經講解了Siamese Net的原理,和這種網路架構的關鍵——損失函式contrastive loss。現在我們來用pytorch來做一個簡單的案例。經過這個案例,我個人的收穫有到了以下的幾點:
- Siamese Net適合小資料集;
- 目前Siamese Net用在分類任務(如果有朋友知道如何用在分割或者其他任務可以私信我,WX:cyx645016617)
- Siamese Net的可解釋性較好。
## 1 準備資料
```python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset,DataLoader
from sklearn.model_selection import train_test_split
device = 'cuda' if torch.cuda.is_available() else 'cpu'
```
```python
data_train = pd.read_csv('../input/fashion-mnist_train.csv')
data_train.head()
```
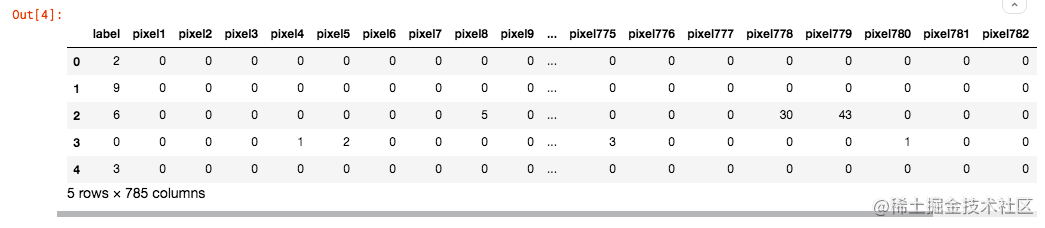
這個資料檔案是csv格式,第一列是類別,之後的784列其實好似28x28的畫素值。
**劃分訓練集和驗證集,然後把資料轉換成28x28的圖片**
```python
X_full = data_train.iloc[:,1:]
y_full = data_train.iloc[:,:1]
x_train, x_test, y_train, y_test = train_test_split(X_full, y_full, test_size = 0.05)
x_train = x_train.values.reshape(-1, 28, 28, 1).astype('float32') / 255.
x_test = x_test.values.reshape(-1, 28, 28, 1).astype('float32') / 255.
y_train.label.unique()
>>> array([8, 9, 7, 6, 4, 2, 3, 1, 5, 0])
```
可以看到這個Fashion MNIST資料集中也是跟MNIST類似,劃分了10個不同的類別。
- 0 T-shirt/top
- 1 Trouser
- 2 Pullover
- 3 Dress
- 4 Coat
- 5 Sandal
- 6 Shirt
- 7 Sneaker
- 8 Bag
- 9 Ankle boot
```python
np.bincount(y_train.label.values),np.bincount(y_test.label.values)
>>> (array([4230, 4195, 4135, 4218, 4174, 4172, 4193, 4250, 4238, 4195]),
array([1770, 1805, 1865, 1782, 1826, 1828, 1807, 1750, 1762, 1805]))
```
可以看到,每個類別的資料還是非常均衡的。
## 2 構建Dataset和視覺化
```python
class mydataset(Dataset):
def __init__(self,x_data,y_data):
self.x_data = x_data
self.y_data = y_data.label.values
def __len__(self):
return len(self.x_data)
def __getitem__(self,idx):
img1 = self.x_data[idx]
y1 = self.y_data[idx]
if np.random.rand() < 0.5:
idx2 = np.random.choice(np.arange(len(self.y_data))[self.y_data==y1],1)
else:
idx2 = np.random.choice(np.arange(len(self.y_data))[self.y_data!=y1],1)
img2 = self.x_data[idx2[0]]
y2 = self.y_data[idx2[0]]
label = 0 if y1==y2 else 1
return img1,img2,label
```
關於torch.utils.data.Dataset的構建結構,我就不再贅述了,在之前的《小白學PyTorch》系列中已經講解的很清楚啦。上面的邏輯就是,給定一個idx,然後我們先判斷,這個資料是找兩個同類別的圖片還是兩個不同類別的圖片。50%的概率選擇兩個同類別的圖片,然後最後輸出的時候,輸出這兩個圖片,然後再輸出一個label,這個label為0的時候表示兩個圖片的類別是相同的,1表示兩個圖片的類別是不同的。這樣就可以進行模型訓練和損失函式的計算了。
```python
train_dataset = mydataset(x_train,y_train)
train_dataloader = DataLoader(dataset = train_dataset,batch_size=8)
val_dataset = mydataset(x_test,y_test)
val_dataloader = DataLoader(dataset = val_dataset,batch_size=8)
```
```python
for idx,(img1,img2,target) in enumerate(train_dataloader):
fig, axs = plt.subplots(2, img1.shape[0], figsize = (12, 6))
for idx,(ax1,ax2) in enumerate(axs.T):
ax1.imshow(img1[idx,:,:,0].numpy(),cmap='gray')
ax1.set_title('image A')
ax2.imshow(img2[idx,:,:,0].numpy(),cmap='gray')
ax2.set_title('{}'.format('same' if target[idx]==0 else 'different'))
break
```
這一段的程式碼就是對一個batch的資料進行一個視覺化:

到目前位置應該沒有什麼問題把,有問題可以聯絡我討論交流,WX:cyx645016617.我個人認為從交流中可以快速解決問題和進步。
## 3 構建模型
```python
class siamese(nn.Module):
def __init__(self,z_dimensions=2):
super(siamese,self).__init__()
self.feature_net = nn.Sequential(
nn.Conv2d(1,4,kernel_size=3,padding=1,stride=1),
nn.ReLU(inplace=True),
nn.BatchNorm2d(4),
nn.Conv2d(4,4,kernel_size=3,padding=1,stride=1),
nn.ReLU(inplace=True),
nn.BatchNorm2d(4),
nn.MaxPool2d(2),
nn.Conv2d(4,8,kernel_size=3,padding=1,stride=1),
nn.ReLU(inplace=True),
nn.BatchNorm2d(8),
nn.Conv2d(8,8,kernel_size=3,padding=1,stride=1),
nn.ReLU(inplace=True),
nn.BatchNorm2d(8),
nn.MaxPool2d(2),
nn.Conv2d(8,1,kernel_size=3,padding=1,stride=1),
nn.ReLU(inplace=True)
)
self.linear = nn.Linear(49,z_dimensions)
def forward(self,x):
x = self.feature_net(x)
x = x.view(x.shape[0],-1)
x = self.linear(x)
return x
```
一個非常簡單的卷積網路,輸出的向量的維度就是z-dimensions的大小。
```python
def contrastive_loss(pred1,pred2,target):
MARGIN = 2
euclidean_dis = F.pairwise_distance(pred1,pred2)
target = target.view(-1)
loss = (1-target)*torch.pow(euclidean_dis,2) + target * torch.pow(torch.clamp(MARGIN-euclidean_dis,min=0),2)
return loss
```
然後構建了一個contrastive loss的損失函式計算。
## 4 訓練
```python
model = siamese(z_dimensions=8).to(device)
# model.load_state_dict(torch.load('../working/saimese.pth'))
optimizor = torch.optim.Adam(model.parameters(),lr=0.001)
```
```python
for e in range(10):
history = []
for idx,(img1,img2,target) in enumerate(train_dataloader):
img1 = img1.to(device)
img2 = img2.to(device)
target = target.to(device)
pred1 = model(img1)
pred2 = model(img2)
loss = contrastive_loss(pred1,pred2,target)
optimizor.zero_grad()
loss.backward()
optimizor.step()
loss = loss.detach().cpu().numpy()
history.append(loss)
train_loss = np.mean(history)
history = []
with torch.no_grad():
for idx,(img1,img2,target) in enumerate(val_dataloader):
img1 = img1.to(device)
img2 = img2.to(device)
target = target.to(device)
pred1 = model(img1)
pred2 = model(img2)
loss = contrastive_loss(pred1,pred2,target)
loss = loss.detach().cpu().numpy()
history.append(loss)
val_loss = np.mean(history)
print(f'train_loss:{train_loss},val_loss:{val_loss}')
```
這裡為了加快訓練,我把batch-size增加到了128個,其他的並沒有改變:
這是執行的10個epoch的結果,不要忘記把模型儲存一下:
```python
torch.save(model.state_dict(),'saimese.pth')
```
差不多是這個樣子,然後看一看驗證集的視覺化效果,這裡使用的是t-sne高位特徵視覺化的方法,其核心是PCA降維:
```python
from sklearn import manifold
'''X是特徵,不包含target;X_tsne是已經降維之後的特徵'''
tsne = manifold.TSNE(n_components=2, init='pca', random_state=501)
X_tsne = tsne.fit_transform(X)
print("Org data dimension is {}. \
Embedded data dimension is {}".format(X.shape[-1], X_tsne.shape[-1]))
x_min, x_max = X_tsne.min(0), X_tsne.max(0)
X_norm = (X_tsne - x_min) / (x_max - x_min) # 歸一化
plt.figure(figsize=(8, 8))
for i in range(10):
plt.scatter(X_norm[y==i][:,0],X_norm[y==i][:,1],alpha=0.3,label=f'{i}')
plt.legend()
```
輸入影象為:
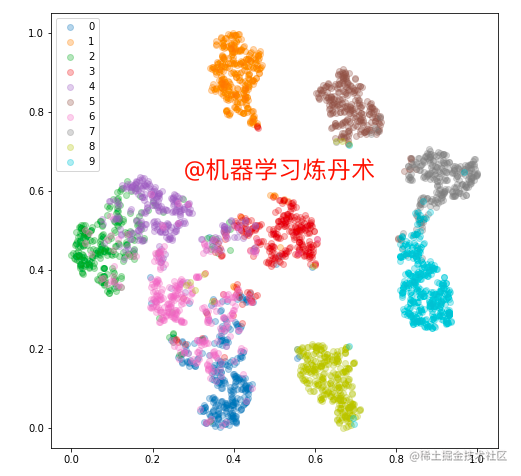
可以看得出來,不同類別之間劃分的是比較好的,可以看到不同類別之間的距離還是比較大的,比較明顯的,**甚至可以放下公眾號的名字**。這裡使用的隱變數是8。
這裡有一個問題,我內心已有答案不知大家的想法如何,**假如我把z潛變數的維度直接改成2,這樣就不需要使用tsne和pca的方法來降低維度就可以直接視覺化,但是這樣的話視覺化的效果並不比從8降維到2來視覺化的效果好,這是為什麼呢?**
提示:一方面在於維度過小導致資訊的缺失,但是這個解釋站不住腳,因為PCA其實等價於一個退化的線形層,所以PCA同樣會造成這種缺失;我認為關鍵應該是損失函式中的歐式距離的計算,如果維度高,那麼歐式距離就會偏大,這樣需要相應的調整MARGIN的
