我們知道機器學習的特點就是：以計算機為工具和平臺，以資料為研究物件，以學習為中心；是概率論，線性代數，數值計算，資訊理論，最優化理論和電腦科學等多個領域的交叉學科。所以這裡我打算補充一下機器學習涉及到的一些常用的知識點。

　　（注意：目前自己補充到的所有知識點，均按照自己網課視訊中老師課程知識點走的，同時一些公式是網友辛辛苦苦敲的，文中用到那個部落格均在文末補充連結地址，這裡首先表示感謝！！）

1，函式

1.1  函式的定義

　　函式（function）的定義通常分為傳統定義和近代定義，函式的兩個定義本質是相同的，只是敘述概念的出發點不同，傳統定義是從運動變換的觀點出發。函式的近代定義是給定一個數據集A，假設其中的元素為x，對A中的元素施加對應法則 f ，記做 f(x)，得到另一資料集B，假設B中的元素為y，則 x 和 y 之間的等量關係可以用 y = f(x) 表示。函式概念含有三個要素：定義域A，值域B和對應法則 f 。其中核心為對應法則 f，它是函式關係的本質特徵。

　　在一個變換過程中，發生變化的量叫變數（數學中，變數為 x ，而 y 則隨 x 值的變化而變化），有些數值是不隨變數而改變的，我們稱他們為常量。

　　自變數（函式）：一個與它量有關係的變數，這一量中的任何一值都能在它量中找到對應的固定值。

　　因變數（函式）：隨著自變數的變化而變化，且自變數取唯一值時，因變數（函式）有且只有唯一值與其對應。

　　函式值：在 y 是 x 的函式中，x 確定一個值，y 就隨之確定一個值，當 x 取 a 時， y 就 隨之確定為 b，b 就叫做 a 的函式值。

　　注意：符號只是一種表示，任何符號都是幫助我們理解的，它本身沒有特殊的含義。都是我們給予賦值操作，也可以如下：

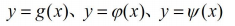
1.2  常見的幾種函式

　　分段函式：就是對於自變數x 的不同取值範圍，有著不同的解析式的函式。它是一個函式，而不是幾個函式；分段函式的定義域是各段函式定義域的並集，值域也是各段函式值域的並集。

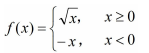
　　反函式：一般來說，設函式 y = f(x) 的值域為C，若是找得到一個函式 g(y) 在每一處 g(y) 都等於 x，這樣的函式 x = g(y) 叫做函式 y = f(x) 的反函式，記做 x = f^-1(y)。反函式 x = f^-1(y) 的定義域，值域分別為函式 y = f(x) 的值域，定義域。最具代表性的反函式就是對數函式與指數函式。

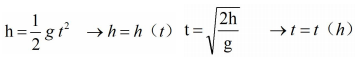
　　顯函式與隱函式：顯函式是函式的型別之一，解析式中明顯的用一個變數的代數式表示另一個變數時，稱為顯函式；如果方程F(x, y) =0 能確定 y 是 x 的函式，那麼稱這種方式表示的函式是隱函式。

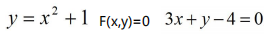
　　狄利克雷函式：是一個定義在實數範圍內，值域不連續的函式。狄利克雷函式的影象以Y軸為對稱軸，是一個偶函式，它處處不連續，處處極限不存在，不可黎曼積分。這是一個處處不連續的可測函式。

　　實數域上的狄利克雷（Dirichlet）函式表示為：

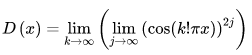
　　其中：k,j 為整數。

　　也可以簡單的表示為分段函式的形式，如下：

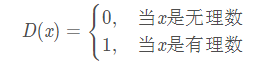
　　狄利克雷函式的性質：

• 1，定義域為整個實數域R，值域為{0, 1}，函式為偶函式
• 2，無法畫出函數週期，但是它的函式影象客觀存在
• 3，以任意正有理數為其週期，無最小正週期（由實數的連續統理論可知其無最小正週期）
• 4，處處不連續，處處不可導，在任何區間內黎曼不可積
• 5，函式是可測函式
• 6，函式是周期函式，但是卻沒有最小正週期，它的週期是任意負有理數和正有理數。因為不存在最小負有理數和正有理數，所以狄利克雷函式不存在最小正週期

　　黎曼函式：是一個特殊函式，由德國數學家黎曼發現提出，黎曼函式定義在 [0, 1]上。黎曼函式在高數中被廣泛應用，在很多情況下可以作為反例來驗證某些函式方面的待證命題。

　　其基本定義如下：

　　正態分佈：

　　（μ  是期望， σ² 是方差）

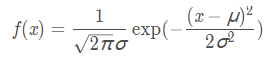
　　標準正態分佈：

　　（μ  是期望=0， σ² 是方差=1）

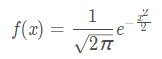
1.3 函式的特性

有界性

　　設函式 f(x) 在區間 X 上有定義，如果存在 M>0，對於一切屬於區間 X 上的 x，恆有 | f(x) | <= M，則稱 f(x) 在區間 X上有界，否則稱 f(x) 在區間上無界。

奇偶性

　　設 f(x) 為一個實變數實值函式，若此函式關於 y 軸對稱，則稱 f(x) 為偶函式。

　　　　　　 f(-x) = f(x)  

　　偶函式例子：

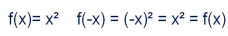
　　設 f(x) 為一個實變數實值函式，若此函式關於原點對稱，則稱 f(x) 為奇函式。

　　　　　　f(-x) = -f(x)

　　奇函式例子：

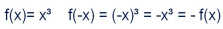
週期性

　　設函式 f(x) 的定義域為D。如果存在一個正數 T，使得對於任一 x 屬於 D 有 （x+-T）屬於D，且 f(x + T) = f(x)恆成立，則稱 f(x) 為周期函式， T稱為 f(x) 的週期，通常我們說周期函式是指最小正週期。公式如下：

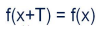
 　　周期函式的定義域 D為至少一邊的無界區間，若 D 為有界的，則該函式不具週期性。並非每個周期函式都有最小正週期，例如狄利克雷函式。

單調性

　　設函式 f(x) 的定義域為 D，區間 I 包含於 D。如果對於區間上任意兩點 x1 及 x2，當 x1 < x2 時，恆有 f(x1) < f(x2)，則稱函式 f(x) 在區間 I 上是單調遞增的；如果對於區間 I 上任意兩點 x1 及 x2，當 x1 < x2時，恆有 f(x1) > f(x2)，則稱函式 f(x) 在區間 I 上是單調遞減的。單調遞增和單調遞減函式統稱為 單調函式。

1.4   函式的極限

　　學習極限之前，先看一下數列：

數列

　　數列（sequence of number）是以正整數集為定義域的函式，是一列有序的數；即按照一定次數排列的一列數：u1, u2, ... u_n, ...，其中 排在第一位的數列為這個數列的第一項（也叫首項）， u_n 叫做通項。

　　著名的數列有：斐波那契數列，三角函式，楊輝三角等。

　　對於數列 {u_n} ，如果當 n 無限增大時，其通項無限接近於一個常數 A，則稱該數列以 A 為極限或稱數列收斂於 A，否則稱數列為發散：

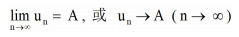
 　　舉個例子：

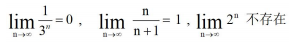
函式極限

　　極限定義：設函式 f(x) 在點 x0 的某一去心鄰域內有定義，如果存在常數A，對於任意給定的正數 ε （無論它多麼小），總存在正數 δ ，使得當 x 滿足不等式 0 < |x - x0| < δ 時，對應的函式值 f(x) 都滿足不等式：

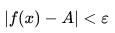
　　那麼常數 A 就叫做函式 f(x) 當 x——> x0 時的極限，記做：

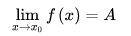
　　函式極限可以分為下面六種：

1.5 極限存在準則

　　有些函式的極限很難或難以直接運用極限運算求得，需要先判定。下面學習幾個常用的判定數列極限的定理。

1.5.1  夾逼定理

　　（1） 當 x € U(x₀, r) （這是 x₀ 的去心鄰域，有個符號打不出）時，有下面公式成立：

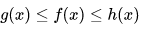
　　（2） f(x) 極限存在，且等於A 的條件是：

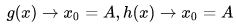
　　簡單說：就是找出一個比原式小的式子和一個比原式大的式子證明他們倆的極限相同且為a，則原式極限也為 a。

1.5.2  單調有界準則

　　單調增加（減少）有上（下）界的數列必定收斂。

　　在運用上面兩條去求函式的極限的時候尤其需要注意以下關鍵點。一是要用單調有界定理證明收斂，然後再求極限值。二是應用夾逼定理的關鍵是找出極限相同的函式，並且要滿足極限是趨於同一方向，從而證明或求得函式的極限值。

　　單調有界定理：單調有界數列必收斂（有極限）。具體的說：

　　（1）若數列 {Xn} 遞增且有上界，則：

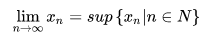
　　（2）若數列 {Xn} 遞減且有下界，則：

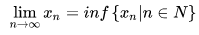
1.5.3  柯西收斂準則

　　數列 {Xn} 收斂的充分必要條件是：對於任意給定的正數 ε ，總存在正整數  N，使得當 m>N，n>N時，且 m≠n，有 |Xm - Xn| < ε。我們把滿足該條件的 {Xn} 稱為柯西序列，那麼上述定理可以表述為：數列{Xn}收斂，當且僅當它是一個柯西序列。

1.6 課程中的PPT

1.7  常見函式極限公式

　　首先說一下常見函式求極限的方法：

• 1，分母極限為零時，分解因式，湊公式
• 2，當 x 趨於無窮時，除以最高指數的 Xⁿ
• 3，等價無窮小量代換：

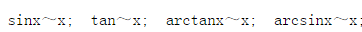
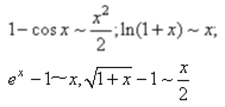
　　下面看一下常見函式極限公式：

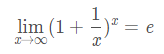
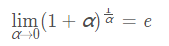
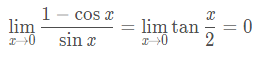
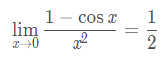
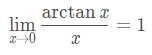
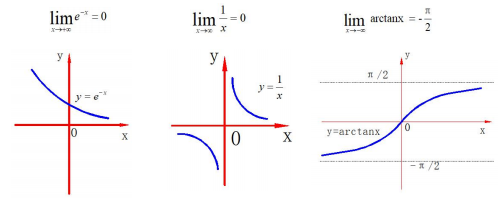
2，函式連續性與間斷點

2.1  函式連續性定義

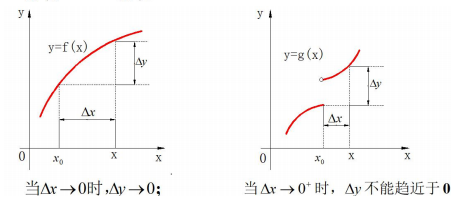
　　設函式 f 在某鄰域 U(x₀) 內有定義，若當自變數的改變數 Δx 趨於零時，相應函式的改變數 Δy 也趨近於零，則稱 y=f(x) 在點 x 處連續：

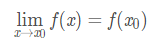
　　則稱 f 在點 x₀ 處連續。

　　函式連續必須同時滿足三個條件：

• 1，函式在 x0 處有定義
• 2，x->x0時候，函式在該點處極限 lim f(x) 存在
• 3，x->x0時候，函式在該點處極限值 lim f(x) 等於函式值 f(x0)

　　定理1：函式 f 在點 x₀ 處連續性的充要條件是：f 在點 x₀ 既是左連續，又是右連續。

　　初等函式在其定義域內是連續的；函式 f(x) 在其定義域內每一點都連續，則稱函式 f(x) 為連續函式。下圖左為連續函式，右圖為間斷函式。

2.2  函式間斷點

　　設函式 f 在某 U⁰(x₀) 內有定義，若 f 在點 x0 無定義，或在點 x0 有定義而不連續，則稱點 x0 為函式 f 的間斷點或不連續點。

　　函式間斷點分為兩種情況：

　　1，可去間斷點：若：

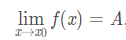
　　而 f 在點 x₀ 處無定義，或有定義但 f(x₀) != A ，則稱 x₀ 為 f 的可去間斷點。

　　2，跳躍間斷點：若函式 f 在點 x0 的左，右極限都存在，但：

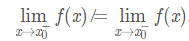
 　　則稱點 x0 為函式 f 的跳躍間斷點。

　　可去間斷點和跳躍間斷點統稱為第一類間斷點。第一類間斷點的特點是函式在該點處的左右極限都存在。

　　函式的所有其他形式的間斷點，即使得函式至少有異側極限不存在的那些點，稱為第二類間斷點。

2.3  課程中的PPT

　　下面為連續性和間斷點的兩個例子：

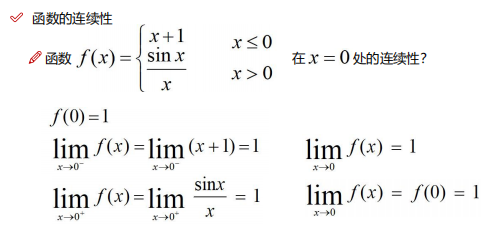
3，導數

3.1  導數定義

　　設函式 y = f(x) 在點 x₀ 的某鄰域內有定義，若極限：

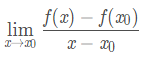
　　存在，則稱函式 f 在點 x₀ 處可導，並稱該極限為函式 f 在點 x₀ 處的導數，記為 f '(x₀)

　　f'(x) 也可以定義如下：

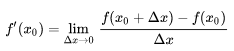
3.2  左右導數的幾何意義和物理意義

　　函式 f(x) 在 x₀ 處的左，右導數分別定義為：

　　左導數：

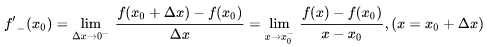
　　右導數：

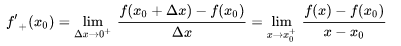
3.3 常用導數公式

　　常用求導公式：

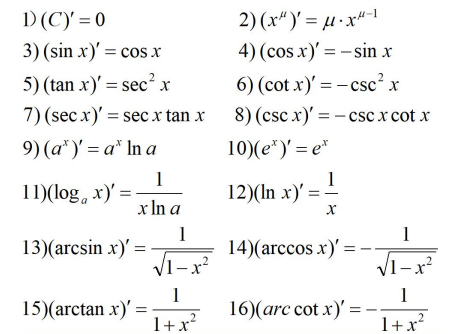
3.4  導數的四則運演算法則

　　設 u = u(x)， v = v(x) 均為 x 的可導函式，則有：

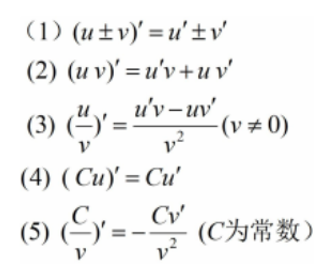
3.5  函式的可導性與連續性之間的關係

　　即連續是可導的必要條件，即函式可導必然連續；不連續必然不可導‘連續不一定可導。

　　主要為以下幾個定理：

　　定理1：若函式 f 在點 x₀ 處可導，則 f 在點 x₀ 處連續。

　　注意：可導僅僅是函式在該點連續的充分條件，而不是必要條件，如函式 f(x) = |x| 在點 x=0 處連續，但不可導。

　　定理2：若函式 y = f(x) 在點 x0 的某鄰域內有定義，則 f'(x₀) 存在的充要條件是 f '₊(x₀) 與 f '_-(x₀) 都存在，且：

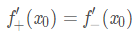
　　定理3（費馬定理）：設函式 f 在點 x₀ 的某鄰域內有定義，且在點 x₀ 處可導，若點 x₀ 為 f 的極值點，則必有：

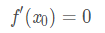
　　我們稱滿足方程 f ' = 0 的點 o 為穩定點。

　　定理4：函式 f 在點 x₀ 可微的充要條件是函式 f 在點 x₀ 可導，而且常量 A等於 f '(x₀)

4，梯度

　　在學習梯度之前，先學習兩個基本概念

4.1 偏導數

　　在數學中，一個多變數的函式的偏導數，就是它關於其中一個變數的導數而保持其他變數恆定（相對於全導數，在其中所有變數都允許變換）。偏導數在向量分析和微分幾何中是很有用的。

　　在一元函式中，導數就是函式的變化率。如下圖所示，對於一元函式 y = f(x) 只存在 y 隨 x 的變化：

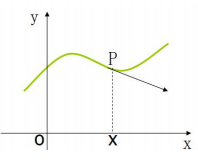
　　二元函式 z = f(x, y) 存在 z 隨 x 變化的變化率，隨 y 變化的變化率，隨 x,  y 同時變化的變化率：

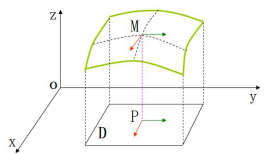
　　在 XOY 平面內，當動點由 P(x0, y0) 沿不同方向變化時，函式 f(x, y) 的變化快慢一般來說是不同的，因此就需要研究 f(x, y) 在 (x0, y0) 點處沿不同方向的變化率。在這裡我們只學習函式 f(x, y) 沿著平行於 x 軸和平行於 y 軸兩個特殊方位變動時，f(x, y) 的變化率。

　　偏導數的表示符號為：∂

　　偏導數反映的是函式沿著座標軸正方向的變化率。

　　方向x的偏導定義：設存在函式  z = f(x, y) 在點 (x0, y0) 的某個鄰域內有定義，固定 y=y0，而讓x 在 x0 出有增量，則相應的函式 z=f(x, y) 有增量，那麼增量表示為：Δz = f(x0+Δx, y0) - f(x0, y0)。

　　如果 Δz 與 Δx 之比，當 Δx->0 時的極限存在，那麼此極限值稱為函式 z=f(x, y)在 (x0, y0) 處對 x 的偏導數，記做 f '_x(x0, y0) 或者函式 z = f(x, y) 在 (x0, y0) 處對 x 的偏導數，實際上就是把 y 固定在 y0 看成常數後，一元函式 f(x, y0) 在點 x = x0 處可導，即極限：

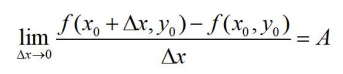　　則稱A為函式 Z=f(x, y) 在點 (x0, y0) 處關於自變數 x 的偏導數，記做：f_x(x0, y0)，或者：

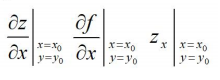　　y方向的偏導：同理，把 x 固定在 x0，讓 y 有增量 Δy，如果極限存在那麼此極限稱為函式 z = f(x, y) 在 (x0, y0) 處對 y 的偏導數，記做 f'_y(x0, y0)。

　　幾何意義：表示固定面上一點的切線斜率。

　　偏導數 f '_x(x0, y0) 表示固定面上一點對 x 軸的切線斜率

　　偏導數 f'_y(x0, y0) 表示固定面上一點對 y 軸的切線斜率

 　　下面給個例子，求偏導數：

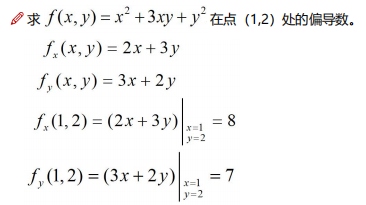
4.2  方向導數

　　在函式定義域的內點，對某一方向得到的導數。一般為二元函式和三元函式的方向導數，方向導數可分為沿直線方向和沿曲線方向的方向導數。

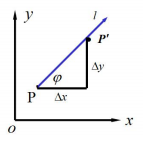
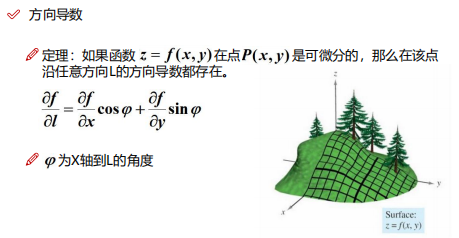
　　定義：設函式 z = f(x, y) 在點 p(x, y) 的某一鄰域 U(p) 內有定義，自點 p 引射線 l，自 x 軸的的正向到射線 l 的轉角為 Ψ。P '(x + Δx, y + Δy) 為 l 上的另一點，若存在：

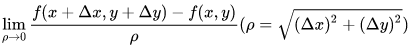
　　則稱此極限值為 f(x, y) 在點 P 沿方向 l 的方向導數，記做 ∂f / ∂l，其計算公式為：

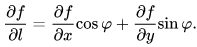
　　沿直線方向：設 M0 = (x0, y0, z0) 為數量場  u=u(M) 中的一點，從點 M0 出發引一條射線 l（其方向用 l 表示），在 l 上點 M0 的鄰近取一動點 M(x0 + Δx, y0 + Δy， z0 + Δz)，記：

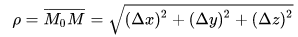
　　如圖所示，若當 M -> M0 時，下分式的極限存在，則稱它為函式 u(M) 在點 M0 處沿 l 方向的方向導數，記做 ∂f / ∂l|M0,即：

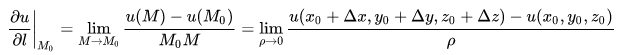
4.3  梯度

　　梯度的本意是一個向量（向量），表示某一函式在該點處的方向導數沿著該方向取得最大值，即函式在該點處沿著該方向（此梯度的方向）變化最快，變化率最大（為該梯度的模）。

　　函式 z = f(x, y) 在平面域內具有連續的一階偏導數，對於其中每一個點 P(x, y) 都可以定出一個向量：

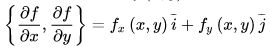　　該函式就稱為函式 z = f(x, y) 在點 P(x, y) 的梯度，記為 gradf(x, y)。

數學分析筆記：https://blog.csdn.net/weixin_37411514/article/details/97903625