線性迴歸-如何對資料進行迴歸分析
阿新 • • 發佈:2020-12-21
> **公號:碼農充電站pro**
> **主頁:**
**線性迴歸模型**用於處理迴歸問題,也就是預測連續型數值。線性迴歸模型是最基礎的一種迴歸模型,理解起來也很容易,我們從**解方程組**談起。
### 1,解方程組
相信大家對**解方程**都不陌生,這是我們初中時期最熟悉的數學知識。
假如我們有以下方程組:
- 2x + y = 3 —— ①
- 5x - 2y = 7 —— ②
要解上面這個方程組,我們可以將第一個方程的等號兩邊都乘以2:
- 4x + 2y = 6 —— ③
再將第2 個方程與第3 個方程的等號兩邊分別相加:
- 9x = 13 —— ④
這樣我們就將**變數y 消去**了,就可以求解出**x** 的值。然後再將**x** 的值**代入**第1或第2個方程中,就可以解出**y** 的值。
以上這個解方程的過程就是**高斯消元法**。
### 2,線性迴歸模型
如果將上面方程組中的任意一個表示式單拿出來,那麼**x** 和 **y** 都是一種**線性**關係,比如:
- y = 3 - 2x
該表示式中,我們將**x** 叫做**自變數**,**y** 叫作**因變數**。
如果將其擴充套件到機器學習中,那麼**特徵集**就相當於**自變數X**,**目標集**就相當於**因變數Y**。
當自變數的個數大於1時,就是**多元迴歸**;當因變數的個數大於1 時,就是**多重回歸**。
**線性迴歸模型**的目的就是想找出一種**特徵集**與**目標集**之間的**線性關係**,使得我們可以通過已知的特徵資料預測出目標資料。
通常,我們的模型是通過多個特徵值來預測一個目標值,那麼線性迴歸模型的數學公式為:
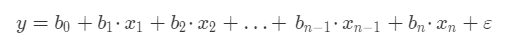
其中:
- y 表示我們要預測的目標值。
- x1,x2...xn 代表每個特徵,一共有n 個特徵。
- b1,b2...bn 代表每個特徵的係數,特徵係數也代表了某個特徵對目標值的影響。
- b0 是一個常數,稱為截距。
- ε 表示模型的誤差,也被稱作損失函式。
線性迴歸模型與數學中的解方程不同,後者的結果是精確解,而前者則是一個近似解。因此在公式中存在一個 **ε** 。
我們的目標是求得一組使得 **ε** 最小的特徵係數(b1,b2...bn),當有了新的特徵時,就可以根據特徵係數求得預測值。
***迴歸一詞的來源***
**1875** 年,英國科學家**弗朗西·斯高爾頓**(達爾文的表弟)嘗試尋找父代身高與子代身高之間的關係。
在經過了**1078** 份資料的分析之後,最終他得出結論:人類的身高維持在相對穩定的狀態,他稱之為**迴歸效應**,並給出了歷史上第一個**迴歸**公式:
- `Y = 0.516X + 33.73`
公式中的 **Y** 代表子代身高,**X** 代表父代身高,單位為英寸。
### 3,線性擬合
線性擬閤中不存在精確解,但是存在最優解,也就是使得 **ε** 最小的解。
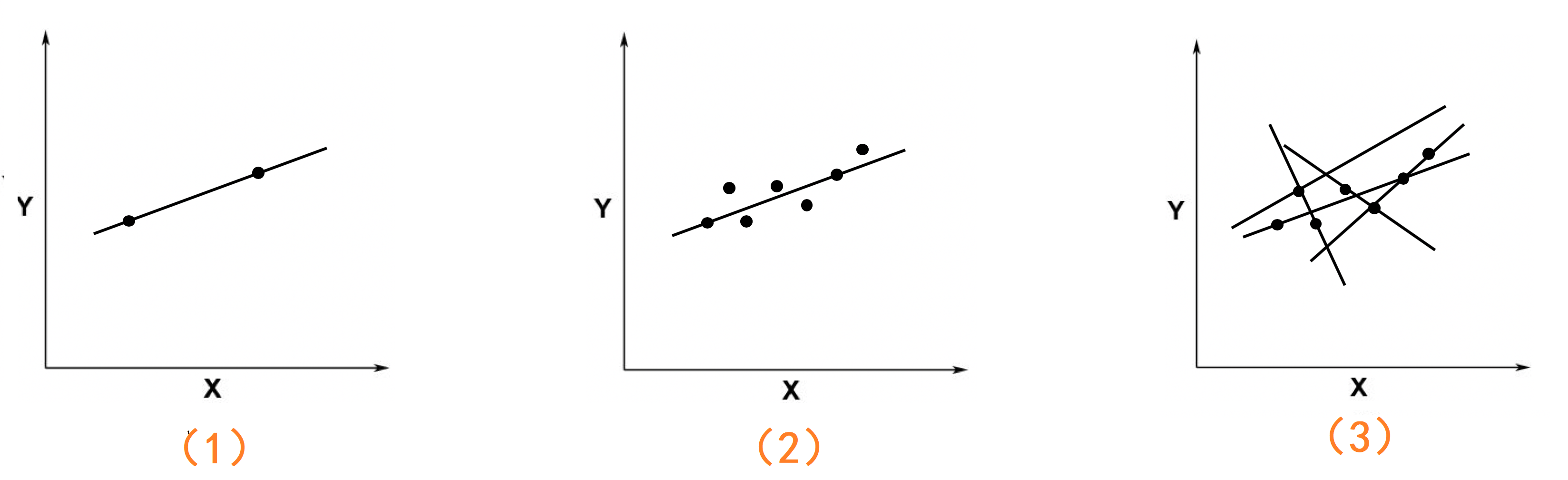
上圖中有3 個座標系:
- 在第1個圖中只有兩個點,這時候存在一條唯一的直線能夠同時穿過這兩個點,這條直線就是精確解。
- 當座標中的點多於兩個時,比如第2個圖,這時候就不可能存在一條直線,同時穿過這些點。但是會存在多條直線,會盡可能多的穿過更多的點,就像圖3。而這些直線中會有一條直線,是這些點的最好的**擬合**。
如何才能找到這條最好的擬合的直線呢?
### 4,最小二乘法
**最小二乘法**可以用來求解這個最優直線。
最小二乘法的主要思想是讓**真實值**與**預測值**之差(即誤差)的平方和達到最小。用公式表示如下:
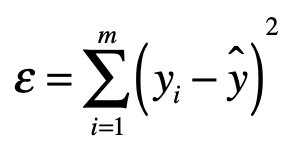
上面的公式中:
- yi
