[TJOI2013]攻擊裝置
阿新 • • 發佈:2020-12-22
# 前言
沒啥好說的,[題目連結](https://www.luogu.com.cn/problem/P4304)。
# 題目簡述
$n$ 行 $n$ 列的矩陣中,若該點為 $0$ ,則可以安放裝置 $(x,y)$ ,若裝置會攻擊$(x-1,y-2)$ , $(x-2,y-1)$ , $(x+1,y-2)$ , $(x+2,y-1)$ , $(x-1,y+2)$ , $(x-2,y+1)$ , $(x+1,y+2)$ , $(x+2,y+1)$ 這八個位置的裝置。求最多可以放多少裝置。
# 思路
最開始時,沒啥思路,將一個裝置在一張圖中表示出來,攻擊範圍如下:
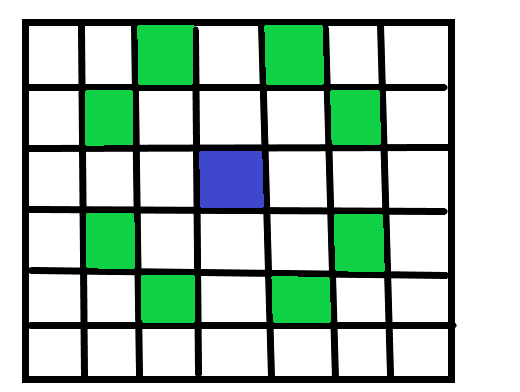
綠色點為藍色點能夠攻擊到的點。可以發現很像國際象棋的棋盤,進一步做如下染色:

這樣對比兩張圖,可以發現,白色點可以能夠攻擊到的點全都是黑色點,黑色點可以能夠攻擊到的點全都是白色點。白色點與白色點、黑色點與黑色點之間不會有聯絡。
這樣的兩個同一集合內的點互不關聯,且有兩個集合的問題不難轉換成二分圖來求解。其中,不妨設白色點為左部點,黑色點為右部點,構建一張二分圖。
求解的問題是最大的互不攻擊的裝置,即可以轉換為二分圖的最大獨立集問題。而最大獨立集的點數等於二分圖中所有點的個數減去最大匹配的邊數,進而用網路最大流來求解。
# C++程式碼
```cpp
#include
#include
#include
#include
using namespace std;
#define INF 0x3f3f3f3f
#define Min(a, b) ((a) < (b) ? (a) : (b))
void Quick_Read(int &N) {
N = 0;
int op = 1;
char c = getchar();
while(c < '0' || c > '9') {
if(c == '-')
op = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
N = (N << 1) + (N << 3) + (c ^ 48);
c = getchar();
}
N *= op;
}
void Read_OneNumber(int &N) {
N = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
N = c ^ 48;
}
const int MAXN = 2e2 + 5;
const int MAXM = 4e4 + 5;
const int MAXK = 10;
int color[MAXN][MAXN];
int addx[MAXK] = {0, -1, -2, 1, 2, -1, -2, 1, 2};
int addy[MAXK] = {0, -2, -1, -2, -1, 2, 1, 2, 1};
int n, Sum;
struct Node {
int to, val, rev;
Node() {}
Node(int T, int V, int R) {
to = T;
val = V;
rev = R;
}
};
vector v[MAXM];
queue q;
int be[MAXM], de[MAXM];
int s, t;
bool Bfs_Dinic() {//將殘量網路分層
while(!q.empty())
q.pop();
memset(de, 0, sizeof(de));
q.push(s);
de[s] = 1;
be[s] = 0;
while(!q.empty()) {
int now = q.front(); q.pop();
int SIZ = v[now].size();
for(int i = 0; i < SIZ; i++) {
int next = v[now][i].to;
if(!de[next] && v[now][i].val) {
be[next] = 0;
de[next] = de[now] + 1;
q.push(next);
if(next == t)
return true;
}
}
}
return false;//找不到增廣路
}
int Dfs_Dinic(int now, int flow) {//在殘量網路中尋找增廣路並增廣
if(now == t || !flow)
return flow;
int surp = flow;
int SIZ = v[now].size();
for(int i = be[now]; i < SIZ && surp; i++) {
be[now] = i;//弧優化
int next = v[now][i].to;
if(v[now][i].val && de[next] == de[now] + 1) {
int maxnow = Dfs_Dinic(next, Min(surp, v[now][i].val));
if(!maxnow)
de[next] = -1;
v[now][i].val -= maxnow;
v[next][v[now][i].rev].val += maxnow;
surp -= maxnow;
}
}
return flow - surp;
}
int Dinic() {//最大流
int res = 0, flow;
while(Bfs_Dinic())
while(flow = Dfs_Dinic(s, INF))
res += flow;
return res;
}
int Serial_Number(int i, int j) {//求該點的邊號,勉強算個hash
return (i - 1) * n + j;
}
void Read() {
Quick_Read(n);
s = 0; t = n * n + 1;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++) {
Read_OneNumber(color[i][j]);
Sum += !color[i][j];
}
for(int i = 1; i <= n; i++)//構建二分圖
for(int j = 1; j <= n; j++) {
if(color[i][j] || !((i + j) & 1))
continue;
int now = Serial_Number(i, j);
for(int k = 1; k <= 8; k++) {
if(i + addx[k] < 1 || i + addx[k] > n || j + addy[k] < 1 || j + addy[k] > n)
continue;
int next = Serial_Number(i + addx[k], j + addy[k]);
if(color[i][j])
continue;
int id1 = v[now].size();
int id2 = v[next].size();
v[now].push_back(Node(next, 1, id2));
v[next].push_back(Node(now, 0, id1));
}
}
for(int i = 1; i <= n; i++)//構建網路
for(int j = 1; j <= n; j++) {
if(color[i][j])
continue;
int now = Serial_Number(i, j);
int idn = v[now].size();
if((i + j) & 1) {
int ids = v[s].size();
v[s].push_back(Node(now, 1, idn));
v[now].push_back(Node(s, 0, ids));
}
else {
int idt = v[t].size();
v[now].push_back(Node(t, 1, idt));
v[t].push_back(Node(now, 0, idn));
}
}
}
void Write() {
printf("%d", Sum - Dinic());//二分圖最大獨立集
}
int main() {
Read();
Write();
return
