一、為什麼要正則化

　　學習演算法，包括線性迴歸和邏輯迴歸，它們能夠有效地解決許多問題，但是當將它們應用到某些特定的機器學習應用時，會遇到過擬合(over-fitting)的問題，可能會導致它們效果很差。正則化(regularization)技術，可以改善或者減少過度擬合問題，進而增強泛化能力。泛化誤差（generalization error）= 測試誤差（test error），其實就是使用訓練資料訓練的模型在測試集上的表現（或說效能 performance）好不好。

　　如果我們有非常多的特徵，我們通過學習得到的假設可能能夠非常好地適應訓練集（代價函式可能幾乎為0），但是可能會不能推廣到新的資料。

　　下圖是一個迴歸問題的例子：

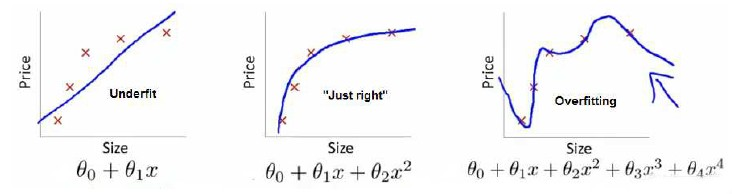
　　第一個模型是一個線性模型，欠擬合，不能很好地適應我們的訓練集；第三個模型是一個四次方的模型，過於強調擬合原始資料，而丟失了演算法的本質：預測新資料。我們可以看出，若給出一個新的值使之預測，它將表現的很差，是過擬合，雖然能非常好地適應我們的訓練集但在新輸入變數進行預測時可能會效果不好；而中間的模型似乎最合適。

　　分類問題中也存在這樣的問題：

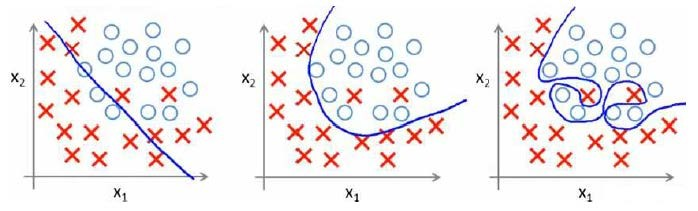
就以多項式理解，$x$的次數越高，擬合的越好，但相應的預測的能力就可能變差。

　　如果我們發現了過擬合問題，可以進行以下處理：

　　1、丟棄一些不能幫助我們正確預測的特徵。可以是手工選擇保留哪些特徵，或者使用一些模型選擇的演算法來幫忙（例如PCA）。

　　2、正則化。 保留所有的特徵，但是減少引數的大小（magnitude）。

二、正則化的定義

　　正則化的英文 Regularizaiton-Regular-Regularize，直譯應該是"規則化"，本質其實很簡單，就是給模型加一些規則限制，約束要優化引數，目的是防止過擬合。其中最常見的規則限制就是新增先驗約束，常用的有L1範數和L2範數，其中L1相當於新增Laplace先驗，L相當於新增Gaussian先驗。 

三、L1正則和L2正則

　　在介紹L1範數、L2範數之前，我們先介紹以下LP範數。

　　3.1 範數

　　範數簡單可以理解為用來表徵向量空間中的距離，而距離的定義很抽象，只要滿足非負、自反、三角不等式就可以稱之為距離。

　　LP範數不是一個範數，而是一組範數，其定義如下：

$\left \| x \right \|_{p}=(\sum_{i}^{n}x_{i}^{p})^{\frac{1}{p}}$ 

$\left \| x \right \|_{p}=(\sum_{i}^{n}x_{i}^{p})^{\frac{1}{p}}$ 

$p$的範圍是[1,∞)[1,∞)。$p$在(0,1)(0,1)範圍內定義的並不是範數，因為違反了三角不等式。

　　根據$p$的變化，範數也有著不同的變化，借用一個經典的有關P範數的變化圖如下： 

　　上圖表示了$p$從0到正無窮變化時，單位球（unit ball）的變化情況。在P範數下定義的單位球都是凸集，但是當0<