>原創公眾號：[bigsai](https://mp.weixin.qq.com/s/IW_GNK254ijIuuupjJsKCA) > 文章已收錄在 [全網都在關注的資料結構與演算法學習倉庫](https://github.com/javasmall/bigsai-algorithm) 歡迎star ## 前言 位運算隱藏在程式語言的角落中，其神祕而又強大，暗藏內力，有些人光聽位運算的大名的心中忐忑，還有些人更是一看到位運算就遠遠離去，我之前也是。但狡猾的面試官往往喜歡搞偷襲，抓住我們的弱點搞我們，為了防患於未然，特記此篇！ 本篇的內容為位運算的介紹和一些比較經典的位運算問題進行介紹分析，當然，位運算這麼牛，後面肯定還是要歸納總結的。 ## 認識位運算 什麼是位運算？ > 程式中的所有數在計算機記憶體中都是以二進位制的形式儲存的。位運算就是直接對整數在記憶體中的二進位制位進行操作。 位運算就是直接操作二進位制數，那麼有哪些種類的位運算呢？ 常見的運算子有與(&)、或(|)、異或(^)、取反(~)、左移(<<)、右移(>>是帶符號右移 >>>無符號右移動)。下面來細看看每一種位運算的規則。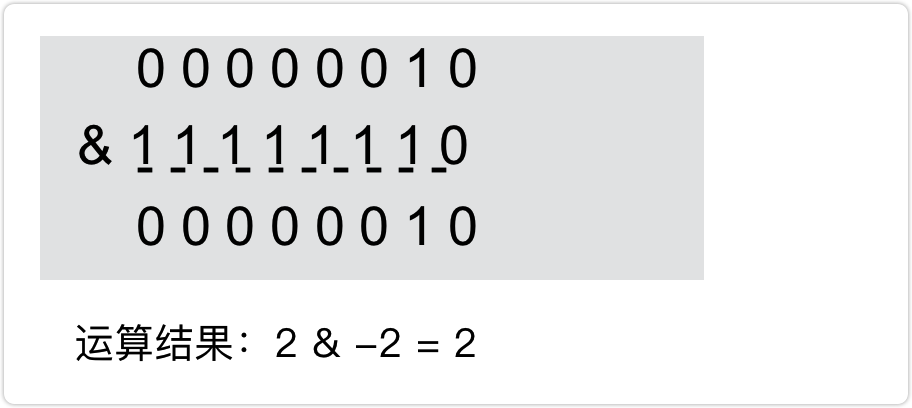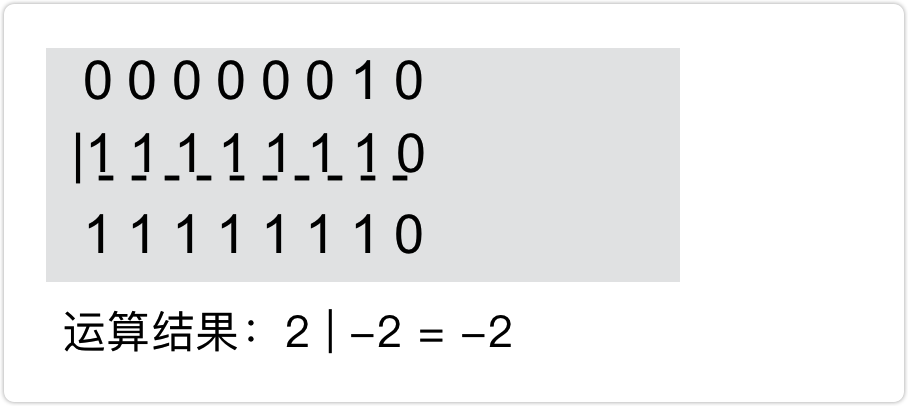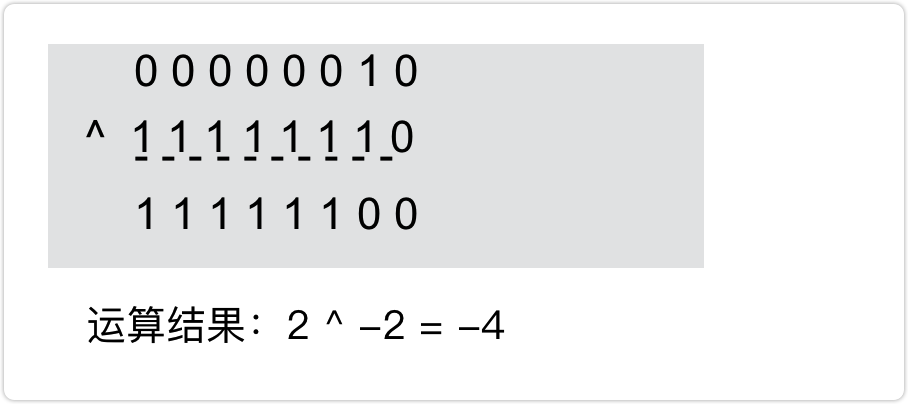 **位運算 & (與)** 規則：二進位制對應位兩兩進行邏輯AND運算(只有對應位的值都是 1 時結果才為 1, 否則即為 0)即 `0&0=0`,` 0&1=0`,` 1&1=1` 例如：2 & -2  **位運算 | (或)** 規則：二進位制對應位兩兩進行邏輯或運算(對應位中有一 個為1則為1) 即`0|0=0`,`0|1=1`,`1|1=1` 例如：2 | -2  **位運算 ^ (異或)** 規則：二進位制對應位兩兩進行邏輯XOR (異或) 的運算(當對應位的值不同時為 1, 否則為 0)即`0^0=0`, `0^1=1`, ` 1^1=0` 例如：2 ^ -2  **按位取反~** 規則：二進位制的0變成1，1變成0。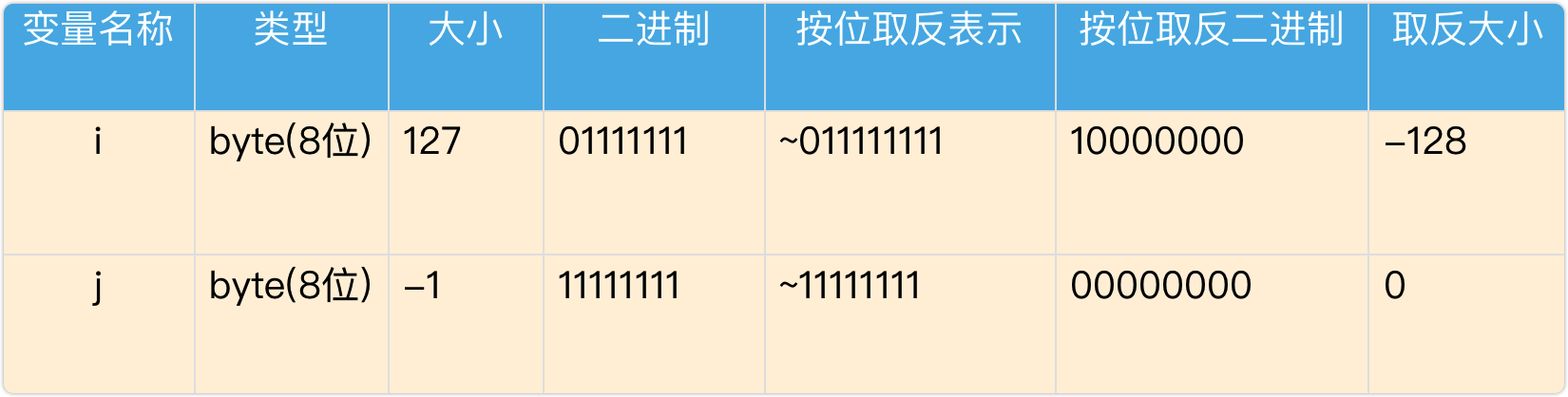  **移位運算子** 左移運算`<<`：左移後右邊位補 0 右移運算`>>`：右移後左邊位補**原最左位值(可能是0，可能是1)** 右移運算`>>>`：右移後左邊位補 0 - 對於左移運算子`<<`沒有懸念右側填個零無論正負數相當於整個數乘以2。 - 而右移運算子就有分歧了，分別是左側補0`>>>`和左側補原始位`>>`，如果是正數沒爭議左側都是補0，達到除以2的效果；如果是負數的話左側補0`>>>`那麼數值的正負會發生改變，會從一個負數變成一個相對較大的正數。而如果是左側補原始位(負數補1)`>>`那麼整個數還是負數，也就是相當於除以2的效果。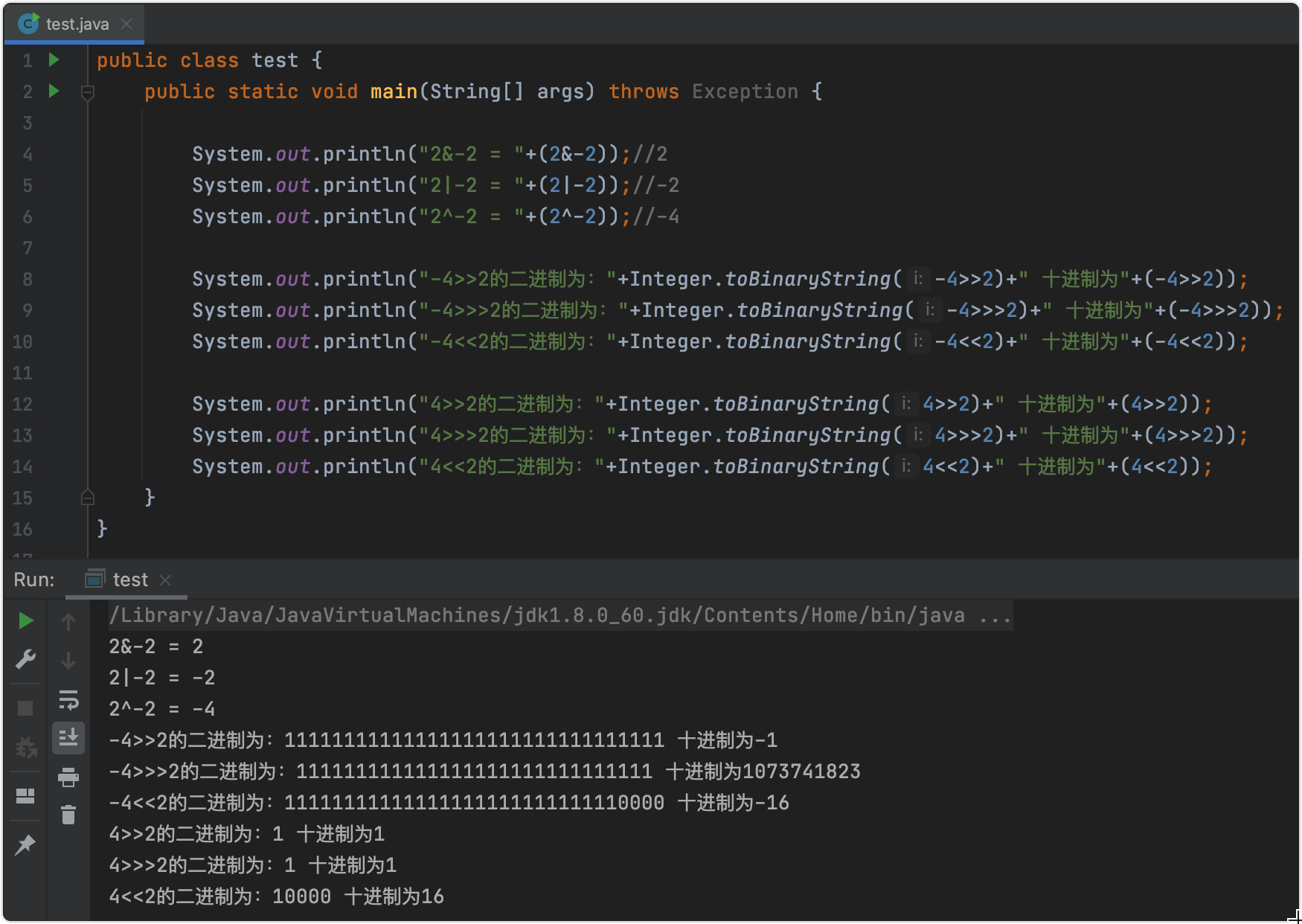 下面這張圖可以很好的幫助你理解負數的移位運算子：  到這裡，我想你應該對位運算有了初步的認識，在這裡把上面提到的部分案例執行對比一下讓你看一下可能會理解的更清晰：  ## 位運算小技巧 在這裡有些常用的位運算小技巧。 ### 判斷奇偶數 正常判斷奇數偶數的時候我們會這樣寫： ```java if( n % 2 == 1) // n 是個奇數 } ``` 使用位運算可以這麼寫： ```java if(n & 1 == 1){ // n 是個奇數。 } ``` 其核心就是判斷二進位制的**最後一位是否為1**，如果為1那麼結果加上2^0=1一定是個奇數，否則就是個偶數。 ### 交換兩個數 對於傳統的交換兩個數，我們需要使用一個變數來輔助完成操作，可能會是這樣： ```java int team = a; a = b; b = team; ``` 但是使用位運算可以不需要藉助額外空間完成數值交換： ```java a=a^b;//a=a^b b=a^b;//b=(a^b)^b=a^0=a a=a^b;//a=(a^b)^(a^b^b)=0^b=0 ``` 原理已經寫在註釋裡面了，是不是感覺非常diao呢？ ### 二進位制列舉 在遇到子集問題的處理時候，我們有時候會藉助二進位制列舉來遍歷各種狀態(效率大於dfs回溯)。這種就屬於排列組合的問題了，對於每個物品(位置)來說，就是使用和不使用的兩個狀態，而在二進位制中剛好可以用1和0來表示。而在實現上，通過列舉數字範圍分析每個二進位制數字各符號位上的特徵進行計算求解操作即可。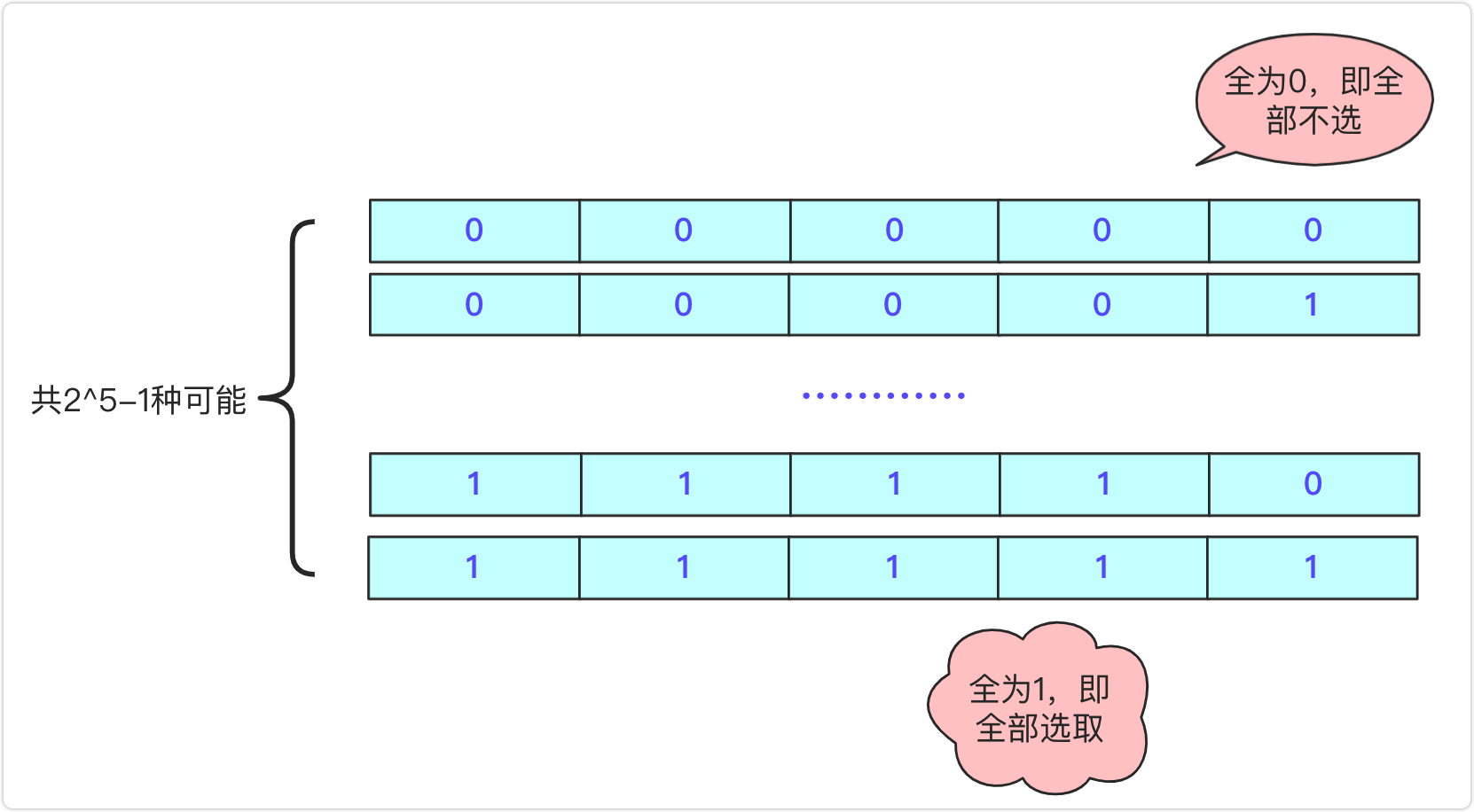  二進位制列舉的程式碼實現為： ```java for(int i = 0; i <