作為一個標準的程式設計師，應該有一些基本的數學素養，尤其現在很多人在學習人工智慧相關知識，想抓住一波人工智慧的機會。很多程式設計師可能連這樣一些基礎的數學問題都回答不上來。 - 矩陣`A(m,n)`與矩陣`B(n,k)`乘積C維度是多少？ - 拋一枚硬幣，正面表示1，反面表示0，那麼取值的數學期望E(x)是多少？ 作為一個傲嬌的程式設計師，應該要掌握這些數學基礎知識，才更有可能碼出一個偉大的產品。 ## 線性代數 **向量** 向量（vector）是由一組實陣列成的有序陣列，同時具有大小和方向。一個n維向量a是由n個有序實陣列成，表示為 a = [a1, a2, · · · , an] **矩陣** **線性對映** 矩陣通常表示一個n維線性空間v到m維線性空間w的一個對映f: v -> w 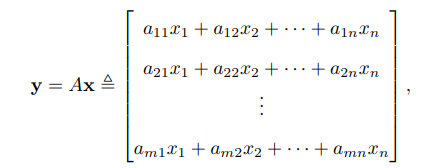 注：為了書寫方便，`X.T`，表示向量X的轉置。 這裡：`X(x1,x2,...,xn).T，y(y1,y2,...ym).T`，都是列向量。分別表示v,w兩個線性空間中的兩個向量。A(m,n)是一個`m*n`的矩陣，描述了從v到w的一個線性對映。 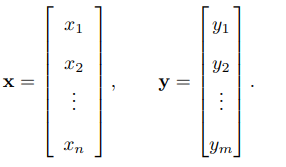 **轉置** 將矩陣行列互換。 **加法** 如果A和B 都為m × n的矩陣，則A和B 的加也是m × n的矩陣，其每個元素是A和B相應元素相加。 [A + B]ij = aij + bij . **乘法** 如A是k × m矩陣和B 是m × n矩陣，則乘積AB 是一個k × n的矩陣。 **對角矩陣** 對角矩陣是一個主對角線之外的元素皆為0的矩陣。對角線上的元素可以為0或其他值。一個n × n的對角矩陣A滿足： [A]ij = 0 if i ̸= j ∀i, j ∈ {1, · · · , n} **特徵值與特徵向量** 如果一個標量λ和一個非零向量v滿足 Av = λv, 則λ和v分別稱為矩陣A的特徵值和特徵向量。 **矩陣分解** 一個矩陣通常可以用一些比較“簡單”的矩陣來表示，稱為矩陣分解。 **奇異值分解** 一個m×n的矩陣A的奇異值分解 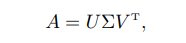 其中U 和V 分別為m × m和n×n 的正交矩陣，Σ為m × n的對角矩陣，其對角 線上的元素稱為奇異值（singular value）。 **特徵分解** 一個n × n的方塊矩陣A的特徵分解（Eigendecomposition）定義為 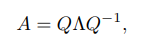 其中Q為n × n的方塊矩陣，其每一列都為A的特徵向量，^為對角陣，其每一 個對角元素為A的特徵值。 如果A為對稱矩陣，則A可以被分解為 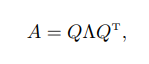其中Q為正交陣。 ## 微積分 **導數** 對於定義域和值域都是實數域的函式`f : R → R`，若f(x)在點x0 的某個鄰域∆x內，極限 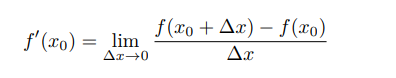存在，則稱函式f(x)在點x0 處可導，`f'(x0)`稱為其導數，或導函式。 若函式f(x)在其定義域包含的某區間內每一個點都可導，那麼也可以說函式f(x)在這個區間內可導。連續函式不一定可導，可導函式一定連續。例如函式|x|為連續函式，但在點x = 0處不可導。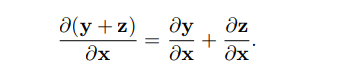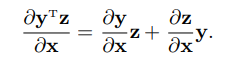 ### 導數法則 **加法法則** `y = f(x),z = g(x)`則  **乘法法則**  **鏈式法則** 求複合函式導數的一個法則，是在微積分中計算導數的一種常用方法。若`x ∈ R，y = g(x) ∈ R，z = f(y) ∈ R`，則 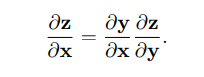 ### Logistic 函式 Logistic函式是一種常用的S形函式，是比利時數學家 Pierre François Verhulst在`1844-1845`年研究種群數量的增長模型時提出命名的，最初作為一種生 態學模型。 Logistic函式定義為： 當引數為`(k = 1, x0 = 0, L = 1)`時，logistic函式稱為標準logistic函式，記 為`σ(x)`。 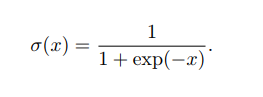標準logistic函式在機器學習中使用得非常廣泛，經常用來將一個實數空間的數對映到(0, 1)區間。標準`logistic`函式的導數為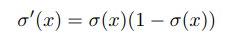：  ### softmax 函式 softmax函式是將多個標量對映為一個概率分佈。對於`K`個標量`x1, · · · , xK`，`softmax` 函式定義為 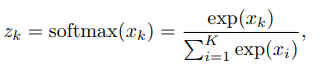這樣，我們可以將`K`個變數`x1, · · · , xK`轉換為一個分佈：`z1, · · · , zK`，滿足 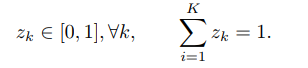當softmax 函式的輸入為K 維向量x時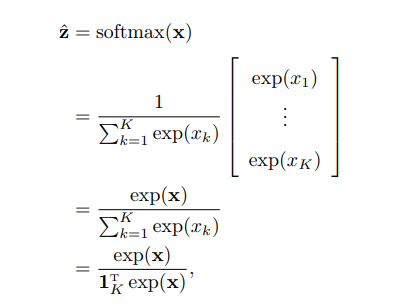， 其中，1K = [1, · · · , 1]K×1 是K 維的全1向量。其導數為  ## 數學優化 **離散優化和連續優化**:根據輸入變數x的值域是否為實數域，數學優化問題可以分為離散優化問題和連續優化問題。 **無約束優化和約束優化**:在連續優化問題中，根據是否有變數的約束條件，可以將優化問題分為無約束優化問題和約束優化問題。 ### 優化演算法 **全域性最優和區域性最優**海賽矩陣 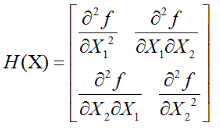《運籌學裡面有講》，前面一篇文章計算梯度步長的時候也用到了： 梯度下降演算法  ### 梯度 梯度的本意是一個向量（向量），表示某一函式在該點處的方向導數沿著該方向取得最大值，即函式在該點處沿著該方向（此梯度的方向）變化最快，變化率最大（為該梯度的模）。 **梯度下降法** 梯度下降法（Gradient Descent Method），也叫最速下降法（Steepest Descend Method），經常用來求解無約束優化的極小值問題。 梯度下降法的過程如圖所示。曲線是等高線（水平集），即函式f為不同常數的集合構成的曲線。紅色的箭頭指向該點梯度的反方向（梯度方向與通過該點的等高線垂直）。沿著梯度下降方向，將最終到達函式f 值的區域性最優解。 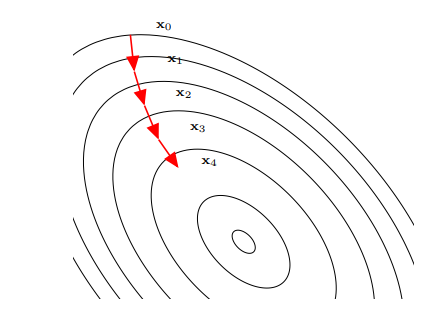 **梯度上升法** 如果我們要求解一個最大值問題，就需要向梯度正方向迭代進行搜尋，逐漸接近函式的區域性極大值點，這個過程則被稱為梯度上升法。 ## 概率論 概率論主要研究大量隨機現象中的數量規律，其應用十分廣泛，幾乎遍及各個領域。 **離散隨機變數**如果隨機變數X 所可能取的值為有限可列舉的，有n個有限取值 {x1, · · · , xn}, 則稱X 為離散隨機變數。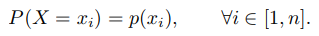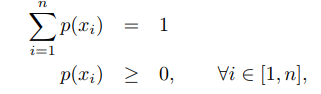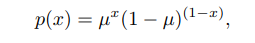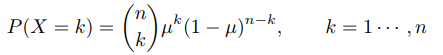要了解X 的統計規律，就必須知道它取每種可能值xi 的概率，即 `p(x1), · · · , p(xn)`稱為離散型隨機變數X 的概率分佈或分佈，並且滿足 常見的離散隨機概率分佈有： **伯努利分佈**  **二項分佈**  **連續隨機變數** 與離散隨機變數不同，一些隨機變數X 的取值是不可列舉的，由全部實數 或者由一部分割槽間組成，比如 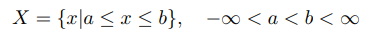則稱X 為連續隨機變數。 **概率密度函式** 連續隨機變數X 的概率分佈一般用概率密度函式`p(x)`來描述。`p(x)`為可積函式，並滿足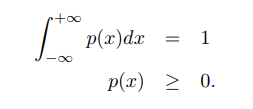：  **均勻分佈** 若a, b為有限數，[a, b]上的均勻分佈的概率密度函式定義為  **正態分佈** 又名高斯分佈，是自然界最常見的一種分佈，並且具有很多良好的性質，在很多領域都有非常重要的影響力，其概率密度函式為 其中，`σ > 0，µ`和`σ` 均為常數。若隨機變數X 服從一個引數為`µ`和`σ` 的概率分佈，簡記為 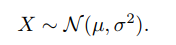當`µ = 0，σ = 1`時，稱為標準正態分佈。 均勻分佈和正態分佈的概率密度函式圖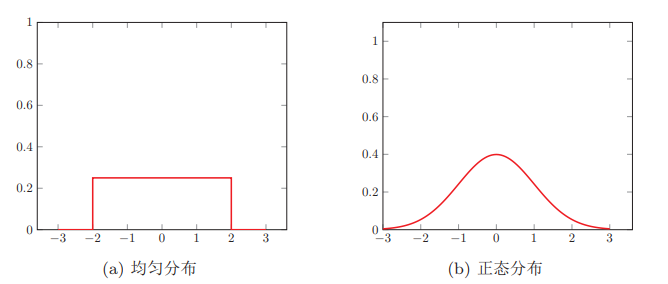：  **累積分佈函式** 對於一個隨機變數X，其累積分佈函式是隨機變數X 的取值小於等於x的概率。 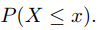以連續隨機變數X 為例，累積分佈函式定義為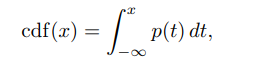： 其中p(x)為概率密度函式，標準正態分佈的累計分佈函式: 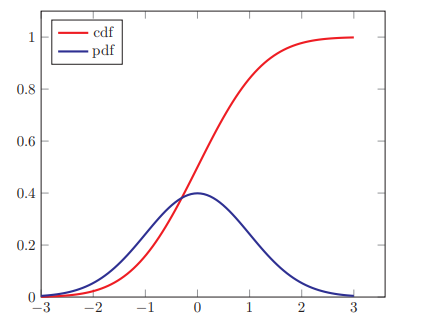 **隨機向量** 隨機向量是指一組隨機變數構成的向量。如果`X1, X2, · · · , Xn` 為n個隨機變數, 那麼稱 `[X1, X2, · · · , Xn]` 為一個 n 維隨機向量。一維隨機向量稱為隨機變數。隨機向量也分為離散隨機向量和連續隨機向量。 條件概率分佈 對於離散隨機向量`(X, Y)`，已知X = x的條件下，隨機變數`Y = y`的條件概率為： 對於二維連續隨機向量(X, Y )，已知X = x的條件下，隨機變數Y = y 的條件概率密度函式為 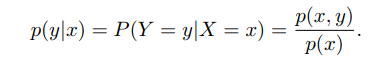 ### 期望和方差 **期望** 對於離散變數X，其概率分佈為`p(x1), · · · , p(xn)`，X 的期望（expectation）或均值定義為 對於連續隨機變數X，概率密度函式為p(x)，其期望定義為 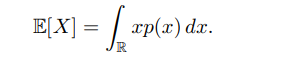 **方差** 隨機變數X 的方差（variance）用來定義它的概率分佈的離散程度，定義為  **標準差** 隨機變數 X 的方差也稱為它的二階矩。X 的根方差或標準差。 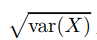 **協方差** 兩個連續隨機變數X 和Y 的協方差（covariance）用來衡量兩個隨機變數的分佈之間的總體變化性，定義為 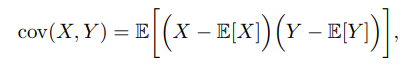協方差經常也用來衡量兩個隨機變數之間的線性相關性。如果兩個隨機變數的協方差為0，那麼稱這兩個隨機變數是線性不相關。兩個隨機變數之間沒有線性相關性，並非表示它們之間獨立的，可能存在某種非線性的函式關係。反之，如果X 與Y 是統計獨立的，那麼它們之間的協方差一定為0。 ### 隨機過程 隨機過程（stochastic process）是一組隨機變數Xt 的集合，其中t屬於一個索引（index）集合T 。索引集合T 可以定義在時間域或者空間域，但一般為時間域，以實數或正數表示。當t為實數時，隨機過程為連續隨機過程；當t為整數時，為離散隨機過程。日常生活中的很多例子包括股票的波動、語音訊號、身高的變化等都可以看作是隨機過程。常見的和時間相關的隨機過程模型包括貝努力過程、隨機遊走、馬爾可夫過程等。 **馬爾可夫過程** 指一個隨機過程在給定現在狀態及所有過去狀態情況下，其未來狀態的條件概率分佈僅依賴於當前狀態。 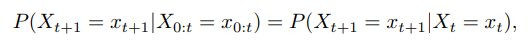其中X0:t 表示變數集合X0, X1, · · · , Xt，x0:t 為在狀態空間中的狀態序列。 **馬爾可夫鏈** 離散時間的馬爾可夫過程也稱為馬爾可夫鏈（Markov chain）。如果一個馬爾可夫鏈的條件概率 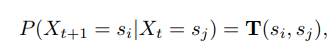馬爾可夫的使用可以看前面一篇寫的有意思的文章： [女朋友的心思你能猜得到嗎？——馬爾可夫鏈告訴你](https://mp.weixin.qq.com/s/2fyjOSSKXxvrCawTWR_2ow)隨機過程還有高斯過程，比較複雜，這裡就不詳細說明了。 ## 資訊理論 資訊理論（information theory）是數學、物理、統計、電腦科學等多個學科的交叉領域。資訊理論是由 Claude Shannon最早提出的，主要研究資訊的量化、儲存和通訊等方法。在機器學習相關領域，資訊理論也有著大量的應用。比如特徵抽取、統計推斷、自然語言處理等。 ### 自資訊和熵 在資訊理論中，熵用來衡量一個隨機事件的不確定性。假設對一個隨機變數X（取值集合為C概率分佈為`p(x), x ∈ C`）進行編碼，自資訊I(x)是變數X = x時的資訊量或編碼長度，定義為 I(x) = − log(p(x)), 那麼隨機變數X 的平均編碼長度，即熵定義為 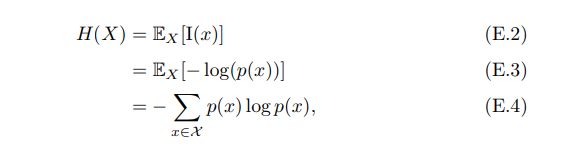其中當p(x) = 0時，我們定義0log0 = 0 熵是一個隨機變數的平均編碼長度，即自資訊的數學期望。熵越高，則隨機變數的資訊越多；熵越低，則資訊越少。如果變數X 當且僅當在x時`p(x) = 1`，則熵為0。也就是說，對於一個確定的資訊，其熵為0，資訊量也為0。如果其概率分佈為一個均勻分佈，則熵最大。假設一個隨機變數X 有三種可能值x1, x2, x3，不同概率分佈對應的熵如下：  **聯合熵和條件熵** 對於兩個離散隨機變數X 和Y ，假設X 取值集合為X；Y 取值集合為Y，其聯合概率分佈滿足為`p(x, y)`，則X 和Y 的聯合熵（Joint Entropy）為 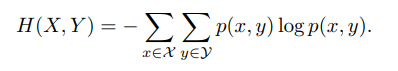X 和Y 的條件熵為 **互資訊** 互資訊（mutual information）是衡量已知一個變數時，另一個變數不確定性的減少程度。兩個離散隨機變數X 和Y 的互資訊定義為 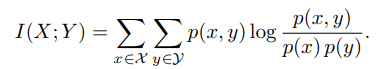交叉熵和散度 交叉熵 對應分佈為p(x)的隨機變數，熵H(p)表示其最優編碼長度。交叉熵是按照概率分佈q 的最優編碼對真實分佈為p的資訊進行編碼的長度，定義為 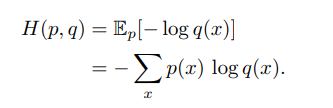在給定p的情況下，如果q 和p越接近，交叉熵越小；如果q 和p越遠，交叉熵就越大。