Redis 集合統計(HyperLogLog)
阿新 • • 發佈:2021-02-14
統計功能是一類極為常見的需求,比如下面這個場景:
為了決定某個功能是否在下個迭代版本中保留,產品會要求統計頁面在上新前後的 UV 作為決策依據。
簡單來說就是統計一天內,某個頁面的訪問使用者量,如果相同的使用者再次訪問,也只算記為一次訪問。 下面我們將從這個場景出發,討論如何選擇的合適的 Redis 資料結構實現統計功能。 # Redis與統計 ## 聚合統計 要完成這個統計任務,最直觀的方式是使用一個`SET`儲存頁面在某天的訪問使用者 ID,然後通過對集合求差`SDIFF`和求交`SINTER`完成統計: ```text # 2020-01-01 當日的 UV SADD page:uv:20200101 "Alice" "Bob" "Tom" "Jerry" # 2020-01-02 當日的 UV SADD page:uv:20200102 "Alice" "Bob" "Jerry" "Nancy" # 2020-01-02 新增使用者 SDIFFSTORE page:new:20200102 page:uv:20200102 page:uv:20200101 # 2020-01-02 新增使用者數量 SCARD page:new:20200102 # 2020-01-02 留存使用者 SINTERSTORE page:rem:20200102 page:uv:20200102 page:uv:20200101 # 2020-01-02 留存使用者數量 SCARD page:rem:20200102 ``` **優點:** - 操作直觀易理解,可以複用現有的資料集合 - 保留了使用者的訪問細節,可以做更細粒度的統計 **缺點:** - 記憶體開銷大,假設每個使用者ID長度均小於 44 位元組(使用 embstr 編碼),記錄 1 億使用者也至少需要 6G 的記憶體 - `SUNION`、`SINTER`、`SDIFF`計算複雜度高,大資料量情況下會導致 Redis 例項阻塞,可選的優化方式有: - 從叢集中選擇一個從庫專門負責聚合計算 - 把資料讀取到客戶端,在客戶端來完成聚合統計
只統計一個集合中不重複的元素個數,而並不關心集合元素內容的統計方式,我們將其稱為基數計數
理想情況下有 $k_{max} = log_2(n)$,反過來也可以通過 $k_{max}$ 來估計總的實驗次數 $n = 2^{k_{max}}$。 ### 處理極端情況 實際進行實驗時,極端情況總會出現,比如在第 1 次實驗時就連續丟擲了 10 次反面。 如果按照前面的公式進行估計,會認為已經進行了 1000 次實驗,這顯然與事實不符。 為了提高估計的準確性,可以同時使用 m 枚硬幣進行 **分組實驗**。 然後計算這 m 組實驗的平均值 $\hat{k}_{max} = \frac{\sum_{i=0}^{m}{k_{max}}}{m}$,此時能更準確的估計實際的實驗次數 $\hat{n}=2^{\hat{k}_{max}}$。 ## 基數統計 通過前面的分析,我們可以總結出以下經驗: > 可以通過二進位制串中首個 1 出現的位置 $k_{max}$ 來估計實際實驗發生的次數 $n$ `HyperLogLog`借鑑上述思想來統計集合中不重複元素的個數: - 使用 hash 函式集合中的每個元素對映為定長二進位制串 - 利用 **分組統計** 的方式提高準確性,將二進位制串分到 $m$ 個不同的桶`bucket`中分別統計 - 二進位制串的前 $log_2{m}$ 位用於計算該元素所屬的桶 - 剩餘二進位制位中,首個 1 出現的位元位記為 $k$,每個桶中的只儲存最大值 $k_{max}$ - 當需要估計集合中包含的元素個數時,使用公式 $\hat{n}=2^{\hat{k}_{max}}$ 計算即可
下面來看一個例子: 某個
使用該 HLL 統計 Alice,Bob,Tom,Jerry,Nancy 這 5 個使用者訪問頁後的 UV ```text 對映為二進位制串 分組 計算k | | | V V V +---------+ hash("Alice") => |01|101000| => bucket=1, k=1 +---------+ 分組統計 k_max +---------+ hash("Bob") => |11|010010| => bucket=3, k=2 +----------+----------+----------+----------+ +---------+ | bucket_0 | bucket_1 | bucket_2 | bucket_3 | +---------+ ==> +----------+----------+----------+----------+ hash("Tom") => |10|001000| => bucket=2, k=3 | k_max= 1 | k_max= 2 | k_max= 3 | k_max= 2 | +---------+ +----------+----------+----------+----------+ +---------+ hash("Jerry") => |00|111010| => bucket=0, k=1 +---------+ +---------+ hash("Nancy") => |01|010001| => bucket=1, k=2 +---------+ ``` 分組計數完成後,用之前的公式估計集合基數為 $2^{\hat{k}_{max}}= 2^{(\frac{1+2+3+2}{4})} = 4$。 ## 誤差分析 在 Redis 的實現中,對於一個輸入的字串,首先得到 64 位的 hash 值: - 前 14 位來定位桶的位置(共有16384個桶) - 後 50 位用作元素對應的二進位制串(用於更新首次出現 1 的位元位的最大值 $k_{max}$) 由於使用了 64 位輸出的 hash 函式,因此可以計數的集合的基數沒有實際限制。 `HyperLogLog`的標準誤差計算公式為 $\frac{1.04}{\sqrt{m}}$($m$ 為分組數量),據此計算 Redis 實現的標準誤差為 $0.81\%$。 下面這幅圖展示了統計誤差與基數大小的關係:
### 參考資料 - http://antirez.com/news/75 - https://www.yuque.com/abser/aboutm
簡單來說就是統計一天內,某個頁面的訪問使用者量,如果相同的使用者再次訪問,也只算記為一次訪問。 下面我們將從這個場景出發,討論如何選擇的合適的 Redis 資料結構實現統計功能。 # Redis與統計 ## 聚合統計 要完成這個統計任務,最直觀的方式是使用一個`SET`儲存頁面在某天的訪問使用者 ID,然後通過對集合求差`SDIFF`和求交`SINTER`完成統計: ```text # 2020-01-01 當日的 UV SADD page:uv:20200101 "Alice" "Bob" "Tom" "Jerry" # 2020-01-02 當日的 UV SADD page:uv:20200102 "Alice" "Bob" "Jerry" "Nancy" # 2020-01-02 新增使用者 SDIFFSTORE page:new:20200102 page:uv:20200102 page:uv:20200101 # 2020-01-02 新增使用者數量 SCARD page:new:20200102 # 2020-01-02 留存使用者 SINTERSTORE page:rem:20200102 page:uv:20200102 page:uv:20200101 # 2020-01-02 留存使用者數量 SCARD page:rem:20200102 ``` **優點:** - 操作直觀易理解,可以複用現有的資料集合 - 保留了使用者的訪問細節,可以做更細粒度的統計 **缺點:** - 記憶體開銷大,假設每個使用者ID長度均小於 44 位元組(使用 embstr 編碼),記錄 1 億使用者也至少需要 6G 的記憶體 - `SUNION`、`SINTER`、`SDIFF`計算複雜度高,大資料量情況下會導致 Redis 例項阻塞,可選的優化方式有: - 從叢集中選擇一個從庫專門負責聚合計算 - 把資料讀取到客戶端,在客戶端來完成聚合統計
只統計一個集合中不重複的元素個數,而並不關心集合元素內容的統計方式,我們將其稱為基數計數
cardinality counting
針對這一特定的統計場景,Redis 提供了`HyperLogLog`型別支援基數統計:
```text
# 2020-01-01 當日的 UV
PFADD page:uv:20200101 "Alice" "Bob" "Tom" "Jerry"
PFCOUNT page:uv:20200101
# 2020-01-02 當日的 UV
PFADD page:uv:20200102 "Alice" "Bob" "Tom" "Jerry" "Nancy"
PFCOUNT page:uv:20200102
# 2020-01-01 與 2020-01-02 的 UV 總和
PFMERGE page:uv:union page:uv:20200101 page:uv:20200102
PFCOUNT page:uv:union
```
**優點:**
`HyperLogLog`計算基數所需的空間是固定的。只需要 12KB 記憶體就可以計算接近 $2^{64}$ 個元素的基數。
**缺點:**
`HyperLogLog`的統計是基於概率完成的,其統計結果是有一定誤差。不適用於精確統計的場景。
# HyperLogLog 解析
## 概率估計
`HyperLogLog`是一種基於概率的統計方式,該如何理解?
我們來做一個實驗:**不停地拋一個均勻的雙面硬幣,直到結果是正面為止**。
用 0 和 1 分別表示正面與反面,則實驗結果可以表示為如下二進位制串:
```text
+-+
第 1 次拋到正面 |1|
+-+
+--+
第 2 次拋到正面 |01|
+--+
+---+
第 3 次拋到正面 |001|
+---+
+---------+
第 k 次拋到正面 |000...001| (總共 k-1 個 0)
+---------+
```
由於每次拋硬幣得到正面的概率均為$\frac{1}{2}$,因此實驗在第 k 次結束的可能性為 $(\frac{1}{2})^k$(二進位制串中首個 1 出現在第 k 位的概率)。理想情況下有 $k_{max} = log_2(n)$,反過來也可以通過 $k_{max}$ 來估計總的實驗次數 $n = 2^{k_{max}}$。 ### 處理極端情況 實際進行實驗時,極端情況總會出現,比如在第 1 次實驗時就連續丟擲了 10 次反面。 如果按照前面的公式進行估計,會認為已經進行了 1000 次實驗,這顯然與事實不符。 為了提高估計的準確性,可以同時使用 m 枚硬幣進行 **分組實驗**。 然後計算這 m 組實驗的平均值 $\hat{k}_{max} = \frac{\sum_{i=0}^{m}{k_{max}}}{m}$,此時能更準確的估計實際的實驗次數 $\hat{n}=2^{\hat{k}_{max}}$。 ## 基數統計 通過前面的分析,我們可以總結出以下經驗: > 可以通過二進位制串中首個 1 出現的位置 $k_{max}$ 來估計實際實驗發生的次數 $n$ `HyperLogLog`借鑑上述思想來統計集合中不重複元素的個數: - 使用 hash 函式集合中的每個元素對映為定長二進位制串 - 利用 **分組統計** 的方式提高準確性,將二進位制串分到 $m$ 個不同的桶`bucket`中分別統計 - 二進位制串的前 $log_2{m}$ 位用於計算該元素所屬的桶 - 剩餘二進位制位中,首個 1 出現的位元位記為 $k$,每個桶中的只儲存最大值 $k_{max}$ - 當需要估計集合中包含的元素個數時,使用公式 $\hat{n}=2^{\hat{k}_{max}}$ 計算即可
下面來看一個例子: 某個
HyperLogLog實現,使用8bit 輸出的 hash 函式並以 4 個桶進行分組統計使用該 HLL 統計 Alice,Bob,Tom,Jerry,Nancy 這 5 個使用者訪問頁後的 UV ```text 對映為二進位制串 分組 計算k | | | V V V +---------+ hash("Alice") => |01|101000| => bucket=1, k=1 +---------+ 分組統計 k_max +---------+ hash("Bob") => |11|010010| => bucket=3, k=2 +----------+----------+----------+----------+ +---------+ | bucket_0 | bucket_1 | bucket_2 | bucket_3 | +---------+ ==> +----------+----------+----------+----------+ hash("Tom") => |10|001000| => bucket=2, k=3 | k_max= 1 | k_max= 2 | k_max= 3 | k_max= 2 | +---------+ +----------+----------+----------+----------+ +---------+ hash("Jerry") => |00|111010| => bucket=0, k=1 +---------+ +---------+ hash("Nancy") => |01|010001| => bucket=1, k=2 +---------+ ``` 分組計數完成後,用之前的公式估計集合基數為 $2^{\hat{k}_{max}}= 2^{(\frac{1+2+3+2}{4})} = 4$。 ## 誤差分析 在 Redis 的實現中,對於一個輸入的字串,首先得到 64 位的 hash 值: - 前 14 位來定位桶的位置(共有16384個桶) - 後 50 位用作元素對應的二進位制串(用於更新首次出現 1 的位元位的最大值 $k_{max}$) 由於使用了 64 位輸出的 hash 函式,因此可以計數的集合的基數沒有實際限制。 `HyperLogLog`的標準誤差計算公式為 $\frac{1.04}{\sqrt{m}}$($m$ 為分組數量),據此計算 Redis 實現的標準誤差為 $0.81\%$。 下面這幅圖展示了統計誤差與基數大小的關係:
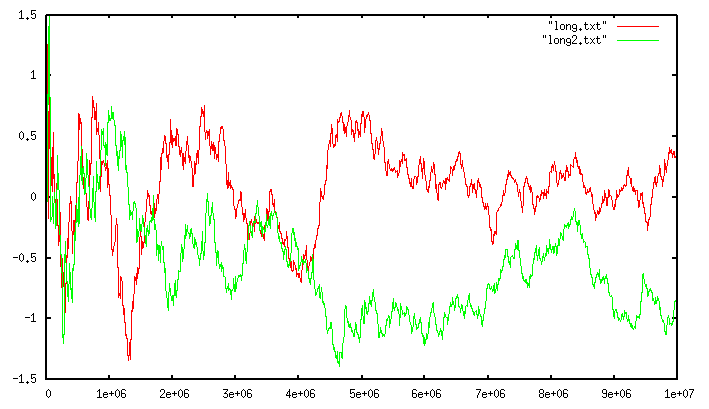
### 參考資料 - http://antirez.com/news/75 - https://www.yuque.com/abser/aboutm
