Deep Unfolding Network for Image Super-Resolution 論文解讀
阿新 • • 發佈:2021-03-01
# Introduction
超分是一個在 low level CV 領域中經典的病態問題,比如增強影象視覺質量、改善其他 high level 視覺任務的表現。Zhang Kai 老師這篇文章在我看到的超分文章裡面是比較驚豔我的一篇,首先他指出基於學習(learning-based)的方法表現出高效,且比傳統方法更有效的特點。可是比起基於模型(model-based)的方法可以通過統一的最大後驗框架來解決不同的 scale factors、blur kernels 和 noise levels 的問題,基於學習的方法看起來反而有些缺乏靈活性了。而文章提出了一種可以端到端的可訓練的迭代模型,針對基於模型和基於學習的方法搭起了橋樑。
# Unfolding optimization
根據最大後驗(MAP)框架,HR 影象可以通過最小化以下能量函式得到:
$$
E(x)=\frac{1}{2\sigma^2}\lVert y-(x \otimes k)\downarrow_s \rVert^2 + \lambda \Phi(x)
$$
式中前面一項可以看作基於模型方法來進行超分,文章中稱之為資料項。後面一項也稱為先驗項,可以理解為圖片中的一些噪聲。為了使其能夠不斷迭代,文章中使用了半二方分裂法(HQS),原因有二:簡潔性和快速收斂。HQS 常常解決上式優化問題引入輔助變數 z:
$$
E_{\mu}(x)=\frac{1}{2\sigma^2}\lVert y-(z \otimes k)\downarrow_s \rVert^2 + \lambda \Phi(x) + \frac{\mu}{2}\lVert z-x \rVert^2
$$
其中 $\mu$ 可以看作懲罰引數,上式可以不斷迭代迴圈求解子問題來得到 x 和 z:
$$
\begin{cases}
z_k &= \mathrm{argmin}_z \lVert y-(z \otimes k)\downarrow_s \rVert^2 + \mu \sigma^2 \lVert z-x_{k-1} \rVert^2 \tag{#}\\
x_k &= \mathrm{argmin}_x \frac{\mu}{2} \lVert z_k - x \rVert^2 + \lambda \Phi(x)
\end{cases}
$$
顯然第一式的 $\mu$ 應該足夠大,可以理解為 $\lVert z-x_{k-1} \rVert$ 的權重,權重越大時,z 和 x 才會越接近。顯然之前提到的資料項和先驗項分別由上面二式進行求得。對於第一式,文中在圓周邊界條件下卷積可以被求解的情況下使用了 FFT,根據論文Fast single image super-resolution using a new analytical solution for ℓ2-ℓ2 problems 該式有封閉形式的解:
$$
z_k = \mathcal{F}^{-1}\bigg(\frac{1}{\alpha_k}\Big(d-\overline{\mathcal{F}(k)} \odot_{s} \frac{(\mathcal{F}(k)d)\Downarrow_s}{(\overline{\mathcal{F}(k)}\mathcal{F}(k))\Downarrow_s+\alpha_k}\Big)\bigg)
$$
其中 $d = \overline{\mathcal{F}(k)}\mathcal{F}(y \uparrow_s) + \alpha_k \mathcal{F}(x_{k-1}),\alpha_k \triangleq \mu_k \sigma^2$,當上式的 $s=1$ 時,相當於完全針對的 deblurring 問題。對於 # 式中的第二式實際上是一個噪聲水平為 $\beta_k \triangleq \sqrt{\lambda / \mu_k}$ 的去噪問題。
# Deep unfolding network
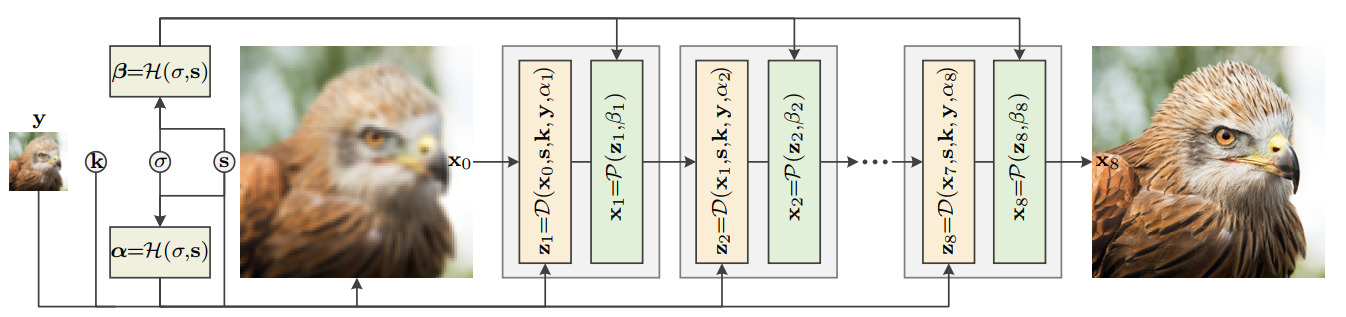
如上圖所示,Unfolding SuperResolution Network(USRNet) 主要的輸入為低解析度圖 $y$,模糊核 $k$,噪聲水平 $\sigma$,以及影象縮放比例 $s$。整個模型還有三個模組 $\mathcal{D}$、$\mathcal{P}$ 以及 $\mathcal{H}$,分別的功能是進行基於模型的超分、基於學習的去噪以及超引數的預測。整個流程為:
♠ 將預設的噪聲水平 $\sigma$ 與縮放倍數 $s$ 作為 $H$ module 的輸入,對超引數 $\alpha$ 和 $beta$ 進行預測;
♣ 將 $y$ 使用簡單的上取樣到最後的輸出 $x_{last}$ 一樣的尺寸,作為迭代最初始的輸入 $x_0$,最後將 $x_0,s,k,y,\alpha$ 作為 $\mathcal{D}$ module 的輸入。得到 $z$ 一次迭代的解;
♥ 將 $\mathcal{D}$ module 得到的解以及預測的超引數 $beta$ 作為輸入送入 $\mathcal{P}$ module 得到一次迭代的 $x$;
♦ 最後將得到的 $x$ 送入下一輪迭代。
## Data module $\mathcal{H}$
$\mathcal{H}$ 模組其實就是將預設的噪聲水平和需要超分的倍數作為輸入,其實現是深度學習的方式,使用簡單的幾層網路實現,並預測接下來每一次迭代需要的超引數 $\alpha_1, \alpha_2, \ldots$,$\beta_1, \beta_2, \ldots$。
## Data module $\mathcal{D}$
$\mathcal{D}$ 模組被稱之為資料模組,它的作用實際上是用來實現 (#) 式的第一式的。其實它就是一張圖片在一次迭代中的超分後的解析解。式中的前面一項是使用基於模型的方法對影象進行超分辨的重建,這種基於模型的方法可以對任意 scale、任意模糊核進行超分辨重建,後面一項可以看作正則化項,用於 x 與 z 進行逼近。
## Prior module $\mathcal{P}$
$\mathcal{P}$ 模組被稱之為先驗模組,也就是 (#) 式的第二式。常常這一式被看作去噪的過程,因為噪聲可以用先驗知識預設,因而被稱之為先驗項。文章採用基於學習(也就是深度學習)的方法來進行求解得到去噪後的影象 $x$。文章使用的結構叫做 ResUNet,顧名思義是將 residual blocks 整合進入了 U-Net,網路結構比較簡單,具體可以檢視[程式碼](https://github.com/cszn/KAIR/blob/master/models/network_usrnet.py)。
# 關於訓練
USRNet 關於[訓練資料]("https://github.com/cszn/KAIR/blob/master/data/dataset_usrnet.py")的製作,使用隨機的高斯核與運動模糊核來作為卷積的模糊核,再經過下采樣並新增不同水平的白噪聲來製作每張 HR 的 LR,並且每個 batch 從 $s={1,2,3,4}$ 中選擇一個作為下采樣的倍數,並且也作為模型關於這個 batch 進行超分 scale 的輸入。這樣一來使得 USRNet 可以對任意 scale、任意模糊核的情況具有較強的泛化性。
# 關於 USRNet 的泛化性
雖然 USRNet 是在模糊核為 $25*25$ 的情況下進行訓練的,然而再測試超分 $67*67$,$70*70$ 時,也表現出不錯的效果。

# 一些總結
ZhangKai 這篇文章使用了 HQS 來把優化問題分裂為可迭代的兩個子問題,使得基於模型核基於學習進行結合成為了可能。基於模型超分讓 USRNet 更加靈活,可以針對不同的模糊核與上取樣尺寸的情況進行超分,而基於學習去噪可以不用預定義去噪器,可以儘可能去擬合各種可能情況的噪聲。
但是我認為其任有改進的地方:
♠ 進行實際應用的時候,需要對每張圖片指定模糊核,然而這個模糊核的選定是否符合真實情況比較影響後面超分的效果。因此,是否考慮進行設計一個對 kernel 進行預測的網路
♣ 每張圖需要指定噪聲水平,這一點也沒有做到自適應
[程式碼位置]("https://github.com/csz


