>微信搜一搜：【bigsai】 獲取更多肝貨知識 > 春風十里，感謝有你 ## 前言 Hello，大家好，我是bigsai，long time no see！在刷題和麵試過程中，我們經常遇到一些排列組合類的問題，而全排列、組合、子集等問題更是非常經典問題。本篇文章就帶你徹底搞懂全排列！ **求全排列？** 全排列即：n個元素取n個元素(所有元素)的所有**排列組合情況**。 **求組合？** 組合即：n個元素取m個元素的所有**組合情況(非排列)**。 **求子集？** 子集即：n個元素的所有子集(**所有可能的組合情況**)。 總的來說全排列數值個數是所有元素，不同的是排列順序；而組合是選取固定個數的組合情況(不看排列)；子集是對組合拓展，所有可能的組合情況(同不考慮排列)。 當然，這三種問題，有相似之處又略有所不同，我們接觸到的全排列可能更多，所以你可以把組合和子集問題認為是全排列的拓展變形。且問題可能會遇到**待處理字元是否有重複**的情況。採取不同的策略去去重也是相當關鍵和重要的！在各個問題的具體求解上方法可能不少，在全排列上最流行的就是**鄰里互換法**和**回溯法**，而其他的組合和子集問題是經典回溯問題。而本篇最重要和基礎的就是要掌握這兩種方法實現的**無重複全排列**，其他的都是基於這個進行變換和拓展。 ## 全排列問題 全排列，元素總數為最大，不同是**排列的順序**。 ### 無重複序列的全排列 這個問題剛好在[力扣46題](https://leetcode-cn.com/problems/permutations/)是原題的，大家學完可以去a試試。 問題描述： > 給定一個 **沒有重複** 數字的序列，返回其所有可能的全排列。 示例： ``` 輸入: [1,2,3] 輸出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] ``` **回溯法實現無重複全排列** 回溯演算法用來解決搜尋問題，而全排列剛好也是一種搜尋問題，先回顧一下什麼是回溯演算法： > 回溯演算法實際上一個類似列舉的搜尋嘗試過程，主要是在搜尋嘗試過程中尋找問題的解，當發現已不滿足求解條件時，就“回溯”返回，嘗試別的路徑. 而全排列剛好可以使用試探的方法去列舉所有中可能性。一個長度為n的序列或者集合。它的所有排列組合的可能性共有`n！`種。具體的試探策略如下： 1. 從待選集合中選取第一個元素(共有n種情況)，並標記該元素已經被使用不能再使用。 2. 在步驟1的基礎上進行遞迴到下一層，從剩餘n-1個元素中按照1的方法找到一個元素並標記，繼續向下遞迴。 3. 當所有元素被標記後，順序收集被標記的元素儲存到結果中，當前層遞迴結束，回到上一層(同時將當前層標記的元素清除標記)。這樣一直執行到最後。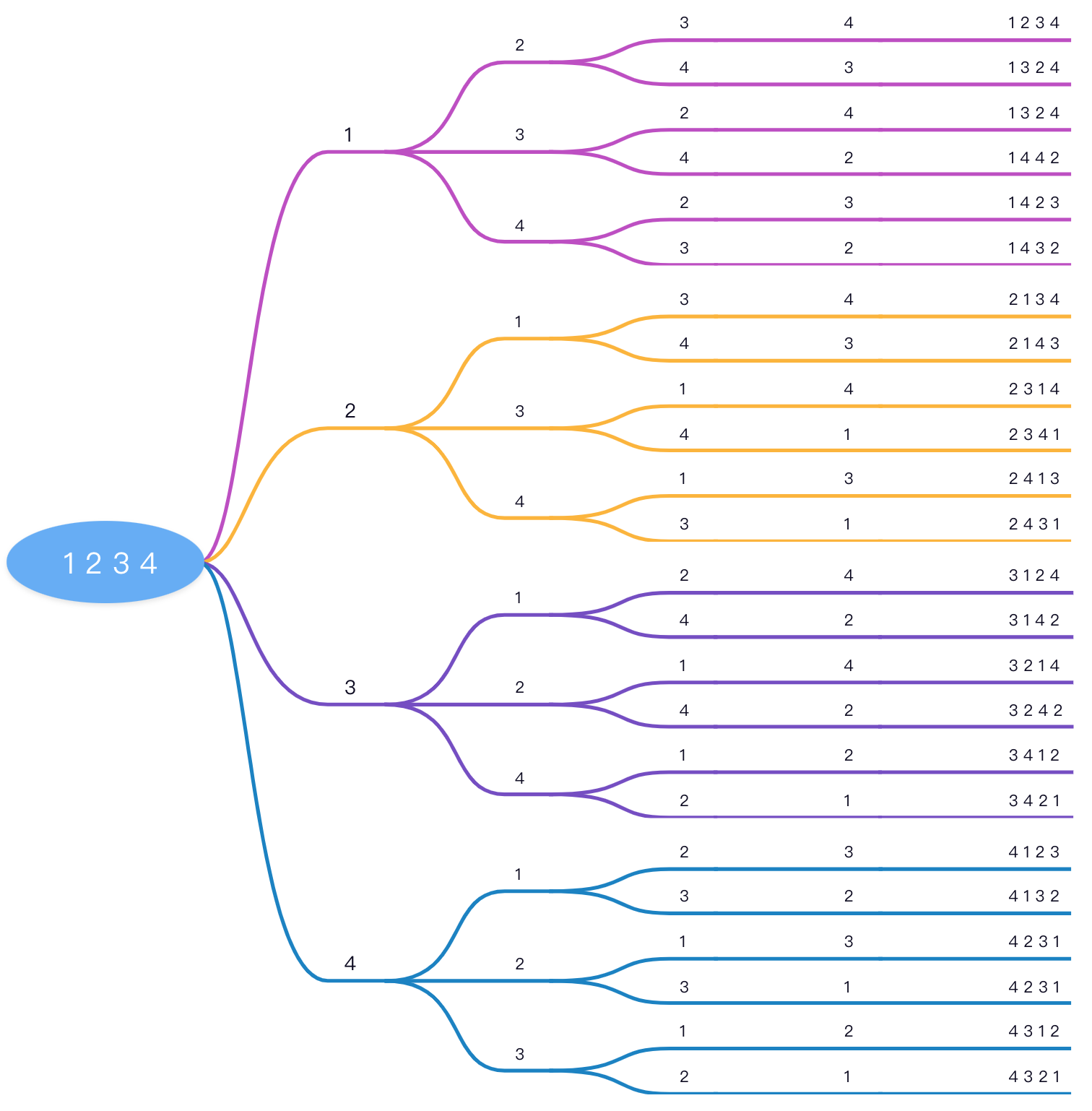 回溯的流程如果從虛擬碼流程大致為這樣： ``` 遞迴函式： 如果集合所有元素被標記： 將臨時儲存新增到結果集中 否則： 從集合中未標記的元素中選取一個儲存到臨時集合中 標記該元素被使用 下一層遞迴函式 (這層遞迴結束)標記該元素未被使用 ``` 如果用序列 **1 2 3 4**來表示這麼回溯的一個過程，可以用這張圖來顯示：  用程式碼來實現思路也是比較多的，需要一個List去儲存臨時結果是很有必要的，但是對於原集合我們標記也有兩種處理思路，第一種是使用List儲存集合，使用過就移除然後遞迴下一層，遞迴完畢後再新增到原來位置。另一種思路就是使用固定陣列儲存，使用過對應位置使用一個boolean陣列對應位置標記一下，遞迴結束後再還原。因為List頻繁查詢插入刪除效率一般比較低，所以我們一般**使用一個boolean陣列去標記該位置元素是否被使用**。 具體實現的程式碼為： ```j