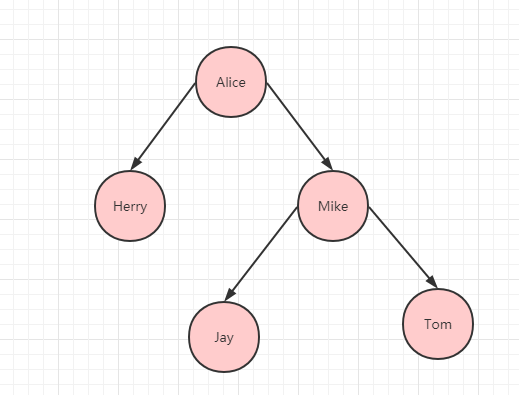
3 月 12 號，是全國的重大節日：植樹節，記得小時候就跟隨老師一起植過樹。現在參加工作了，雖然沒有植過樹，但是學到過很多樹的結構，比如二叉樹、B+ 樹，紅黑樹。每次面試必問，恰逢植樹節，這裡給大家做個二叉樹的總結，也方便自己複習。 ## 大白話講解二叉樹 比如現在有個陣列，存放了很多使用者的名字，需要從這個陣列中找到包含指定的使用者名稱，最快的方式是什麼？ 我們會想到二分查詢，雖然這種方式很快，但要達到最快還需要有個條件：陣列有序。 如果我們能把插入使用者名稱的時候直接給他排序，那最後的結構就是有序結構。 因此有人設計了一種資料結構：二叉查詢樹，也叫做二叉樹。 如下圖所示：這是一種二叉樹結構。  根據上文中的例子的，假定 Herry 在最上面，下面有 Alice，Mike，Ivy，Tom，從左到右，從上到下來看的話，最後的排序是： Alice->Herry->Ivy->Mike->Tom，確實是按照字母順序排的。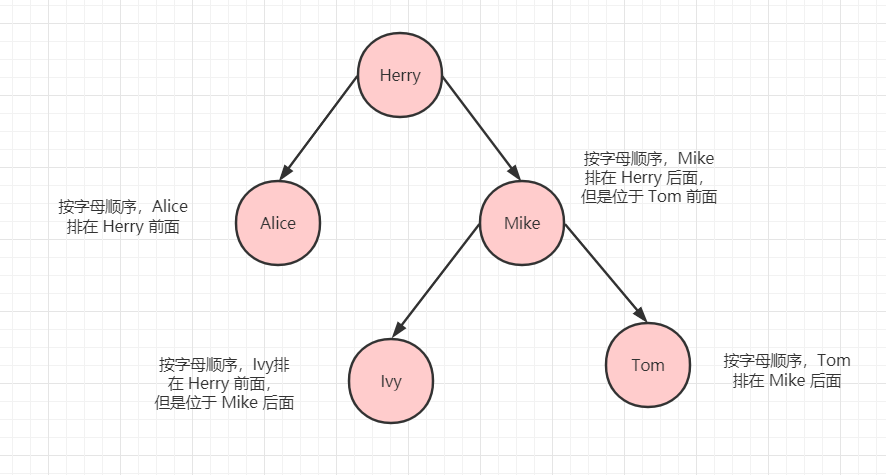  其中有四個術語需要說明：節點、左節點、右節點、根節點。 其中每個紅色圓球都算一個節點，節點左下邊相連線的節點叫做左節點，而右邊相連的叫做右節點。比如 Alice 被稱作 Herry 節點的左節點，Mike 被稱作 Herry 的右節點。而根節點只會有一個，屬於最上面的節點，上圖中的 Herry 就是根節點。 對於其中每個節點，左子節點的值都比它小，而右子節點的值都比它大。比如 Alice < Herry < Mike。 假設現在我們想要查詢 Ivy，首先檢查根節點，發現比 Herry 大，所以往下繼續找，找到了根節點的右節點 Mike，再繼續找，比 Mike 小，所以找 Mike 的左節點，正好找到 Ivy。 二叉查詢樹中查詢節點時，平均執行時間是 O(logn)，最糟糕的情況下所需時間為 O(n); 而在有序陣列中查詢時，及時最糟糕的情況，二分查詢最多也是 O(logn)，所以你可能會覺得，二分查詢比二叉查詢要快很多。但是二叉查詢樹的插入和刪除操作的速度是要快很多的。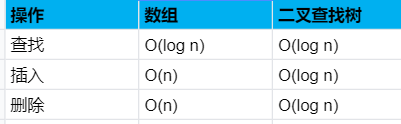這裡我們做一個對比：  但是二叉樹也有缺點： - 不能隨機訪問。比如想要查詢第 10 個元素，是不能返回第十個元素的，但是陣列就可以通過下標索引找到。 - 二叉樹存在不平衡的情況，比如以根節點為中間的界限，發現右邊的節點數遠超左邊的節點數，那麼左右不平衡，查詢的效率就很低了。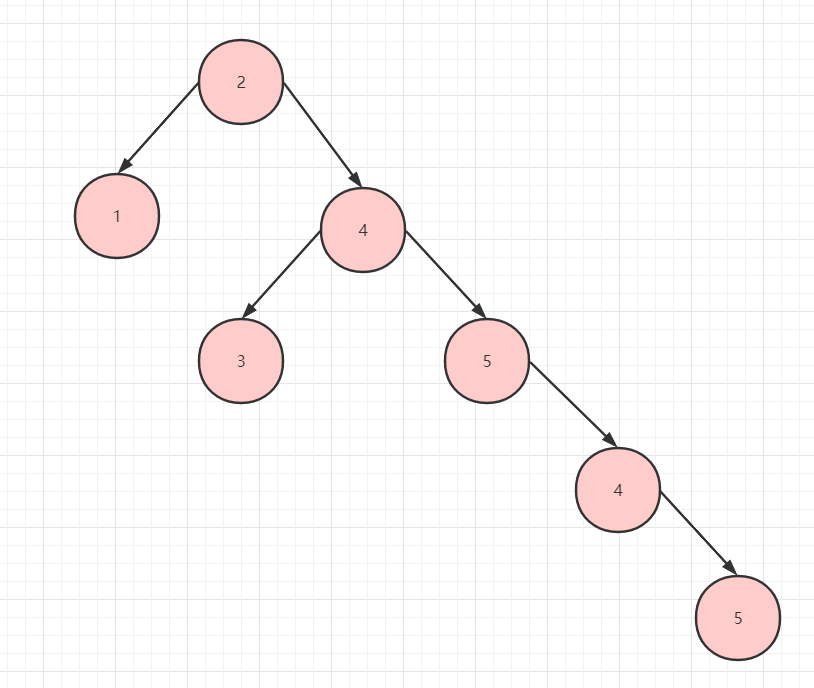如下圖所示：  那有沒有平衡的二叉樹呢？當然有，那就是紅黑樹，限於篇幅和側重點，這個放到下篇再講吧 ## 二叉樹中的含義 ### 二叉樹定義 大白話說二叉樹就是每個節點只能有兩顆子樹，且有左右之分。 來看看專業定義：**二叉樹**是 n(n>=0 ) 個結點的有限集合，該集合或者為空集（稱為空二叉樹），或者由一個根結點和兩棵互不相交的、分別稱為根結點的左子樹和右子樹組成。 ### 二叉樹有 5 種形態 - 空二叉樹。  - 只有一個根節點的二叉樹。  - 只有左子樹  - 只有右子樹。  - 完全二叉樹。  ### 節點的度 定義：節點擁有的子樹數目稱為節點的`度`。 我們來看下圖就一目樂然了。  比如節點 B 的度為 2，節點 E 的度 為 1. 而樹的度就是所有節點的度的最大值，也就是 2。 ### 節點層次 如下圖所示：根節點為第一層，依次類推。  ### 二叉樹的特點 - 每個節點最多有顆子樹，所以二叉樹中不存在度大於 2 的節點。 - 左右子樹是有順序的，次序不能任意顛倒。 - 即使某個節點只有一顆子樹，也是需要區分它是左子樹還是右子樹。 ## 二叉樹的遍歷 二叉樹的遍歷：從二叉樹的根節點出發，按照某種次序依次訪問二叉樹中的所有節點，使得每個節點都能被訪問一次，且僅被訪問一次。 二叉樹的訪問次序可以分為四種： - 前序遍歷。 - 中序遍歷。 - 後續遍歷。 - 層序遍歷。 **前序遍歷**：通俗的說就是從二叉樹的根結點出發，當第一次到達結點時就輸出結點資料，按照先向左在向右的方向訪問。 **中序遍歷**：就是從二叉樹的根結點出發，當第二次到達結點時就輸出結點資料，按照先向左再向右的方向訪問。 **後序遍歷**：就是從二叉樹的根結點出發，當第三次到達結點時就輸出結點資料，按照先向左再向右的方向訪問。 **層次遍歷**：就是按照樹的層次自上而下的遍歷二叉樹。  按照前序遍歷的結果就是 BADCE。 按照中序遍歷的結果就是 ABCDE。 按照後續遍歷的結果就是 ACEDB。 按照層次遍歷的結果就是 BADCE。 巨人的肩膀： 《演算法圖解》 https://www.jianshu.com/p/bf73c