隨機事件x的資訊量：
h(x) = − log 2 p(x)
隨機變數的熵：
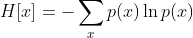
熵的單位
單位取決於定義用到對數的底。當b = 2，熵的單位是bit；當b = e，熵的單位是nat；而當b = 10,熵的單位是 Hart。
熵的取值範圍：
0<=H[X]<=log(n) ， n是事件個數

熵的特性：
連續性
該量度應連續，概率值小幅變化只能引起熵的微小變化。
對稱性
符號xi重新排序後，該量度應不變。
極值性
當所有符號等可能出現的情況下，熵達到最大值（所有可能的事件等概率時不確定性最高）。

增減一概率為零的事件不改變熵。
微分熵：

推導：

對概率密度函式採取微元法

可以看到，微元法直接計算的微分熵值是無窮大，連續隨機變數的熵是無窮大的，無法計算了

取前面一部分作為微分熵：

這樣定義的目的：
>嫡差具有資訊度量的意義
>與離散信源的嫡在形式上統一

因為前面已經減少了一個正無窮大，所以有負值了。

夏農熵的變型和拓展

聯合熵(joint entropy)

就是二維隨機變數直接拓展過來的。

條件熵(conditional entropy)

可理解為給定X的值前提下隨機變數Y的隨機性的量。

條件熵 H(Y|X)定義為 X 給定條件下 Y 的條件概率分佈的熵對 X 的數學期望：

條件熵 H(Y|X)相當於聯合熵 H(X,Y)減去單獨的熵 H(X)，即H(Y|X)=H(X,Y)−H(X)，證明如下：

舉個例子，比如環境溫度是低還是高，和我穿短袖還是外套這兩個事件可以組成聯合概率分佈 H(X,Y)，因為兩個事件加起來的資訊量肯定是大於單一事件的資訊量的。假設 H(X)對應著今天環境溫度的資訊量，由於今天環境溫度和今天我穿什麼衣服這兩個事件並不是獨立分佈的，所以在已知今天環境溫度的情況下，我穿什麼衣服的資訊量或者說不確定性是被減少了。當已知 H(X) 這個資訊量的時候，H(X,Y) 剩下的資訊量就是條件熵：H(Y|X)=H(X,Y)−H(X)

因此，可以這樣理解，描述 X 和 Y 所需的資訊是描述 X 自己所需的資訊,加上給定 X的條件下具體化 Y 所需的額外資訊。

互資訊(mutual information)

如果 (X, Y) ~ p(x, y), X, Y 之間的互資訊 I(X; Y)定義為:

Note: 互資訊 I (X; Y)取值為非負。當X、Y相互獨立時，I(X,Y)最小為0。

互資訊實際上是更廣泛的相對熵的特殊情形

如果變數不是獨立的,那麼我們可以通過考察聯合概率分佈與邊緣概率分佈乘積之間的 Kullback-Leibler 散度來判斷它們是否“接近”於相互獨立。此時, Kullback-Leibler 散度為

這被稱為變數 x 和變數 y 之間的互資訊( mutual information )。根據 Kullback-Leibler 散度的性質,我們看到 I[x, y] ≥ 0 ,當且僅當 x 和 y 相互獨立時等號成立。

使用概率的加和規則和乘積規則,我們看到互資訊和條件熵之間的關係為

可以把互資訊看成由於知道 y 值而造成的 x 的不確定性的減小(反之亦然)（即Y的值透露了多少關於X 的資訊量）。就是X,Y的公共資訊量咯。

點互資訊：

定義：

點互資訊使用者衡量兩個變數的相關性。是從互資訊中引申出來的，形式上可以看做互資訊中一個點的資訊量，和熵中一個點的資訊量類似，熵點的資訊量加權累積的得到熵，點互資訊加權累加就是互資訊了。還可以看做知道y時，x的條件概率p(x|y)與原來的概率p(x)比值求log得到。想一想，衡量兩個變數的相關性似乎可以直接用p(x,y)大小來衡量，這樣行嗎，由於如果x很多，就算x和y一起出現比較少，p(x,y)也大，而如果x,y很少，但是卻經常一起出現，p(x,y)還是很小的，就不對了，所以p(x,)不能作為衡量標準，那麼在下面處於p(x),p(y)就可以了。就可以看成在x,y的概率條件下，一起出現的概率。然後log，得到資訊量。

取值範圍：

可以為負，最大為-logp(x)或者-logp(y)

和互資訊很多性質類似，比如

h(x)即資訊量.

互資訊、條件熵與聯合熵的區別與聯絡

venn圖表示關係