CodeForces #869 Div2
CodeForces #869 Div2
- A. The Artful Expedient
- B. The Eternal Immortality
- C. The Intriguing Obsession(神仙組合數)
- D. The Overdosing Ubiquity
A. The Artful Expedient
time limit per test1 second memory limit per test256 megabytes inputstandard input outputstandard output Rock... Paper!After Karen have found the deterministic winning (losing?) strategy for rock-paper-scissors, her brother, Koyomi, comes up with a new game as a substitute. The game works as follows.
A positive integer n is decided first. Both Koyomi and Karen independently choose n distinct positive integers, denoted by x1, x2, …, xn and y1, y2, …, yn respectively. They reveal their sequences, and repeat until all of 2n integers become distinct, which is the only final state to be kept and considered.
Then they count the number of ordered pairs (i, j) (1 ≤ i, j ≤ n) such that the value xi xor yj equals to one of the 2n integers. Here xor means the bitwise exclusive or operation on two integers, and is denoted by operators ^ and/or xor in most programming languages.
Karen claims a win if the number of such pairs is even, and Koyomi does otherwise. And you’re here to help determine the winner of their latest game.
Input
The first line of input contains a positive integer n (1 ≤ n ≤ 2 000) — the length of both sequences.
The second line contains n space-separated integers x1, x2, …, xn (1 ≤ xi ≤ 2·106) — the integers finally chosen by Koyomi.
The third line contains n space-separated integers y1, y2, …, yn (1 ≤ yi ≤ 2·106) — the integers finally chosen by Karen.
Input guarantees that the given 2n integers are pairwise distinct, that is, no pair (i, j) (1 ≤ i, j ≤ n) exists such that one of the following holds: xi = yj; i ≠ j and xi = xj; i ≠ j and yi = yj.
Output
Output one line — the name of the winner, that is, “Koyomi” or “Karen” (without quotes). Please be aware of the capitalization.
Examples
inputCopy
3
1 2 3
4 5 6
outputCopy
Karen
inputCopy
5
2 4 6 8 10
9 7 5 3 1
outputCopy
Karen
Note
In the first example, there are 6 pairs satisfying the constraint: (1, 1), (1, 2), (2, 1), (2, 3), (3, 2) and (3, 3). Thus, Karen wins since 6 is an even number.
In the second example, there are 16 such pairs, and Karen wins again.
題意:給你長度都為n的序列,xn和yn,問你存在多少組pair(i.j),即x[i]^y[j]是這2n個元素裡出現過的,如果存在偶陣列,則Karen獲勝,否則Koyomi獲勝
解析:存一下之前的數,2000個數直接列舉算一下,判斷一下之前是否出現過,算一下次數,2000*2000的複雜度直接暴力
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
#define Maxn 2005
int a[Maxn],b[Maxn];
bool vis[10000005];
int main(int argc,char *argv[]) {
int n; scanf("%d",&n);
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
vis[a[i]] = 1;
}
for(int i=1; i<=n; i++) {
scanf("%d",&b[i]);
vis[b[i]] = 1;
}
int num = 0;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++) {
if(vis[a[i] ^ b[j]]) num++;
}
if(num & 1) cout << "Koyomi";
else cout << "Karen";
return 0;
}
然而有一種非常牛逼的做法,假如a^b = c, 則a^c = a b^a = b;這是一個迴圈,如果輸入中有出現,那必定成為一個 環 ,出現的次數為偶數,無論怎麼樣都是Karen贏。
所以直接輸出“Karen”當然也是ok的。
B. The Eternal Immortality
Even if the world is full of counterfeits, I still regard it as wonderful.
Pile up herbs and incense, and arise again from the flames and ashes of its predecessor — as is known to many, the phoenix does it like this.
The phoenix has a rather long lifespan, and reincarnates itself once every a! years. Here a! denotes the factorial of integer a, that is, a! = 1 × 2 × … × a. Specifically, 0! = 1.
Koyomi doesn’t care much about this, but before he gets into another mess with oddities, he is interested in the number of times the phoenix will reincarnate in a timespan of b! years, that is, . Note that when b ≥ a this value is always integer.
As the answer can be quite large, it would be enough for Koyomi just to know the last digit of the answer in decimal representation. And you’re here to provide Koyomi with this knowledge.
Input
The first and only line of input contains two space-separated integers a and b (0 ≤ a ≤ b ≤ 1018).
Output
Output one line containing a single decimal digit — the last digit of the value that interests Koyomi.
Examples
Input
2 4
Output
2
Input
0 10
Output
0
Input
107 109
Output
2

題目大意: 給出a,b 問b的階乘除以a的階乘的最後一位。 沒啥好寫的,直接暴力
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int main(int argc,char* argv[]) {
long long a,b,ans = 1;
cin >> a >> b;
if(b - a >= 10) cout << 0;
else {
for(long long i=a+1; i<=b; i++) {
ans = (ans * (i % 10)) % 10;
if(ans == 0) break;
}
cout << ans;
}
return 0;
}
// i 沒開long long掛了一遍
C. The Intriguing Obsession(神仙組合數)
貼個程式碼先,別的東西以後再寫
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long LL;
const LL Maxn = 5009;
const LL Mod = 998244353;
LL a, b,c,C[Maxn][Maxn],ans = 1,fac[Maxn];
void init() {
C[0][0] = 1;fac[0] = 1;
for(int i=1; i<=5000; i++) {
C[i][0] = 1,fac[i] = fac[i - 1] * (LL) i % Mod;
for(int j=1; j<=i; j++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % Mod;
}
}
void calc(LL a,LL b) {
LL minn = min(a,b),temp = 0;
for(int i=0; i<=minn; i++)
temp = (temp + C[a][i] * C[b][i] % Mod * fac[i] % Mod) % Mod;
ans = ans * temp % Mod;
}
int main(int argc,char* argv[]) {
cin >> a >> b >> c;
init();
calc(a,b); calc(a,c); calc(b,c);
cout << ans;
return 0;
}
D. The Overdosing Ubiquity
**笑死,想補題,根本看不懂** **題目描述:**有一棵有n個點的完全二叉樹,在這棵樹上新增m條邊,問這棵樹有多少條簡單路徑。 **solution** 一開始以為是列舉經過哪些新增上去的邊,然後算貢獻,但發現這樣會有很多複雜的情況。 有很多複雜的情況?恩。。。不如暴力搜尋。 顯然,添加了邊後,樹上就會出現環,但其實樹上還有很多點都是隻有單個入口的,而這些點都可以進行壓縮。 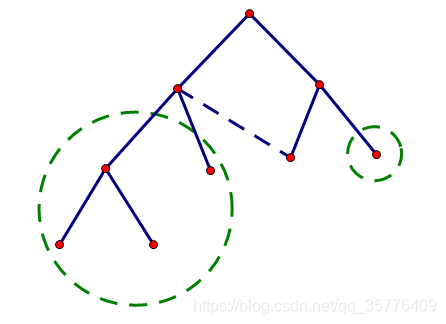 如圖,虛線為新增的邊,綠色圈住的部分都是隻有單個入口的,這些點都必須通過環上的點才能進入,所以這些點可以直接用環上的對應點代替。 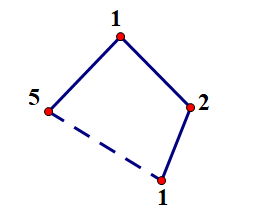 圖中的數字代表這個點代表著多少個點。假設在樹上u,v之間新增邊,那麼可以把u,v到根的路徑以及這條邊看成一個環(也可以是到LCA,不過到根會簡單點),而環上最多有2logn個點,總共在環上的點有2mlogn個,暴力dfs搜尋路徑就可以了。時間複雜度:O((mlogn)22mm)
找了一份程式碼:
// 我是five
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
const int MAXN = 255;
const int Mod = 1e9 + 7;
inline void add_mod(int &x,int y) {
x = (x + y < Mod ? x + y : x + y - Mod);
}
int u[MAXN],v[MAXN];
map<int,int> mp;
inline int get_id(int x) {
if(!mp[x]) mp[x] = (int)mp.size();
return mp[x];
}
vector<int> e[MAXN];
void add_edge(int u,int v) {
e[u].push_back(v);
e[v].push_back(u);
}
inline int cal_size(int u,int n,int d) {
int t = u,c = 0,res;
while(t) c++,t >>= 1;
res = (1 << (d - c + 1))-1,t = c;
while(t < d) t++,u = u << 1 | 1;
return res - max(min(u - n,1 << (d - c)),0);
}
int num[MAXN];
void pre_dp(int u,int f) {
for(auto &v:e[u]) {
if(v == f) continue;
num[u] -= num[v];
pre_dp(v,u);
}
}
int vis[MAXN];
void dfs(int u,int &tot) {
add_mod(tot,num[u]);
vis[u] = 1;
for(auto &v: e[u])
if(!vis[v]) dfs(v,tot);
vis[u] = 0;
}
int main() {
int n,m,d = 0;
scanf("%d%d",&n,&m);
while((1 << d) <= n) d++;
get_id(1);
for(int i=0; i<m; i++) {
scanf("%d%d",&u[i],&v[i]);
int t = u[i];
while(t) get_id(t),t >>= 1;
t = v[i];
while(t) get_id(t),t >>= 1;
}
for(auto &t:mp) {
int u = t.first,id = t.second;
if(u > 1) add_edge(get_id(u),get_id(u >> 1));
num[id] = cal_size(u,n,d);
}
pre_dp(1,0);
for(int i=0; i<m; i++)
add_edge(get_id(u[i]),get_id(v[i]));
int res = 0;
for(int i=1; i<=(int)mp.size(); i++) {
int tot = 0;
dfs(i,tot);
add_mod(res,1LL * tot * num[i] % Mod);
}
printf("%d\n",res);
return 0;
}
