在圖形學中，數學是不可或缺的一部分，所以本書最開始的部分就是數學知識的復習。在圖形學中，最常用的是矢量和矩陣，所以我根據前面三個章節的數學知識，總結一下數學知識。

一、矢量

　 數學中的矢量，擁有方向和長度。其實矢量和點在坐標系中的表示完全一致（笛卡爾坐標系為準），區分矢量和點的關鍵，我覺得就是做平移。點是不能用平移操作來保證一致的，比如點A（1，2，3）經過平移矢量（1，2，3）後就是B（2，4，6），此時就是一個新的點。但是矢量經過相同平移操作後，還是矢量（1，2，3），這是因為矢量表示的是 vector head相對於 vector tail的偏移，平移操作並不會改變這種偏移。

　　在矢量中一個關鍵就是坐標系，數學中的坐標系主要分為左手坐標系和右手坐標系。我時不時會弄混左手和右手坐標系，後來做了一個快捷的記憶：我的頭是y方向，右手伸出來是x方向，那麽如果z方向向前是正方向，那我就處於左手坐標系； 如果我的z方向向後是正方向，那我就處於右手坐標系。所以看起來我的臉決定了我的坐標系：)

矢量的數學操作主要是：加、減、乘三種操作，如果算上求模（求長度），那就是四種操作。A=(x_a,y_a,z_a), B=(x_b,y_b,z_b)

加：A + B = (x_a+x_b, y_a+y_b, z_a+z_b)

　 減：A - B = (x_a-x_b, y_a-y_b, z_a-z_b)

　 乘：A *B = x_ax_b+y_ay_b+z_az_b

模：||A||²= x_a² + y_a2+z_a²

細心的會發現矢量乘的結果變成了一個數，確實，最終的結果就是一個數，其本質就是一種映射或者投影，表示的是A矢量在B矢量方向上的投影長度，矢量的乘可以用公式表示為：

　　A *B = ||A|| *||B|| * sinθ，其中θ為兩個矢量的夾角（由於不熟悉博客的數學公式添加，只有先這寫著了，後面熟練了再修改吧）

矢量中最常見的操作就是歸一化，比如有一個矢量的序列{V₀,v₁,V₂...},如何將這些矢量歸一化為互相垂直的單位矢量？

這兒引入投影的一個表示：proj_n(V)= v . n/||n||， 表示的是v在n的單位矢量上的投影，那麽對於矢量序列，我們可以這樣進行正交歸一化：

1）v₀, v₁,v_2.......

2) w₀ = v₀;

3) w₁ = v₁ - proj_w0(v₁)

4) w₂ = v₂ - proj_w0(v₂) - proj_w1(v₂)

........

根據上面的規律，可以得到正交化的規律：將當前矢量（第一個除外）去除在前面所有矢量上的分量（投影），得到的就是與前面各個適量正交的矢量。

最後我們將正交化的矢量進行歸一化操作，即可得到一組正交歸一化矢量序列。

矢量的最後一個知識點是：矢量的叉積，與矢量點積得到一個投影的結果值不同，矢量的叉積得到的是一個矢量，基本公式為：

AXB = (y_az_b -z_ay_b, z_ax_b - x_az_b, x_ay_b - y_ax_b)，

　 單看公式看不出規律，不過可以這樣理解：xyz, yzx, zxy，分別去掉x, y , z，最後的結果就是三個分量的第一項，然後交換得到三個分量需要減去的第二項

矢量的叉積的實際意義，就是求得一個和A/B兩個矢量都垂直的矢量，這在圖形學中，可以用來求解遊戲對象的一些常用矢量， 比如上(up)/下(down)/左(left)/右(right)/前(forward)/後(back)這些矢量都是互相垂直的，可以利用矢量的叉積得到。註意在笛卡爾坐標系中，矢量的叉積都是左手定律決定方向的，所以AXB和BXA是剛好方向相反的兩個等長矢量。

二、矩陣

　　在圖形學中，我們會繪制各種各樣的遊戲實例，這些實例都是用基本的點（verts）和相關的貼圖（textures）、材質(material)等共同設置渲染狀態的。對於基本的頂點，常常需要做的一個基本操作就是變換：平移、旋轉、縮放等。這些變換操作對應的就是矩陣的變換。

矩陣的定義就不再多說，就是一個nxm的同類元素的集合，通常這個元素就是數字（也可以為其他，這兒不再擴展）。

矩陣最基本的操作可以分為： 矩陣的乘， 矩陣的轉置， 矩陣的行列式， 矩陣的逆

矩陣的乘積： C = AB ≠BA

C矩陣中的每個元素是C_ij是A矩陣的i行和B矩陣j列的對應點積的結果，基於此可以得到A矩陣的列數和B矩陣的行數是相等的（不然怎麽做點積....）

矩陣的轉置A^T，就是將矩陣的行和列對換，說的簡單點就是一列一列的變，新的每列是以前矩陣的每行豎著排列（感覺就是重新排隊）

矩陣的行列式，是一個比較重要的點，Aij作為行列式的代指，就是去除A矩陣的i行和j列後得到的行列式計算結果，整體的公式為：

detA = ∑_j=1ⁿ A_1j(-1)^i+jdetA_1j

可以看出矩陣的行列式計算就是一個遞歸的計算過程，一般在圖形學中的計算不會超過4x4的維度，所以可以用筆算的方式來計算這些矩陣的行列式：）

基於行列式，可以得到一個新的矩陣： 鄰接矩陣A^*，基於基本的矩陣A可以得到一個新的矩陣C_A，其中的元素C_ij = (-1)^i+jdetA_ij，則可以定義鄰接矩陣為：

A^* = C_A^T 基於鄰接矩陣，我們可以得到矩陣A的逆矩陣A^-1 ：A^-1 = A^*/detA

三、變換矩陣

基於矩陣的定義，我們可以將圖形學中的一些常見的變換轉化為對應的變換矩陣，這樣在對點或者矢量進行變換的時候，其對應的數學操作就是一個變換矩陣的操作。基本的變換矩陣可以分為：縮放矩陣， 平移矩陣，旋轉矩陣。

對於變換矩陣對矢量的作用，可以這樣理解：u =(x,y,z) = xi + yj + zk， 那麽一個變換操作可以表示為τ(u) = τ(xi + yj + zk) = xτ(i) + yτ(j) + zτ(k) = [x y z] [τ(i) τ(j) τ(k)]^T = uA

所以說的直白點，就是用矩陣A來表示一種變換操作。那麽具體如何表示呢？可以分拆為基本矩陣，然後進行合並即可。

1、縮放矩陣S

拆開用行向量表示為S(i) = (s_x .1, s_y.0, s_z.0), S(j) = (s_x .0, s_y.1, s_z.0)，S(k) = (s_x .0, s_y.0, s_z.1)

則縮放矩陣可以表示為S = [s_i , s_j, s_k]^T, s_i = (s_x,0,0), s_j = (0,s_y,0), s_k = (0,0,s_z)

2、旋轉矩陣R

其實旋轉矩陣是三個矩陣中相對比較難的矩陣，這兒給出一個旋轉公式：

R_n(V) = proj_n(v) + R_n(V_⊥)

= (n v) n + cosθ V_⊥ + sinθ (n x v)

= cosθ V + (1 - cosθ)(n v)n + sinθ(n x v)

具體的常用的三個旋轉矩陣可以列出來：

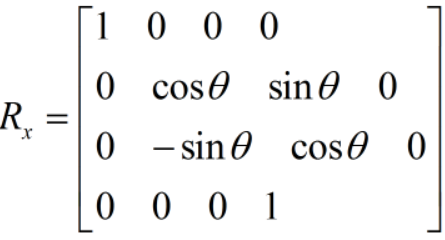
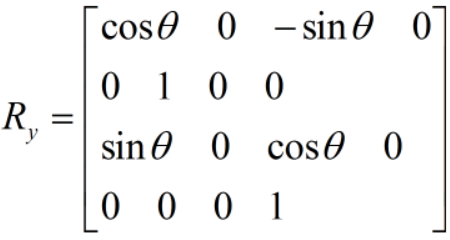
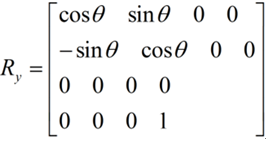
3、平移矩陣T

平移矩陣比較簡單，就不做推算，直接給出結果即可：

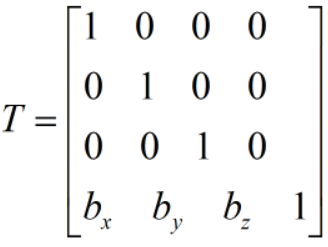
綜合三種基本矩陣，我們可以進行組合得到一個較為復雜的變換矩陣。不過在圖形學的計算中，對於三種矩陣的排序有一定的講究，一般先用縮放矩陣S對當前的變換對象進行縮放，然後用旋轉矩陣R進行旋轉操作，最後用平移矩陣T進行平移操作，所以可以歸並為SRT矩陣。

總結：經過基本的矢量，矩陣和變換的數學知識總結後，接下來就要進入正式的圖形學知識了，我會在後面持續更新~

3D Game Programming withDX11 學習筆記（一） 數學知識總結