基本問題

　　試想我們的美術做了一個3D模型，然後渲染引擎把模型渲染到屏幕上。我們還可以選定不同的視角，模擬不同的光照條件去觀察模型。現在來分析一下這個過程。如果說我們把這個過程看成一個函數，那麽函數的輸出就是屏幕上的圖像。確切地說，是屏幕上的每個像素。這個函數的主要輸入是這個3D模型，我們觀察的視角，光照情況等等因素。渲染過程就是給出這些因素決定每個像素值的過程。

　　首先來看模型。模型通常是由可視化的建模軟件制作，看上去是一個“實體”。然而從計算機的角度來說，模型文件只不過是包含渲染它所需要的數據的文件。真實世界中的物體細節是無法窮盡，極其復雜的。所以我們進行簡化，把物體簡化成多面體，進一步的，簡化成每個面是三角形的多面體。（對於曲面和細節較多的地方，我們可以用更多更小的三角面來擬合）。很顯然，每個頂點的相對位置是重要的。它決定了模型的形狀。由於需要描述位置，自然就有了選擇坐標空間的問題。模型描述自身頂點坐標的空間稱為模型空間。於是我們可以得出模型文件裏一定要包含模型空間下的頂點坐標。

　　通常，在一個渲染的場景中，包含了多個渲染的物體。它們根據不同的位置擺放，當然會構成不同的場景。那麽為了描述場景裏模型之間的相對位置，我們會選擇一個獨立於模型的坐標空間，稱為世界空間。有了世界空間，我們也可以描述觀察者的位置和觀察的角度。這個觀察者，通常我們可以叫它為camera。這樣渲染出來的結果可以視作camera所拍得的圖像。要決定觀察的結果，顯然要知道相機的位置和朝向。另外一點需要指出的是，根據成像投影方式的不同，有正交和透視兩種相機。正交相機裏無法判斷看到的物體離相機的遠近，不存在近大遠小的關系。符合實際人眼觀察結果的是透視相機。物體離相機越遠，所成的像就越小。

　　現在的問題是，給定世界空間中一個點的位置，和相機的位置朝向。我們要確定這個點最後渲染到圖像上哪個位置（它或許是不可見的，這時它也應有一個超出範圍的坐標）由這個問題牽扯到了shader學習中常遇見的坐標變換。首先我們關心的是點相對於相機的位置。所以自然我們可以以相機為準建立一個坐標空間來描述被觀察者的位置。這個空間被稱為view space，觀察空間。按照OPENGL的傳統，我們以相機右方為+x軸，上方為+y軸，觀察方向為-z軸。由此可見觀察空間是一個右手系。在相機觀察的物體中，遠處的物體z值更小。現在問題在於，我們怎樣把world space中的坐標變換到view space中。顯然這是一個仿射變換，由一次線性變換和一次平移構成。3x3的矩陣只能描述線性變換，為統一起見，引入齊次坐標。將線性變換的矩陣擴充為4x4的矩陣，添加一列（或者一行，取決於使用行向量還是列向量）用於刻畫平移。現在任意兩個三維坐標空間的仿射變換都可以用一個4x4的矩陣來描述。

　　得到了頂點在相機空間的坐標，現在需要決定這個點投影在屏幕上的坐標。首先我們先將這個坐標歸一化變換到一個左手系的剪裁空間中，使得點的坐標只有三維，並且任何一個分量超出-1到1範圍的點都不在可視範圍內。(openGL傳統，directx則是0到1)

　　正交相機的可視範圍是坐標滿足約束

　　-Far <= z <= -Near,

　　-Size <= y <= Size,

　　-Size*Aspect <= x <= Size*Aspect

　　的點。這裏Size和Aspect決定了相機所看到的矩形範圍，Far和Near決定了深度範圍。現在我們需要通過一個變換，把三個分量的邊界映射到-1和1上。由於要改變手性，我們讓-Far映射到1，-Near映射到-1.

　　解方程組

　　-k * Far + b = 1,

　　-k * Near + b = -1.

　　得出系數為 k= -2 / (Far - Near), b = (Near + Far) / (Near - Far)

　　於是得出變換矩陣

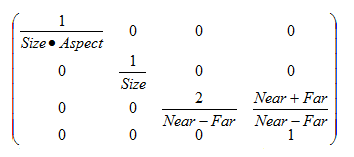
　　對於透視相機，它的可視範圍是一個四棱臺，或者說視錐體。定義相機豎直方向的張角為FOV，水平和豎直方向可視距離之比為Aspect。它的可視約束為（註意z為負數）

　　tan(FOV/2)*z*Aspect <= x <= -tan(FOV/2)*z*Aspect

　　tan(FOV/2)*z <= y <= -tan(FOV/2)*z

　　-Far<= z <= -Near

　　這裏由於x，y同時還受到z的約束，因此我們需要利用w分量做齊次化，矩陣最後一行的第三個元素應為-1.使得最後的結果中w分量和變換前的z分量互為相反數。

　　和上面類似，-Far映射到Far，-Near映射到-Near.

　　解方程組

　　k*(-Far) + b = Far

　　k*(-Near) + b = -Near 得出 k = (Far + Near) / (Near - Far) b = 2Far*Near / (Near - Far)

　　從而得出透視相機的變換矩陣

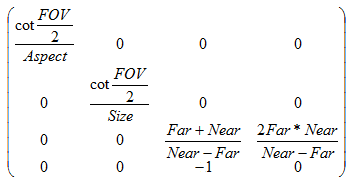
　　利用變換矩陣左乘坐標的列向量，然後利用w分量做齊次除法即可得到歸一化以後的坐標（x，y，z）對於可見的點，它每一個分量都在-1到1的範圍內。對x，y將其加1除以2再分別乘以屏幕的像素寬高即可得到最終渲染的像素坐標。（opengl的屏幕坐標原點在左下角）z值則是這一點的深度值。

　　現在我們來總結一下完成這一系列變換所需要知道的量。

　　模型空間下的頂點坐標----->>觀察空間下的頂點坐標 這一步需要知道觀察者和被觀察者的相對位置關系，才能給出模型空間到觀察空間的變換矩陣。顯然，模型和相機在場景中擺好以後，這個矩陣自然也就知道了。

　　觀察空間的頂點坐標 ------->>剪裁空間 這一步只需要知道相機相關的參數。深度範圍Far-Near，正交相機的size，透視相機的FOV，觀察的寬高比Aspect。

　　剪裁空間----->> 屏幕像素坐標 只需要指定好像素寬高即可。

Unity Shader學習筆記（一）坐標變換