C語言實現粒子群算法(PSO)二
上一回說了基本粒子群算法的實現,並且給出了C語言代碼。這一篇主要講解影響粒子群算法的一個重要參數---w。我們已經說過粒子群算法的核心的兩個公式為:
Vid(k+1)=w*Vid(k)+c1*r1*(Pid(k)-Xid(k))+c2*r2*(Pgd(k)-Xid(k))
Xid(k+1) = Xid(k) + Vid(k+1)
標紅的w即是本次我們要討論的參數。之前w是不變的(默認取1),而現在w是變化的,w稱之為慣性權重,體現的是粒子繼承先前速度的能力。 經驗表明:一個較大的慣性權重有利於全局搜索,而一個較小的慣性權重則更有利於局部搜索。為了更好地平衡算法的全局搜索能力與局部搜索能力,Shi.Y提出了線性遞減慣性權重(LDIW)
即:w(k) = w_end + (w_start- w_end)*(Tmax-k)/Tmax。其中w_start 為初始慣性權重,w_end 為叠代至最大次數時的慣性權重;k為當前叠代次數, Tmax為最大叠代次數。一般來說,w_start=0.9,w_end=0.4時,算法的性能最好。這樣隨著叠代的進行,慣性權重從0.9遞減到0.4,叠代初期較大的慣性權重使算法保持了較強的全局搜索能力。而叠代後期較小的慣性權重有利於算法進行更精確的局部搜索。線性慣性權重,只是一種經驗做法,常用的慣性權重還包括 以下幾種。
(3) w(k) = w_start - (w_start-w_end)*(k/Tmax)^2
(4) w(k) = w_start + (w_start-w_end)*(2*k/Tmax - (k/Tmax)^2)
(5) w(k) = w_end*(w_start/w_end)^(1/(1+c*k/Tmax)) ,c為常數,比如取10等。
本例的目的就是比較這5種不同的w取值,對於PSO尋優的影響。比較的方法為每種w取值,重復實驗若幹次(比如100次),比較平均最優解的大小,陷入次優解的次數,以及接近最優解的次數。 這樣對於5種方法的優劣可以有一個直觀的比較。
代碼如下:

/*
* 使用C語言實現粒子群算法(PSO) 改進版本
* 參考自《MATLAB智能算法30個案例分析》
* update: 16/12/3
* 主要改進的方面體現在w的選擇上面
* 本例的尋優非線性函數為
* f(x,y) = sin(sqrt(x^2+y^2))/(sqrt(x^2+y^2)) + exp((cos(2*PI*x)+cos(2*PI*y))/2) - 2.71289
* 該函數有很多局部極大值點,而極限位置為(0,0),在(0,0)附近取得極大值
*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define c1 1.49445 //加速度因子一般是根據大量實驗所得
#define c2 1.49445
#define maxgen 300 // 叠代次數
#define repeat 100 // 重復實驗次數
#define sizepop 20 // 種群規模
#define popmax 2 // 個體最大取值
#define popmin -2 // 個體最小取值
#define Vmax 0.5 // 速度最大值
#define Vmin -0.5 //速度最小值
#define dim 2 // 粒子的維數
#define w_start 0.9
#define w_end 0.4
#define PI 3.1415926 //圓周率
double pop[sizepop][dim]; // 定義種群數組
double V[sizepop][dim]; // 定義種群速度數組
double fitness[sizepop]; // 定義種群的適應度數組
double result[maxgen]; //定義存放每次叠代種群最優值的數組
double pbest[sizepop][dim]; // 個體極值的位置
double gbest[dim]; //群體極值的位置
double fitnesspbest[sizepop]; //個體極值適應度的值
double fitnessgbest; // 群體極值適應度值
double genbest[maxgen][dim]; //每一代最優值取值粒子
//適應度函數
double func(double * arr)
{
double x = *arr; //x 的值
double y = *(arr+1); //y的值
double fitness = sin(sqrt(x*x+y*y))/(sqrt(x*x+y*y)) + exp((cos(2*PI*x)+cos(2*PI*y))/2) - 2.71289;
return fitness;
}
// 種群初始化
void pop_init(void)
{
for(int i=0;i<sizepop;i++)
{
for(int j=0;j<dim;j++)
{
pop[i][j] = (((double)rand())/RAND_MAX-0.5)*4; //-2到2之間的隨機數
V[i][j] = ((double)rand())/RAND_MAX-0.5; //-0.5到0.5之間
}
fitness[i] = func(pop[i]); //計算適應度函數值
}
}
// max()函數定義
double * max(double * fit,int size)
{
int index = 0; // 初始化序號
double max = *fit; // 初始化最大值為數組第一個元素
static double best_fit_index[2];
for(int i=1;i<size;i++)
{
if(*(fit+i) > max)
max = *(fit+i);
index = i;
}
best_fit_index[0] = index;
best_fit_index[1] = max;
return best_fit_index;
}
// 叠代尋優,傳入的參數為一個整數,取值為1到5,分別代表5種不同的計算w的方法
void PSO_func(int n)
{
pop_init();
double * best_fit_index; // 用於存放群體極值和其位置(序號)
best_fit_index = max(fitness,sizepop); //求群體極值
int index = (int)(*best_fit_index);
// 群體極值位置
for(int i=0;i<dim;i++)
{
gbest[i] = pop[index][i];
}
// 個體極值位置
for(int i=0;i<sizepop;i++)
{
for(int j=0;j<dim;j++)
{
pbest[i][j] = pop[i][j];
}
}
// 個體極值適應度值
for(int i=0;i<sizepop;i++)
{
fitnesspbest[i] = fitness[i];
}
//群體極值適應度值
double bestfitness = *(best_fit_index+1);
fitnessgbest = bestfitness;
//叠代尋優
for(int i=0;i<maxgen;i++)
{
for(int j=0;j<sizepop;j++)
{
//速度更新及粒子更新
for(int k=0;k<dim;k++)
{
// 速度更新
double rand1 = (double)rand()/RAND_MAX; //0到1之間的隨機數
double rand2 = (double)rand()/RAND_MAX;
double w;
double Tmax = (double)maxgen;
switch(n)
{
case 1:
w = 1;
case 2:
w = w_end + (w_start - w_end)*(Tmax-i)/Tmax;
case 3:
w = w_start -(w_start-w_end)*(i/Tmax)*(i/Tmax);
case 4:
w = w_start + (w_start-w_end)*(2*i/Tmax-(i/Tmax)*(i/Tmax));
case 5:
w = w_end*(pow((w_start/w_end),(1/(1+10*i/Tmax))));
default:
w = 1;
}
V[j][k] = w*V[j][k] + c1*rand1*(pbest[j][k]-pop[j][k]) + c2*rand2*(gbest[k]-pop[j][k]);
if(V[j][k] > Vmax)
V[j][k] = Vmax;
if(V[j][k] < Vmin)
V[j][k] = Vmin;
// 粒子更新
pop[j][k] = pop[j][k] + V[j][k];
if(pop[j][k] > popmax)
pop[j][k] = popmax;
if(pop[j][k] < popmin)
pop[j][k] = popmin;
}
fitness[j] = func(pop[j]); //新粒子的適應度值
}
for(int j=0;j<sizepop;j++)
{
// 個體極值更新
if(fitness[j] > fitnesspbest[j])
{
for(int k=0;k<dim;k++)
{
pbest[j][k] = pop[j][k];
}
fitnesspbest[j] = fitness[j];
}
// 群體極值更新
if(fitness[j] > fitnessgbest)
{
for(int k=0;k<dim;k++)
gbest[k] = pop[j][k];
fitnessgbest = fitness[j];
}
}
for(int k=0;k<dim;k++)
{
genbest[i][k] = gbest[k]; // 每一代最優值取值粒子位置記錄
}
result[i] = fitnessgbest; // 每代的最優值記錄到數組
}
}
// 主函數
int main(void)
{
clock_t start,finish; //程序開始和結束時間
start = clock(); //開始計時
srand((unsigned)time(NULL)); // 初始化隨機數種子
for(int i=1;i<=5;i++)
{
int near_best = 0; // 接近最優解的次數
double best_sum = 0; // 重復最優值求和
double best = 0; // 重復實驗得到的最優解
for(int j=0;j<repeat;j++)
{
PSO_func(i); // 第i種w參數取值
double * best_fit_index = max(result,maxgen);
double best_result = *(best_fit_index+1); //最優解
if(best_result > 0.95)
near_best++;
if(best_result>best)
best = best_result;
best_sum += best_result;
}
double average_best = best_sum/repeat; //重復實驗平均最優值
printf("w參數的第%d種方法:\n",i);
printf("重復實驗%d次,每次實驗叠代%d次,接近最優解的實驗次數為%d次,求得最優值為:%lf,平均最優值為:%lf\n",repeat,maxgen,near_best,best,average_best);
}
finish = clock(); //結束時間
double duration = (double)(finish - start)/CLOCKS_PER_SEC; // 程序運行時間
printf("程序運行耗時:%lf\n",duration);
return 0;
}
程序運行結果如下:
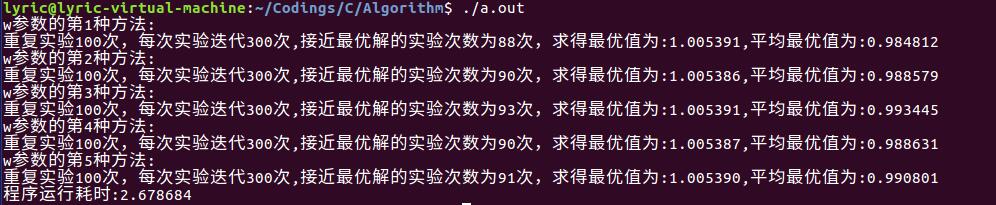
從實驗的結果來看,第3種w的取法,無論是接近最優解的的次數,最優值大小,還是平均最優值,都是5種裏面最好的。其原因解釋如下:通過w的表達式可以看出,前期w變化較慢,取值較大,維持了算法的全局搜索能力;後期w變化變化較快,極大地提高了算法的局部搜索能力尋優能力,從而取得了很好的求解效果。
從總體上來看,在大部分的情況下,無論w是5種裏面哪種取法,得到的結果都很好地接近實際的最優解,這說明了粒子群算法的搜索尋優能力還是很強的。
C語言實現粒子群算法(PSO)二
