【算法設計與分析基礎】11、廣度優先遍歷
阿新 • • 發佈:2017-05-21
append path str src http adt ise uil tor
package cn.xf.algorithm.ch03;
import java.util.ArrayDeque;
import java.util.Iterator;
import java.util.Queue;
import org.junit.Test;
/**
*
* 功能:廣度優先遍歷
* @author xiaofeng
* @date 2017年5月21日
* @fileName BFS.java
*
*/
public class BFS {
public void breadthFirstSearch(int graph[][], char points[], int marks[]) {
//初始化所有標記
for(int i = 0; i < marks.length; ++i) {
marks[i] = 0;
}
//遍歷所有節點
for(int i = 0; i < points.length; ++i) {
//判斷是否已經遍歷被標記,如果沒有,就作為一個新的樹的起始節點
if(marks[i] == 0) {
//沒有被標記
StringBuilder paths = new StringBuilder(points[i] + "");
//開始廣度遍歷
marks[i] = 1;
bfsc(graph, points, marks, i, paths);
System.out.println(paths.toString());
}
}
}
/**
* 廣度優先遍歷一顆樹
* @param graph
* @param points
* @param marks
* @param firstIndex
* @param paths
*/
public void bfsc(int graph[][], char points[], int marks[], int firstIndex, StringBuilder paths) {
//創建隊列,存放當前節點的所有子女節點,索引
Queue queue = new ArrayDeque<Integer>();
queue.add(firstIndex);
//下層的子女節點的所有集合
//遍歷隊列,並且把下級子節點添加到新隊列中,等待下次遍歷
//只要隊列不為空,就不點遍歷,到葉子節點
while(!queue.isEmpty()) {
//取出當前的前向節點,遍歷其下所有子女節點,隊列中有數據
//獲取並移除此雙端隊列所表示的隊列的頭
int temp = (Integer) queue.poll(); //獲取隊列頭
//獲取其後面的可達節點
for(int i = 0; i < points.length; ++i) {
int arrayNum = graph[temp][i]; //是否可達,並且還要判斷是否已經被標記
if(marks[i] == 0 && arrayNum != 0) {
//如果這個節點可達並且沒有被標記,就把這個節點添加到隊列中
paths.append(" => " + points[i]);
marks[i] = 1; //從新標記節點
queue.add(i);
}
}
}
}
@Test
public void test1() {
BFS bfs = new BFS();
//a,b,c,d,e,f,g,h,i,j一共10個節點,兩顆樹
//以下是矩陣圖,0表示不相連,1表示相連,節點本身自己到自己為0
int graph[][] = {
// a,b,c,d,e,f,g,h,i,j
{0,0,1,1,1,0,0,0,0,0}, //a 到其他節點
{0,0,0,0,1,1,0,0,0,0}, //b 到其他節點
{1,0,0,1,0,1,0,0,0,0}, //c 到其他節點
{1,0,1,0,0,0,0,0,0,0}, //d 到其他節點
{1,1,0,0,0,1,0,0,0,0}, //e 到其他節點
{0,1,1,0,1,0,0,0,0,0}, //f 到其他節點
{0,0,0,0,0,0,0,1,0,1}, //g 到其他節點
{0,0,0,0,0,0,1,0,1,0}, //h 到其他節點
{0,0,0,0,0,0,0,1,0,1}, //i 到其他節點
{0,0,0,0,0,0,1,0,1,0} //j 到其他節點
};
char points[] = {‘A‘, ‘B‘, ‘C‘, ‘D‘, ‘E‘, ‘F‘, ‘G‘, ‘H‘, ‘I‘, ‘J‘};
int marks[] = {0,0,0,0,0,0,0,0,0,0};
bfs.breadthFirstSearch(graph, points, marks);
}
}
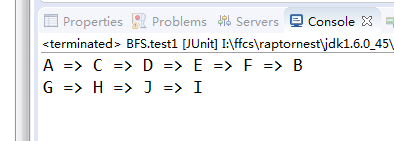
結果:
【算法設計與分析基礎】11、廣度優先遍歷
