【強連通分量縮點】【拓撲排序】【dp預處理】CDOJ1640 花自飄零水自流,一種相思,兩處閑愁。
阿新 • • 發佈:2017-05-26
如果 vector brush algo blog pri cmp 處理 ret
題意: 在n個點m條邊的有向圖上,從1出發的回路最多經過多少個不同的點 可以在一條邊上逆行一次
題解: 在同一個強連通分量中,顯然可以經過當中的每一個點 因此先將強連通分量縮點,點權為強連通分量的點數
如果不逆行,那麽答案就是1所在的強連通分量的點數 如果逆行了,那麽逆行的邊必然在縮點後的拓撲圖上
假設逆行的邊為u->v,那麽該回路可分為1到v和u到1兩部分 經過的最多點數即1到v與u到1路徑上的最大點權和減去1的點權 (這裏的點指的都是縮點後的點)
例子中在邊4->3上逆行就能從1出發經過所有點回到1
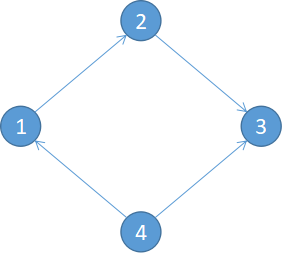
那麽預處理拓撲圖上1到每個點的最大點權和及每個點到1的最大點權和(將邊倒過來搞一次就行) 枚舉逆行的邊即可得到答案。
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
vector<int>G[100010],rG[100010],vs;
bool used[100010];
int cmp[100010],x[100010],y[100010],a[100010],f[100010],g[100010],ru[100010],ru2[100010];
int n,m,K;
void dfs(int U){
used[U]=1;
for(int i=0;i<G[U].size();++i){
if(!used[G[U][i]]){
dfs(G[U][i]);
}
}
vs.push_back(U);
}
void rdfs(int U){
used[U]=1;
cmp[U]=K;
for(int i=0;i<rG[U].size();++i){
if(!used[rG[U][i]]){
rdfs(rG[U][i]);
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d%d",&x[i],&y[i]);
G[x[i]].push_back(y[i]);
rG[y[i]].push_back(x[i]);
}
for(int i=1;i<=n;++i){
if(!used[i]){
dfs(i);
}
}
memset(used,0,sizeof(used));
for(int i=vs.size()-1;i>=0;--i){
if(!used[vs[i]]){
++K;
rdfs(vs[i]);
}
}
for(int i=1;i<=n;++i){
G[i].clear();
rG[i].clear();
}
for(int i=1;i<=m;++i){
if(cmp[x[i]]!=cmp[y[i]]){
G[cmp[x[i]]].push_back(cmp[y[i]]);
++ru[cmp[y[i]]];
rG[cmp[y[i]]].push_back(cmp[x[i]]);
++ru2[cmp[x[i]]];
}
}
for(int i=1;i<=n;++i){
++a[cmp[i]];
}
queue<int>q;
for(int i=1;i<=K;++i){
if(!ru[i]){
q.push(i);
}
}
memset(f,0xaf,sizeof(f));
f[cmp[1]]=a[cmp[1]];
while(!q.empty()){
int U=q.front(); q.pop();
for(int i=0;i<G[U].size();++i){
f[G[U][i]]=max(f[G[U][i]],f[U]+a[G[U][i]]);
--ru[G[U][i]];
if(!ru[G[U][i]]){
q.push(G[U][i]);
}
}
}
for(int i=1;i<=K;++i){
if(!ru2[i]){
q.push(i);
}
}
memset(g,0xaf,sizeof(g));
g[cmp[1]]=a[cmp[1]];
while(!q.empty()){
int U=q.front(); q.pop();
for(int i=0;i<rG[U].size();++i){
g[rG[U][i]]=max(g[rG[U][i]],g[U]+a[rG[U][i]]);
--ru2[rG[U][i]];
if(!ru2[rG[U][i]]){
q.push(rG[U][i]);
}
}
}
int ans=a[cmp[1]];
for(int i=1;i<=m;++i){
if(cmp[x[i]]!=cmp[y[i]]){
ans=(int)max((ll)ans,(ll)f[cmp[y[i]]]+(ll)g[cmp[x[i]]]-(ll)a[cmp[1]]);
}
}
printf("%d\n",ans);
return 0;
}【強連通分量縮點】【拓撲排序】【dp預處理】CDOJ1640 花自飄零水自流,一種相思,兩處閑愁。
