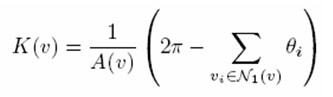好久沒有寫代碼了，最近拿計算三角網格表面的高斯曲率練了練手，並實現了高斯曲率的可視化，復習了一點微分幾何的知識。感覺有時候還是要自己把代碼寫出來，調試運行，結合試驗結果，才能對相應的知識有更深的了解。

所謂曲面上某點的高斯曲率，即該點兩個主曲率的乘積。把曲面上的頂點映射到單位球的球心,把法線的端點映射到球面上，即將曲面上的點與球面上的點建立了一種對應，叫做曲面的球面表示，也叫高斯映射。高斯曲率的幾何意義，即球面上的面積/曲面局部面積的極限，可以看出，高斯曲率確實反映了曲面局部的彎曲程度。

利用高斯曲率的正負性，可以很方便地研究曲面在一點鄰近的結構，高斯曲率K>0為橢圓點，K<0為雙曲點，K=0為平面或拋物點。並且高斯曲率是曲面的內蘊量，只與曲面的第一基本型相關，與坐標軸的選取和參數化表示無關。

言歸正傳，求解三角網格表面的高斯曲率，就需要利用離散微分幾何，我采用的公式為：

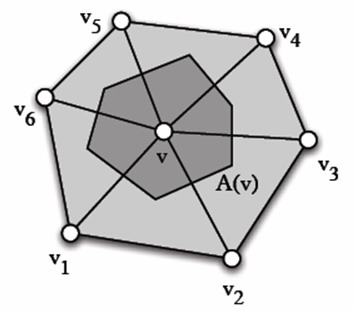
這個公式的幾何意義是比較直觀的，2*Pi-該點鄰域三角形對應的角度和，再除以相應區域的面積，就刻劃了該點曲面的彎曲程度。

其實推導出上述公式的方法是非常巧妙的,仔細研究一下,它利用了在高斯映射的幾何意義下,離散高斯曲率對局部曲面的積分
考慮p點鄰域法線映射到單位球上的面積,即近似為 2*Pi-該點鄰域三角形對應的角度和
不仔細寫了,大家看看下面這張圖,感受一下這個公式的美妙:

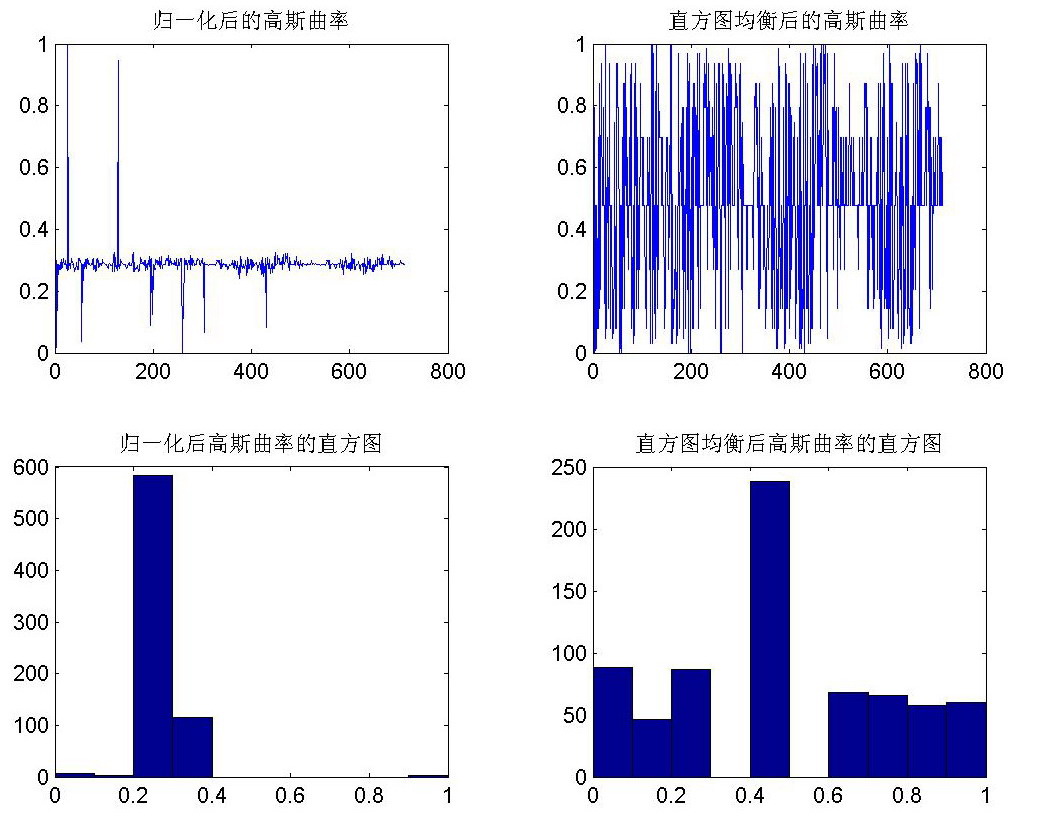
具體的編碼比較簡單，求出GaussCurvature數組後，歸一化到[0,1]，設定三種顏色c1灰黃，c2綠，c3紅，線性加權偽彩顯示。K>0顯示為綠色，K<0顯示為紅色，K=0顯示為灰黃色，顏色越鮮艷，高斯曲率的絕對值越大。實現效果如下圖

顯示效果不好，搞過圖像處理的人就知道了，需要做一個直方圖均衡

直方圖均衡後的顯示效果為：

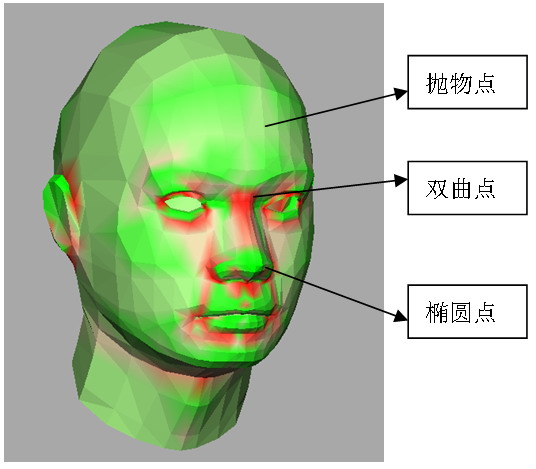
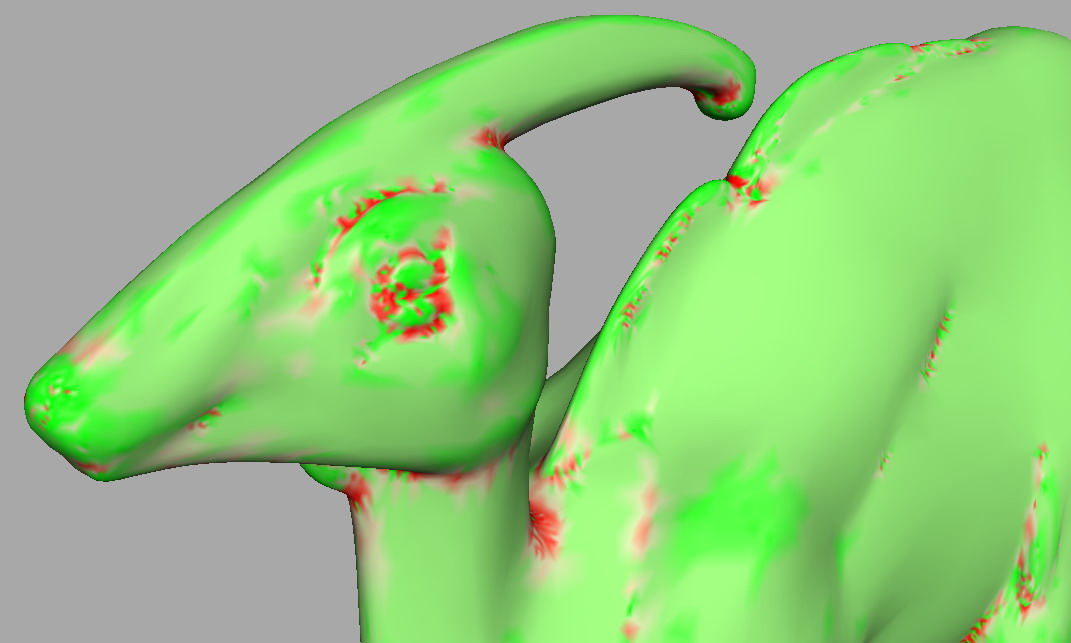
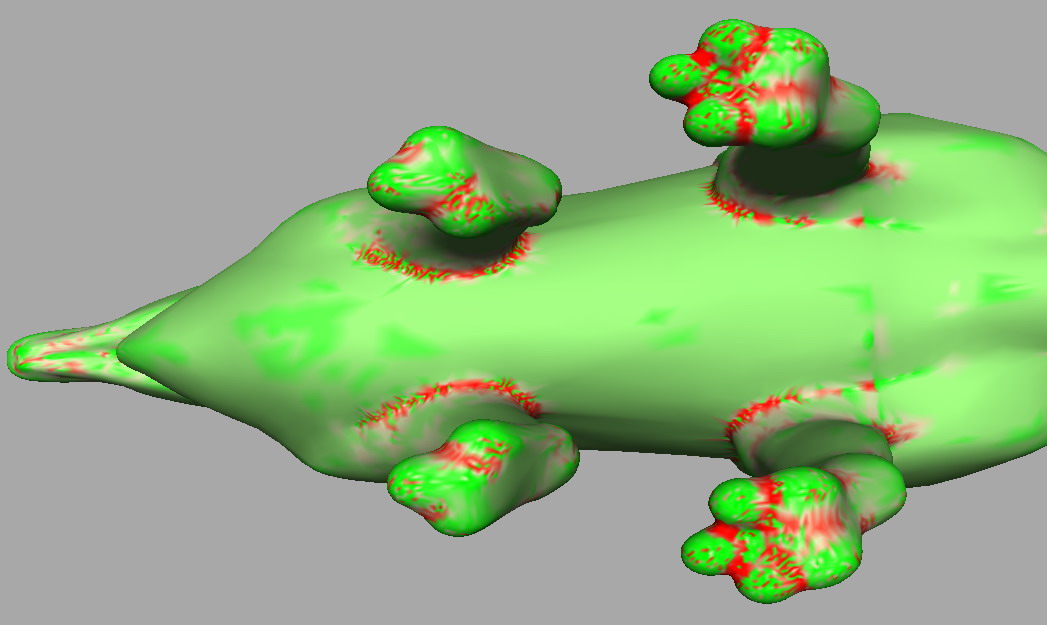
這樣的效果就好多了，鼻梁處紅色的為典型的雙曲點（兩個主曲率異號,主方向的兩條法截線,一條向法線的正向彎曲,一條向法線的反向彎曲,形成馬鞍面），鼻尖處綠色的為典型的拋物點（兩個主曲率同號,曲面沿所有方向都朝向同一側彎曲），腦門處較平坦的區域（有一個主曲率接近0）高斯曲率的絕對值較小，顏色也比較淡。

貼出更多的試驗圖片，計算高斯曲率並偽彩顯示，確實可以直觀地看出曲面的一些屬性，應該可以指導網格去噪、平滑、簡化、分割等後繼的研究

三角網格上離散高斯曲率的計算公式比較簡單，做了這個簡單的練習，把網格表面頂點屬性可視化的程序框架搭建好了。以後有機會也可以實現一下平均曲率，主曲率，主方向的計算。

三角網格表面高斯曲率的計算與可視化