1 堆棧

1.1 堆棧的概念

　　表達式求值問題

　　　　表達式 = 運算數 + 運算符號

　　　　不同的運算符號優先級不一樣

　　一般地, 運算是見到運算符號進行運算, 但是在一般的表達式中, 運算符號前面的值我們能夠知道, 但是後面的值不一定是當前運算符運算的值, 因此這個運算增加了很大的困難

　　中綴表達式: 運算符位於兩個運算數之間

　　後綴表達式: 運算符位於兩個運算數之後

前綴表達式, 前中後綴表達式的轉換

　　後綴表達式的求值順序:

　　　　從左往右依次掃描, 遇到運算符就運算, 運算的運算數是就近就近就近的兩個運算數

62/3-42*+ = ?
62
 
/ -> 3
33- -> 0
042* -> 08
08+ -> 8

　　完成這種後入先出的效果的就是堆棧(Stack)

　　　　堆棧只在一端(棧頂TOP)做插入和刪除

　　　　棧頂TOP: 堆棧中離出口最近的那一個元素的位置

　　　　插入數據: 入棧(Push)

　　　　刪除數據: 出棧(Pop)

　　　　後進先出: LIFO

　　堆棧元素出現的順序的可能性

　　有ABC三個順序輸入, 輸出的結果不可能是CAB

1.2 堆棧的順序存儲

　　棧的順序存儲結構通常由一個一維數組和一個記錄棧頂元素位置的變量組成

　　其中Top不是一個指針, 而是一個整數, 默認的時候為-1, 當進入一個元素之後加1

　　當Top=-1時表示棧為空

　　1) 入棧

　　2) 出棧

　　關於使用一個數組實現兩個堆棧的問題

　　如果將數組對半分, 自己存自己的, 這樣有可能存在空間浪費, 為了避免空間浪費

　　應該設計兩個堆棧都是從數組的兩端向裏存儲

　　當兩個堆棧的Top指針相遇(也就是相鄰了, 值相差1了)時, 堆棧就滿了

　　出入棧

1.3 堆棧的鏈式存儲

　　棧的鏈式存儲結構實際上就是一個單鏈表, 叫做鏈棧

　　插入和刪除只能在鏈棧的棧頂進行

　　由於單鏈表在鏈尾無法找到前一個元素, 因此用單鏈表存儲堆棧的時候, 選擇鏈頭作為棧頂

　　初始化和判空

　　出棧入棧操作

1.4 堆棧的應用

　　將中綴表達式轉化為後綴表達式

　　特點: 運算數的相對順序是不變的, 只是運算符號順序發生改變

　　處理辦法:

　　　　從左往右讀, 遇到運算數就輸出

　　　　遇到運算符的時候, 判斷運算符與堆棧中運算符的優先級, 如果堆棧的優先級高, 就彈出, 再比較堆棧的符號與當前的符號直到小於當前的運算符為止; 如果堆棧的運算符優先級低就把當前的運算符壓如堆棧中

　　　　註意, 在堆棧中的括號優先級是最低的, 當遇到右括號的時候就可以彈出內容了, 直到遇到左括號結束

　　堆棧的其他應用諸如:

　　　　函數調用以及遞歸的實現

　　　　深度優先搜索

　　　　回溯算法

　　　　...

2 隊列

　　隊列具有一定操作約束的線性表

　　　　插入和刪除: 只能在一端插入, 在另一端刪除

　　　　特點: 先進先出FIFO

2.1 隊列的順序存儲的實現

　　隊列的順序存儲結構通常是由一個一維數組和記錄隊列列頭和列尾元素的兩個變量組成, 記錄列頭元素位置的變量是front, 記錄隊尾元素位置的變量是rear

　　front和rear是整形數據, 記錄的是數組的下標

　　一般的一維數組表示的隊列, front和rear都是-1, 當新增數據時, rear加1, 當輸出數據的時候, front加1

　　　　rear是最後一個元素的下標

　　　　front是第一個元素前一個位置的下標

　　由於這樣會造成資源浪費, 因此產生了循環隊列

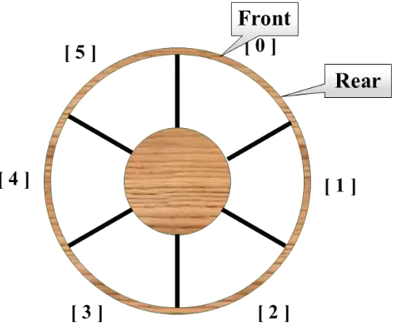
　　當front=rear的時候, 表示隊列為空

　　但是如果這麽設定的話, 一直存存滿的時候, front和rear又相等了, 這樣就無法判斷是空還是滿了

　　解決方案:

　　　　1) 使用額外的標記, size或者tag(判斷最後一次操作是添加還是刪除)

　　　　2) 僅僅使用n-1個數組空間(一般采用這樣的方式)

Mooc數據結構-02堆棧和隊列