本講內容

1. Newton‘s method（牛頓法）

2. Exponential Family（指數簇）

3. Generalized Linear Models(GLMs)（廣義線性模型）

1.牛頓法

假如有函數, 尋找使得

牛頓法的步驟如下：

(1) initialize as some value. 上圖中用 初始化 的值

(2) 在這一點上對f求值得到，之後計算這一點的導數值

(3) 作該點的切線，得到與橫軸的交點的值，此為牛頓法的一次叠代。

更新公式為

我們可以使用牛頓法取代梯度上升法作極大似然估計

對對數似然函數， want s.t.

對於一次叠代，

通常來說，牛頓法對函數f有一定的要求（具體沒說），牛頓法對logistic函數效果很好。

的初始值並不會對牛頓法收斂的結果產生影響。

牛頓法的收斂屬於二次收斂（每一次叠代都會使誤差的數量級乘方），正常情況下速度會比二次收斂慢，但是依然比梯度下降法快。

牛頓法的一般化：

H is the Hessian matrix（黑塞矩陣）

牛頓法的缺點是，當特征數量過大的時候，求黑塞矩陣的逆會耗費相當長的時間。

2.指數簇

指數簇的一般形式

-自然參數(natural parameter)

- 充分統計量(sufficient statistic) 通常情況下（伯努利分布或者高斯分布）: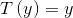

固定a,b,T， 改變的值， 會得到一組不同的概率分布。

伯努利分布和高斯分布都是指數分布簇的特例

對於伯努利分布

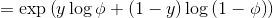
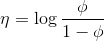
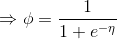
對於高斯分布

考慮到方差對最終結果沒有影響， 在這裏設置

指數分布族還包括很多其他的分布：
多項式分布（multinomial）
泊松分布（poisson）：用於計數的建模
伽馬分布（gamma），指數分布（exponential）:用於對連續非負的隨機變量進行建模
β分布，Dirichlet分布：對小數建模

3.廣義線性模型(GLMS)

為了導出廣義線性模型，首先制定三個假設：

(1)

(2) Given , goal is to output

　 want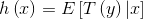

(3) 即自然參數與特征向量之間是線性相關的

對於伯努利分布

在上節的指數簇中推導出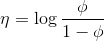

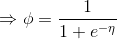
而根據假設(3)

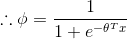
我們的目標是輸出

由上節知

而

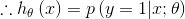
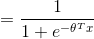
該函數即為logistic 函數

對於高斯分布

在最小二乘估計中，我們假設響應變量是連續的，且服從高斯分布

我們的目標是輸出

由上節知

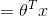
順帶一提

正則響應函數（canonical response function）：
正則鏈接函數（canonical link function）:

4.Softmax回歸（多類分類問題）

多項式分布

這k個參數是冗余的，所以 我們定義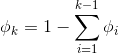

在後面的過程中，我們將不使用 這個參數

多項式分布屬於指數分布簇，但是

在這裏按照如下定義

...

都是k-1維的向量

引入指示函數,

用 表示向量 的第個元素，則

where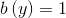

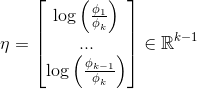
反過來，

為了減少參數冗余，定義

由GLMS的假設3:

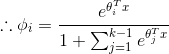
所以我們可以得到需要的假設

這種方法是logistic回歸的推廣，應用於多分類問題。

優化目標依然是極大似然估計

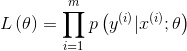
其中

使用梯度上升法或者牛頓法解得最優參數

第四講完。

（筆記）斯坦福機器學習第四講--牛頓法