大小 限制 總結 情況 pca 空間 會有 ges nal

1. 問題

真實的訓練數據總是存在各種各樣的問題：
　　1、 比如拿到一個汽車的樣本，裏面既有以“千米/每小時”度量的最大速度特征，也有“英裏/小時”的最大速度特征，顯然這兩個特征有一個多余。
　　2、 拿到一個數學系的本科生期末考試成績單，裏面有三列，一列是對數學的興趣程度，一列是復習時間，還有一列是考試成績。我們知道要學好數學，需要有濃厚的興趣，所以第二項與第一項強相關，第三項和第二項也是強相關。那是不是可以合並第一項和第二項呢？
　　3、 拿到一個樣本，特征非常多，而樣例特別少，這樣用回歸去直接擬合非常困難，容易過度擬合。比如北京的房價：假設房子的特征是（大小、位置、朝向、是否學區房、建造

年代、是否二手、層數、所在層數），搞了這麽多特征，結果只有不到十個房子的樣例。要擬合房子特征‐>房價的這麽多特征，就會造成過度擬合。
　　4、 這個與第二個有點類似，假設在 IR 中我們建立的文檔‐詞項矩陣中，有兩個詞項為“learn”和“study”，在傳統的向量空間模型中，認為兩者獨立。然而從語義的角度來講，兩者是相似的，而且兩者出現頻率也類似，是不是可以合成為一個特征呢？
　　5、 在信號傳輸過程中，由於信道不是理想的，信道另一端收到的信號會有噪音擾動，那麽怎麽濾去這些噪音呢？
　　回顧我們之前介紹的《模型選擇和規則化》，裏面談到的特征選擇的問題。但在那篇中要剔除的特征主要是和類標簽無關的特征。比如“學生的名字”就和他的“成績”無關，使用的是互信息的方法。
　　而這裏的特征很多是和類標簽有關的，但裏面存在噪聲或者冗余。在這種情況下，需要一種特征降維的方法來減少特征數，減少噪音和冗余，減少過度擬合的可能性。
下面探討一種稱作主成分分析（PCA）的方法來解決部分上述問題。 PCA 的思想是將 n維特征映射到 k 維上（k<n），這 k 維是全新的正交特征。這 k 維特征稱為主元，是重新構造出來的 k 維特征，而不是簡單地從 n 維特征中去除其余 n‐k 維特征。

2. PCA 計算過程

　　整個 PCA 過程貌似及其簡單，就是求協方差的特征值和特征向量，然後做數據轉換。

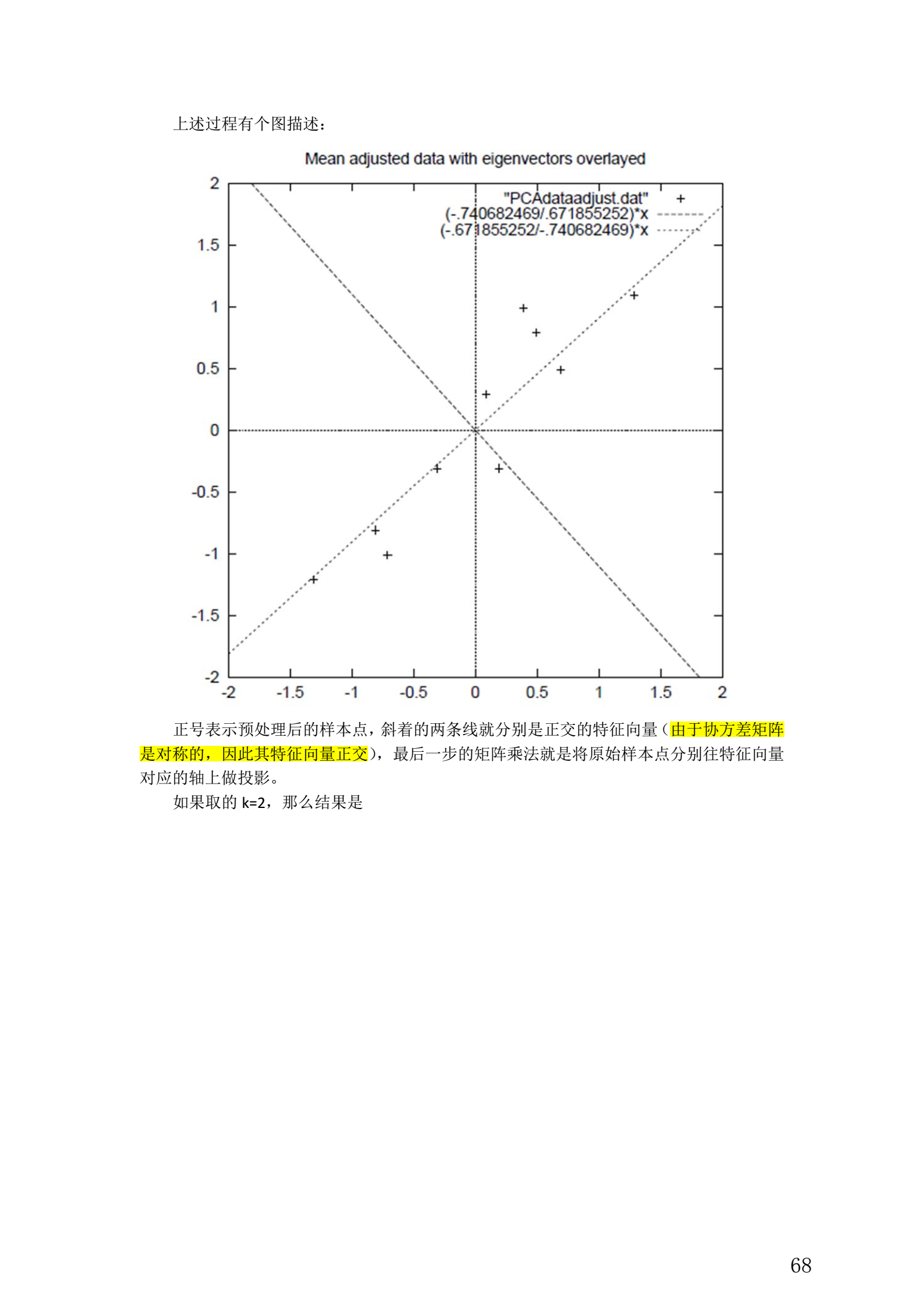
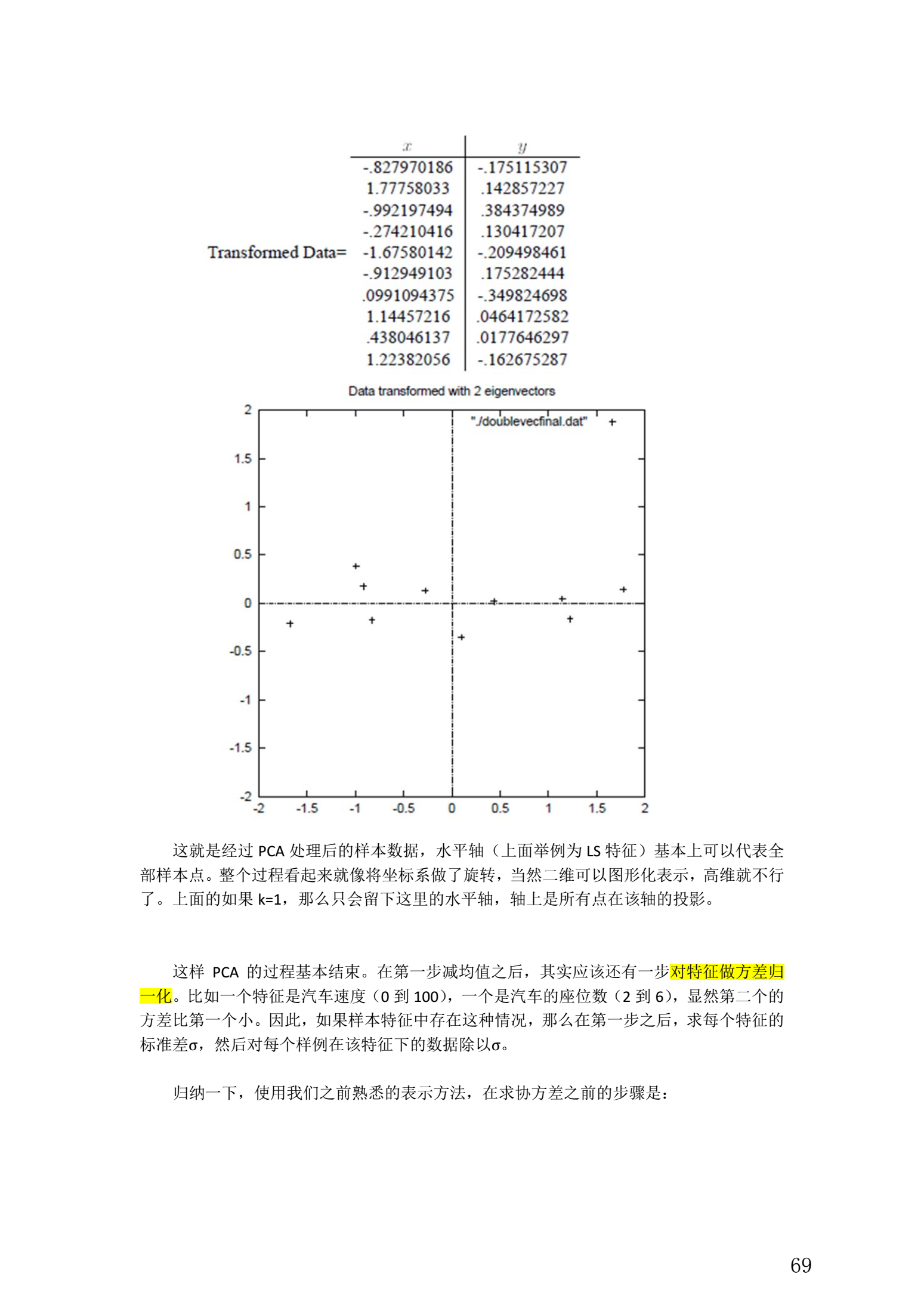
5. 總結與討論

• PCA 技術的一大好處是對數據進行降維的處理。我們可以對新求出的“主元”向量的重要性進行排序，根據需要取前面最重要的部分，將後面的維數省去，可以達到降維從而簡化模型或是對數據進行壓縮的效果。同時最大程度的保持了原有數據的信息。

• PCA 技術的一個很大的優點是，它是完全無參數限制的。在 PCA 的計算過程中完全不需要人為的設定參數或是根據任何經驗模型對計算進行幹預，最後的結果只與數據相關，與用戶是獨立的。　
• 但是，這一點同時也可以看作是缺點。如果用戶對觀測對象有一定的先驗知識，掌握了數據的一些特征，卻無法通過參數化等方法對處理過程進行幹預，可能會得不到預期的效果，效率也不高。
• 在非高斯分布的情況下， PCA方法得出的主元可能並不是最優的

• 另外 PCA 還可以用於預測矩陣中缺失的元素
  
  

【機器學習】主成分分析PCA（Principal components analysis）