Convolution Network及其變種(反卷積、擴展卷積、因果卷積、圖卷積)
今天,主要和大家分享一下最近研究的卷積網絡和它的一些變種。

首先,介紹一下基礎的卷積網絡。

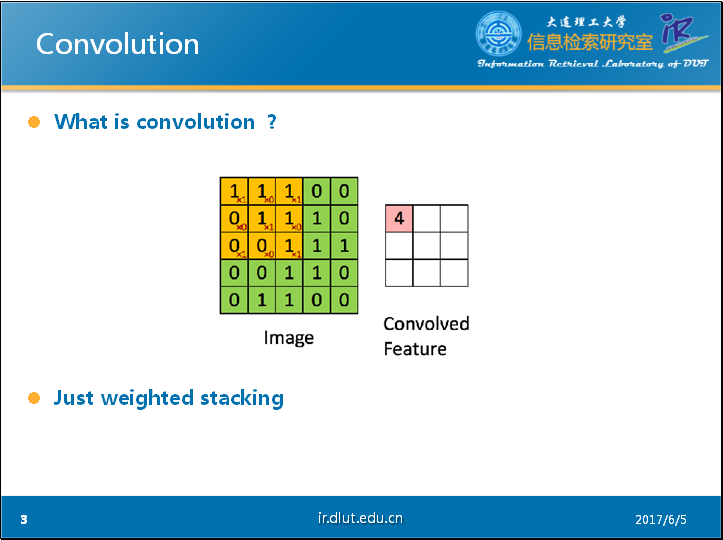
通過PPT上的這個經典的動態圖片可以很好的理解卷積的過程。圖中藍色的大矩陣是我們的輸入,黃色的小矩陣是卷積核(kernel,filter),旁邊的小矩陣是卷積後的輸入,通常稱為feature map。
從動態圖中,我們可以很明白的看出卷積實際上就是加權疊加。
同時,從這個動態圖可以很明顯的看出,輸出的維度小於輸入的維度。如果我們需要輸出的維度和輸入的維度相等,這就需要填充(padding)。
現在我們來看看由padding帶來的不同的Conv NN。

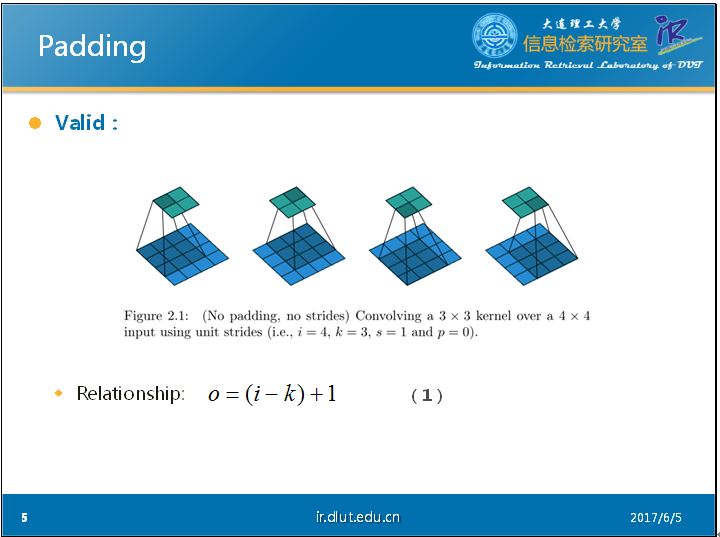
首先,我們來看一下不填充(valid)的Conv NN。
我們可以從PPT中的這個靜態的圖片看出:輸出維度O、卷積核的維度K和輸入維度I存在如下關系(公式-1)。其中,我們假定input和kernel都是正方形的,因此,我們可以用4表示4*4的input,3表示3*3的kernel。
當input的維度和output的維度相同時,這種padding叫做same padding。同時也叫做half padding。同樣,我們可以根據PPT中的圖片看出在包含padding的conv時,輸出維度和輸入維度對應的關系(公式-2)。其中,p表示padding的維度,在此處,我們同樣假定會在長和寬這兩個維度進行相同數目的padding。
當我們進行k/2的padding時,我們運用剛才的公式(公式-2)可以得到如下結果。同時如果k是奇數(2n+1),則通過推導可知剛好output維度 = input 維度。

當我們對輸入數據的順序很註重的時候,因果卷積(causal conv)便可以發揮作用。
Causal最初跟隨WaveNets一起提出。WaveNets是一個生成模型,主要用來生成音樂。WaveNets是利用卷積來學習t時刻之前的輸入數據(音頻),來預測t+1時刻的輸出。也就是說,該模型輸出的最後的X的概率會是如公式-3 所示。在公式-3 和PPT中的動態圖片中,我們可以看出,t時刻的輸出僅僅依賴於1,2,…,t-1時刻的輸入,不會依賴於t+1時刻以及之後時刻的輸入。這與BiLSTM的思想截然不同。
當你的模型有這種特殊要求時,便可以采用casual。
在實現上,1D的casual 主要是通過padding來實現的。在2D的casual 主要是通過mask filter map來實現的。

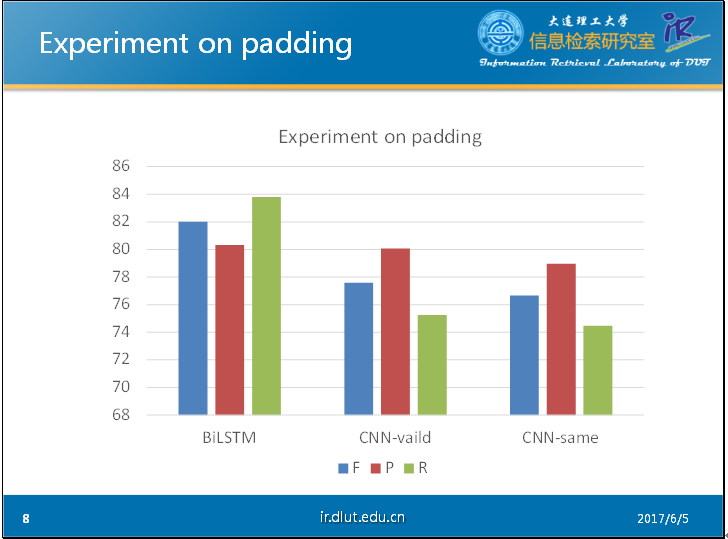
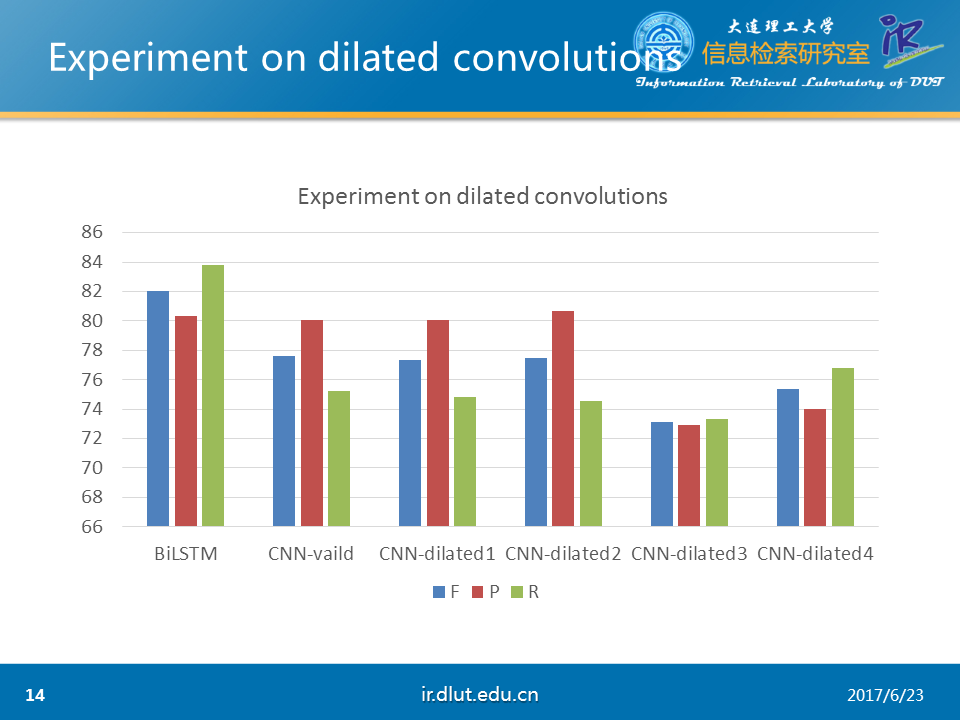
以下是我在CHEMDNER數據集下做的簡單的實驗。其中輸入采用的窗口大小為11. 從圖中可以明顯看出,沒有經過仔細調參的CNN明顯弱於BiLSTM,而valid形式的CNN要好於經過padding的CNN。這可能是由於padding會帶來噪音,幹擾模型。
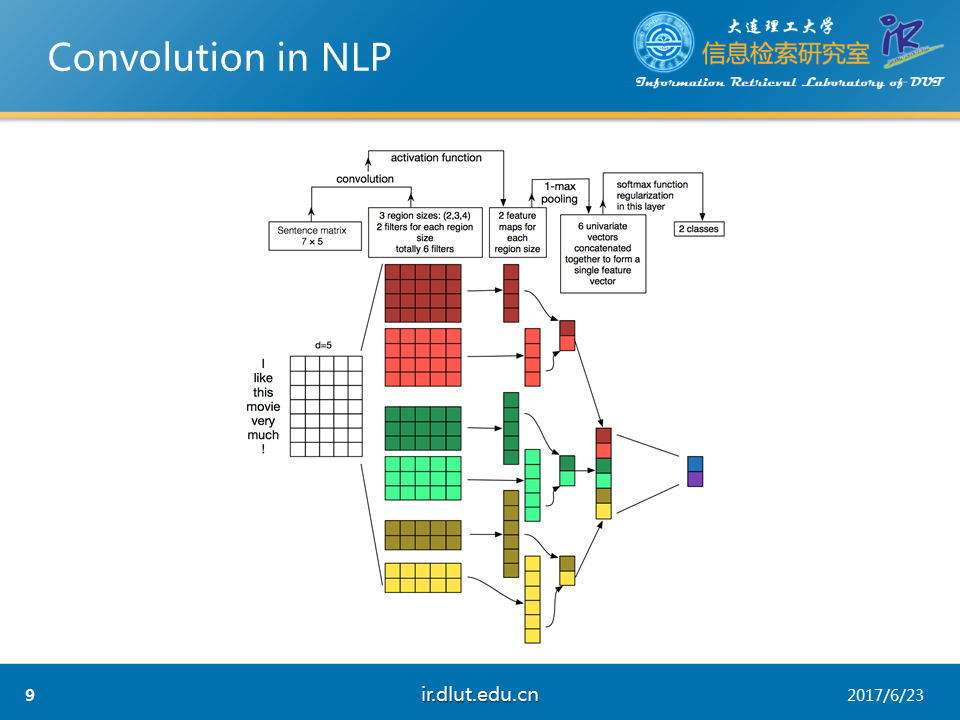
下圖,展示了利用CNN來進行NLP任務的流程。可以發現一般會使用多通道的CNN來學習輸入的特征,並采用不同的kernel以及pooling。
下面,我們來看一下另一種卷積,擴展卷積(dilated)。擴展卷積目前在NLP上沒有應用。主要是用於圖像。

Dilated conv在ICLR 2016上提出。其主要作用是在不增加參數和模型復雜度的條件下,可以指數倍的擴大視覺野(每一個輸出是由視覺野大小的輸入所決定的)的大小。從下圖中可以看出這一效果。藍色的矩形表示視覺野。紅色的小點表示kernel。在圖a中,kernel是3*3,視覺野是3*3,dilated=1;在圖b中,kernel是3*3,但是視覺野是7*7,dilated=2;在圖c中,kernel是3*3,但是視覺野是15*15,dilated=4. 可以看出在dilated(擴展系數)擴大時,視覺野同樣擴大。
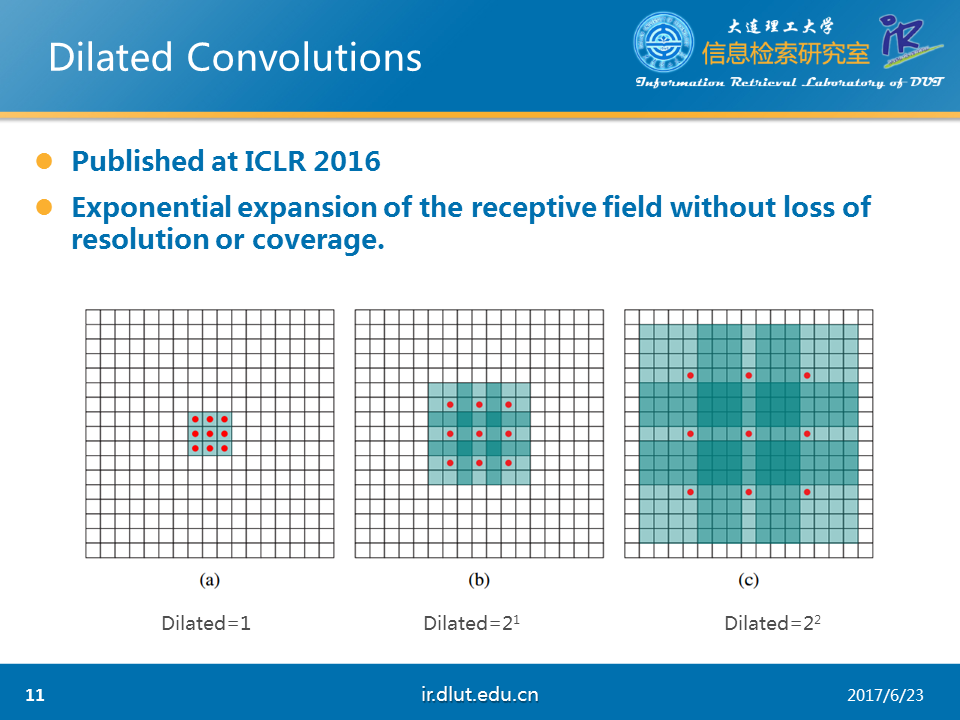
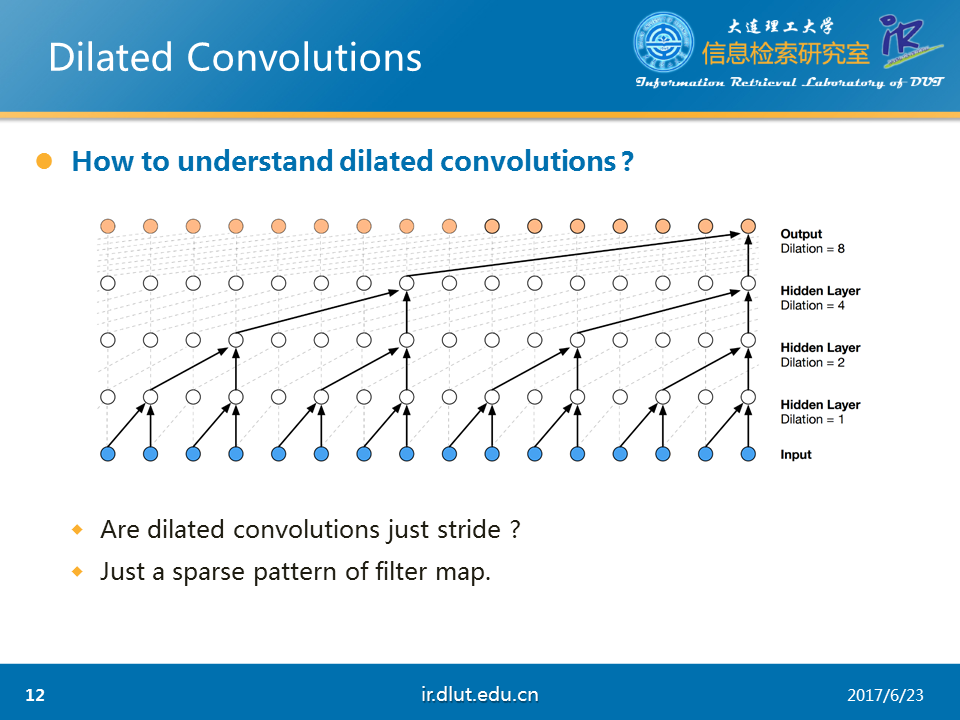
下面,我們使用1D的數據來詳細看一下dilated。從下圖可以看出,當dilated=2時,每一個輸出,“看到了”3個輸入(雖然其中2-1=1被忽略了)。當dilated=4時,“看到了”5個輸入(4-1=3個被忽略了)
從上面的分析可以看出,dilated與stride非常相似。但dilated與stride可以等同嗎?
答案是否定的。我們可以將dilated看成是kernel稀疏化的一種模式。而stride只是dilated的一種特例。根據不同任務,我們可以設計不同的稀疏模式。並不一定要求在寬上的稀疏個數定於長上的稀疏個數。
下圖是,論文中給出的效果。該任務是場景分割。Dilated是第4列,標準答案是第5列。可以看出dilated的結果好於其他模型。

下圖同樣是在CHEMDNER數據集下做的實驗。可以看出dilated較小時與普通CNN性能相同。但較大時性能降低。
由於dilated會稀疏化kernel,所以可能對於NER任務不太適合。但是對於文檔分類、關系抽取可能效果會好一些。
下面,我們來看一下反卷積(deconvolution)

我要講的這篇論文是在CVPR 2010上發表。
Deconv在數學上,是反轉卷積的效果。在deconv時,我們僅僅知道h,需要求f和g。然而,在conv時,我們知道g,通過正向傳播和方向傳播來修改f來得到最好的h。
目前,deconv在實際生活中已經用於信號處理、圖像處理等方面。
在deep learning上,主要用於以下三個方面。
l unsupervised learning: 重構圖像
l CNN可視化:將conv中得到的feature map還原到像素空間,來觀察特定的feature map對哪些pattern的圖片敏感
l Upsampling:上采樣。

Deconv又被稱為轉置的卷積(transposed conv)。
我們可以將圖中conv的過程用矩陣相乘的形式寫出來。其中C表示圖中的第一個矩陣。X表示第二個矩陣。Y表示第三個矩陣。在公式的兩邊,同時乘C的轉置便可得到反卷積。
由此可知,在前向傳播是使用C,後向傳播時使用CT便是普通的conv。反之,則是deconv。

下面,介紹一下deconv在圖像重構上的應用。該任務主要是抽取圖像的特征。下圖是論文提供的結果。可以看出效果不錯。

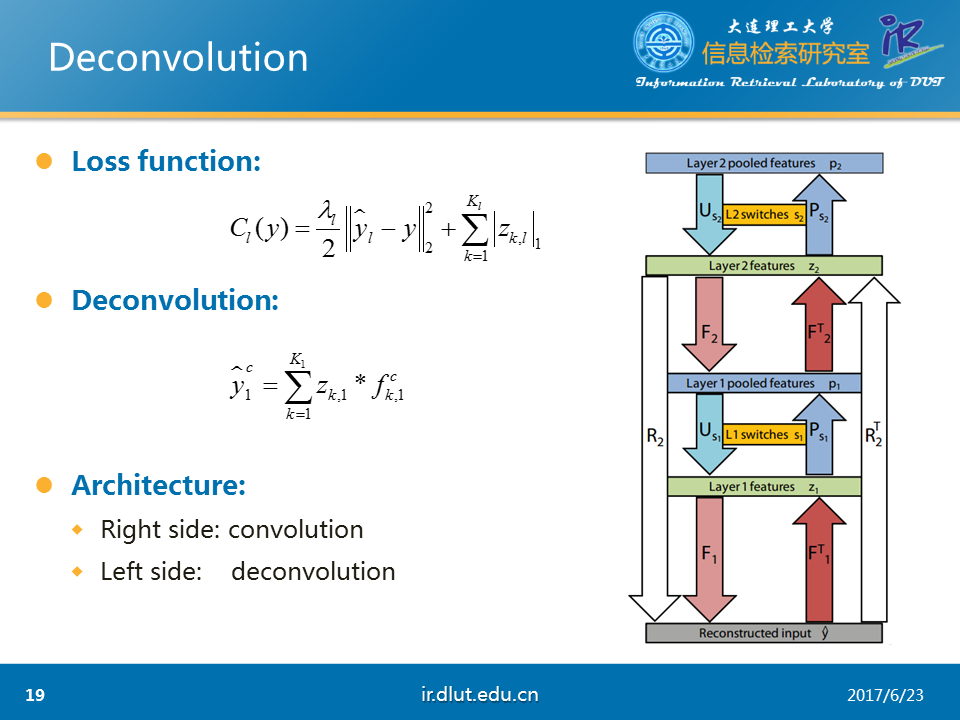
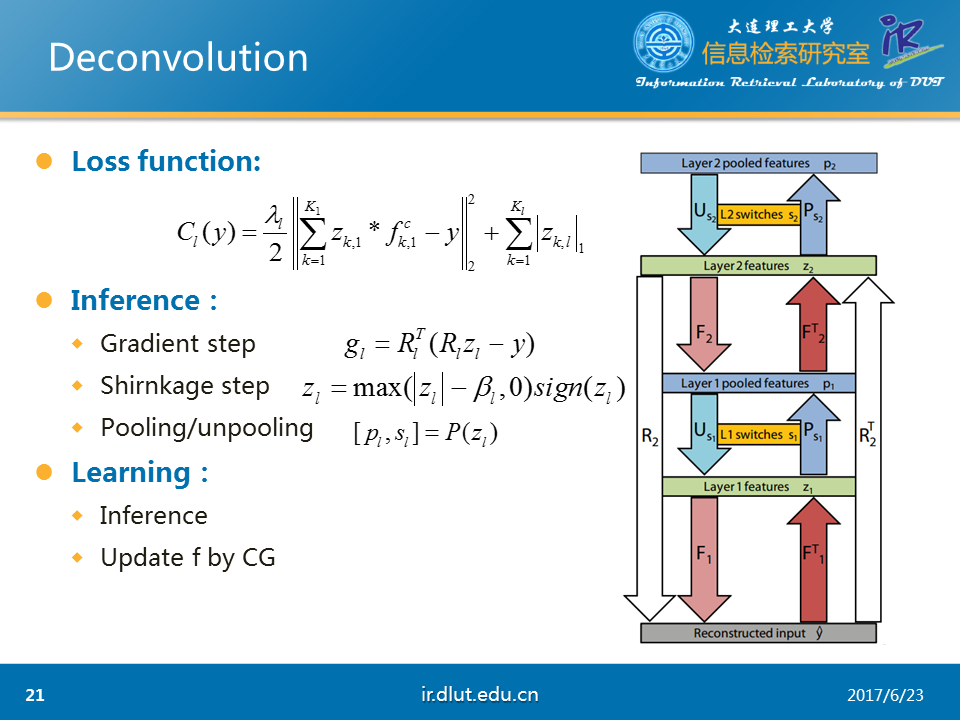
該任務采用的loss如圖所示,是典型的重構誤差+L1正則。
采用的deconv公式如下。表示重構的輸入,z表示conv下的feature map,也就是我們任務的結果,f表示kernel。
旁邊的圖是系統的大概流程。圖中F表示deconv,FT表示conv,P表示pool,U表示unpool。R表示F,U,F操作的聯合。RT同理。
在一般的流程中(例如利用CNN來做圖像分類時),我們首先將圖像的像素點經過FT操作輸入到z1層,然後通過P操作,然後得到第一層的輸出。隨後經過第二層的FT、P操作後,同樣可以得到第二層的輸出。隨後,我們便可以用這個第二層的輸出來做相關的任務。比如做圖像分類。
但是在deconv中,我們需要反向這一個過程。在開始,假設我們的模型已經訓練好了。我的任務是那手上的第二層的輸出(同樣假設我們已經得到),經過U操作、F操作,可以得到第一層的輸出。隨後再次經過相同的操作後,可以得到重構的輸入。由於我們假設模型已經訓練好了,故重構的輸入與原始的輸入相差會非常小。
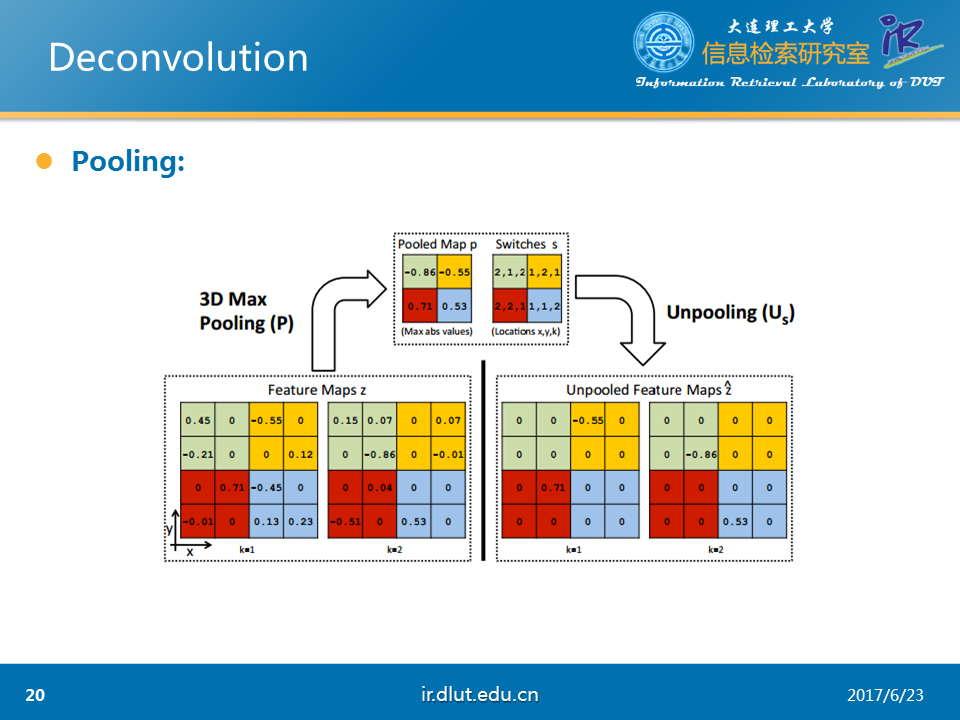
下圖是論文中所采用的3D pooling。與我們熟悉的2D的pooling的不同是3D pooling首先經過2D pooling後,然後在不同的feature map之間再pool一次。所以是3D的。
而unpooling便是3D pooling 的反向過程。
經過3D pooling 和Unpooling後,可以看出結果稀疏了很多。這也是任務的需求。
介紹完大概流程,下面我們來了解一下模型如何訓練。由於在deconv中f和g都不知道,所以需要固定f來最優化g和固定g來最優化f。具體來說,在本任務中,deconv中的filter,圖片的feature map(z)未知,我們僅僅只知道原始的y,我們需要得到圖片的z,也就是在前幾頁PPT中展示的圖片的輪廓圖。
為了便於理解,我們將使用訓練好的模型稱為inference,訓練模型稱為learning。Inference對應於固定f,最優化z。learning首先會進行inference操作後,然後再固定z,最優化f。
在inference過程中,分為三個步驟,首先在gradient step時,利用反向傳播,可以得到loss對於z的梯度。用該梯度更新z。隨後,在shirnkage step上,利用圖示的函數來稀疏化z,其中,beta是超參。最後,在Pooling step上,經過P操作,便可以得到最後的第二層的輸出。總的來說,在inference過程中,我們會重復執行這3步,直到發現最後的loss足夠小。
在learning過程中,我們先經過inference後,然後再利用CG算法在固定z下,最優化f。重復經過這兩步後,直到發現最後的loss足夠下,則該模型已經訓練好。
局部連接層(Locally-connected layers)是conv的一個擴展。在conv中,所有的W都是共享的。但是在locally中,所有的參數並不是共享的。也就是說,在計算上,locally同樣會利用W進行conv(加權疊加),但是這個W每個輸入都會不一樣。
Locally與conv相比,由於W不共享,因而模型能學習到更復雜的特征。同時也越容易過擬合。

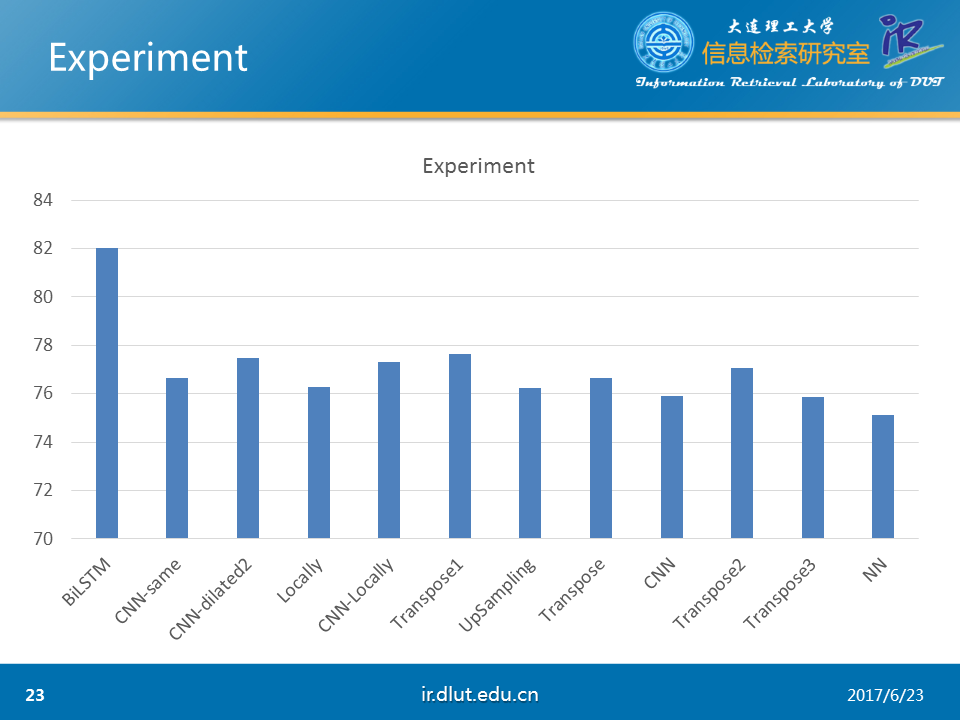
下圖同樣是在CHEMDNER下做的實驗。可以看出反卷積(transpose)微好於CNN-same。
下面介紹一下,圖卷積(graph convolution)。

我們首先不介紹graph conv的理論。我們首先介紹如何使用graph conv。
首先,我們知道圖 G =(V,E),其中X表示頂點集V的特征,A表示圖的結構信息,通常使用鄰接矩陣。在一層的graph conv中,使用上層的輸出Hl,A和本層的W作為輸入,經過某種函數映射f後,便可以得到本層的輸出。
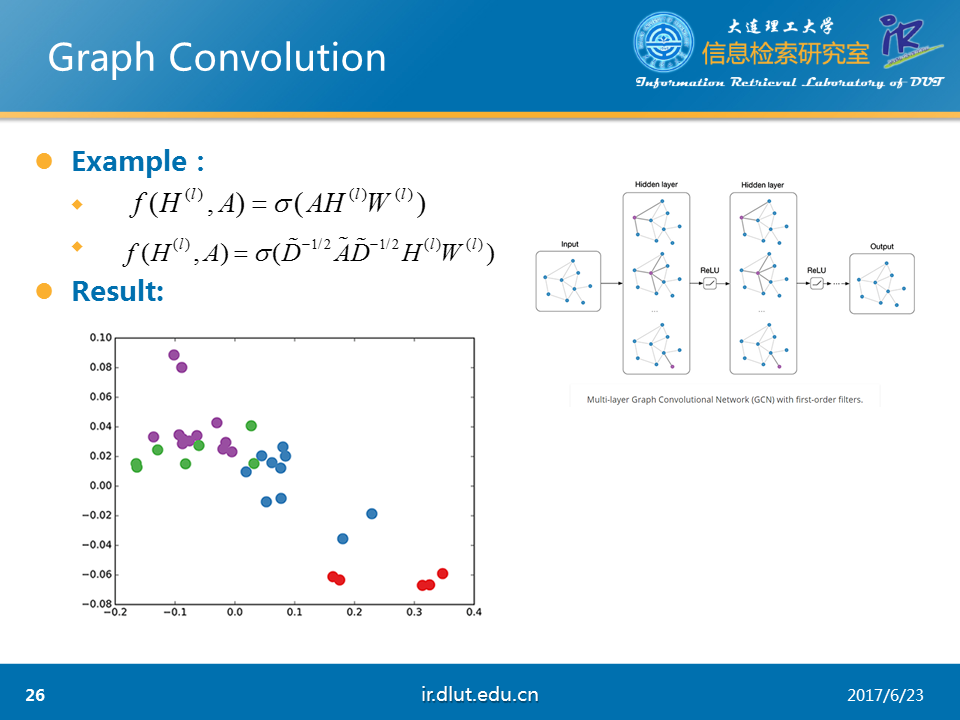
下面,我們假設使用如圖所示的函數σ。由於A是圖的鄰接矩陣,所以只有在當前點與其他點有連接的時候才會有值。這樣AHW就會表示當前節點的所有鄰居在上一層的輸出乘以W。這樣,我們通過函數σ就僅僅看到了當前點的局部連接。這與conv的局部連接非常相似。因此,我們可以從這一點來理解graph conv。同時,當我們使用多層的graph conv時,H2會利用H1的值,H1利用的是當前節點的1介鄰居的信息,而H2便是利用當前節點1介和2介鄰居的信息。

我們利用剛才函數的復雜版,在karate-club數據集上,隨機初始化W,使用3層的graph conv,將最後的H3輸出來,便可以得到如圖的結果。可以看到在未訓練時,節點之間的向量距離還不錯(相同顏色的點距離較近)。
圖中Ahat=A+I,Dhat表示Ahat節點度的對角矩陣。
在理論上,我們可以通過兩種途徑來解釋graph conv。
l 在頻譜圖理論中,卷積可以表示為矩陣的乘積。將該公式-4運用chebyshev多項式和其他的近似,我們可以得到公式-5.而公式-5 與我們剛才使用的函數σ是基本相同的。
l W-L算法告訴我們,我們可以使用當前節點的鄰居表示它。

下面來做一下總結。

總結如下圖所示。其中dilated可能在文本分類、關系抽取上會取得較好效果。


Convolution Network及其變種(反卷積、擴展卷積、因果卷積、圖卷積)
