對深度可分離卷積、分組卷積、擴張卷積、轉置卷積(反捲積)的理解
轉自:https://blog.csdn.net/chaolei3/article/details/79374563
參考:
https://zhuanlan.zhihu.com/p/28749411
https://zhuanlan.zhihu.com/p/28186857
https://blog.yani.io/filter-group-tutorial/
https://www.zhihu.com/question/54149221
http://blog.csdn.net/guvcolie/article/details/77884530?locationNum=10&fps=1
http://blog.csdn.net/zizi7/article/details/77369945
https://github.com/vdumoulin/conv_arithmetic
https://www.zhihu.com/question/43609045/answer/130868981
1. 深度可分離卷積(depthwise separable convolution)
在可分離卷積(separable convolution)中,通常將卷積操作拆分成多個步驟。而在神經網路中通常使用的就是深度可分離卷積(depthwise separable convolution)。
舉個例子,假設有一個3×3大小的卷積層,其輸入通道為16、輸出通道為32。
那麼一般的操作就是用32個3×3的卷積核來分別同輸入資料卷積,這樣每個卷積核需要3×3×16個引數,得到的輸出是隻有一個通道的資料。之所以會得到一通道的資料,是因為剛開始3×3×16的卷積核的每個通道會在輸入資料的每個對應通道上做卷積,然後疊加每一個通道對應位置的值,使之變成了單通道,那麼32個卷積核一共需要(3×3×16)×32 =4068個引數。
1.1 標準卷積與深度可分離卷積的不同
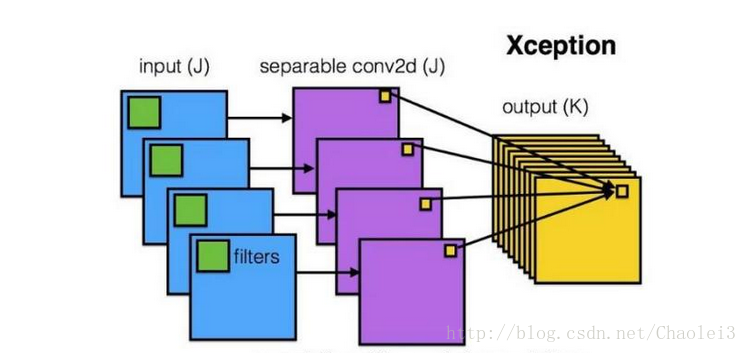
用一張來解釋深度可分離卷積,如下:
可以看到每一個通道用一個filter卷積之後得到對應一個通道的輸出,然後再進行資訊的融合。而以往標準的卷積過程可以用下面的圖來表示:
1.2 深度可分離卷積的過程
而應用深度可分離卷積的過程是①用16個3×3大小的卷積核(1通道)分別與輸入的16通道的資料做卷積(這裡使用了16個1通道的卷積核,輸入資料的每個通道用1個3×3的卷積核卷積),得到了16個通道的特徵圖,我們說該步操作是depthwise(逐層)的,在疊加16個特徵圖之前,②接著用32個1×1大小的卷積核(16通道)在這16個特徵圖進行卷積運算,將16個通道的資訊進行融合(用1×1的卷積進行不同通道間的資訊融合),我們說該步操作是pointwise(逐畫素)的。這樣我們可以算出整個過程使用了3×3×16+(1×1×16)×32 =656個引數。
1.3 深度可分離卷積的優點
可以看出運用深度可分離卷積比普通卷積減少了所需要的引數。重要的是深度可分離卷積將以往普通卷積操作同時考慮通道和區域改變成,卷積先只考慮區域,然後再考慮通道。實現了通道和區域的分離。
2 分組卷積(Group convolution)
Group convolution 分組卷積,最早在AlexNet中出現,由於當時的硬體資源有限,訓練AlexNet時卷積操作不能全部放在同一個GPU處理,因此作者把feature maps分給多個GPU分別進行處理,最後把多個GPU的結果進行融合。
2.1 什麼是分組卷積
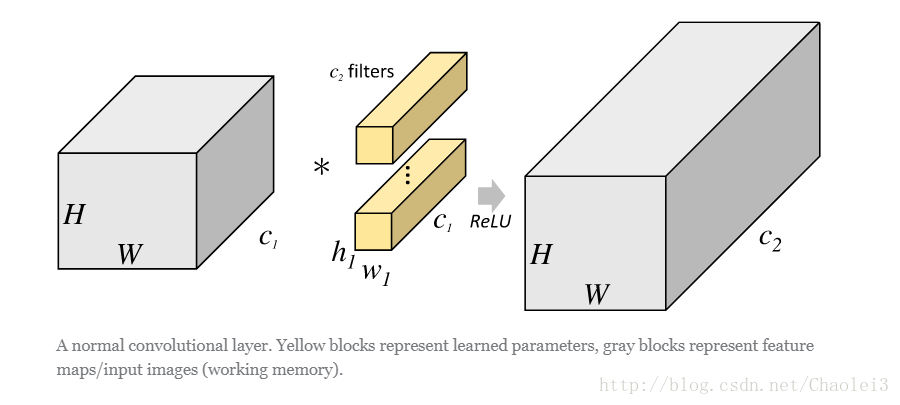
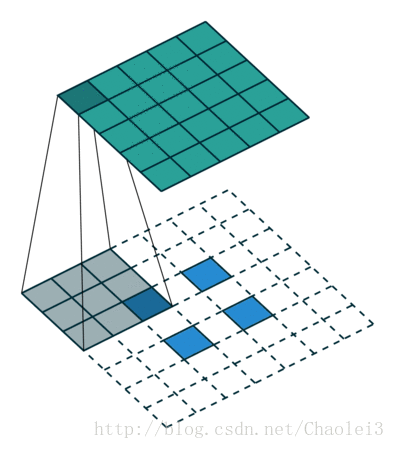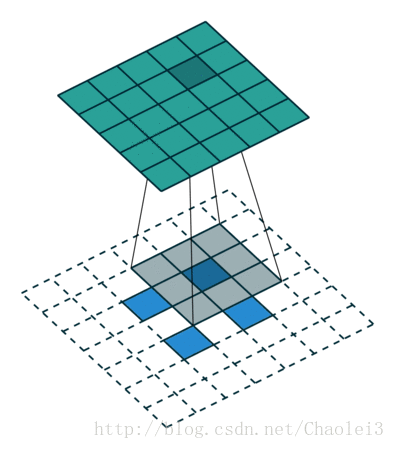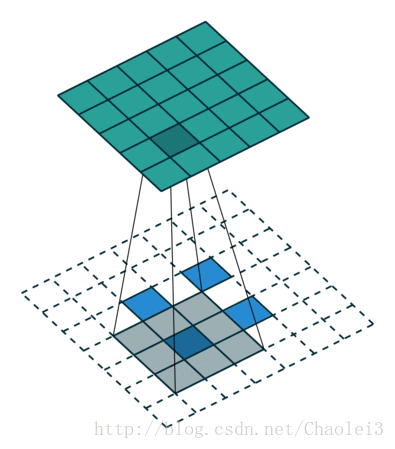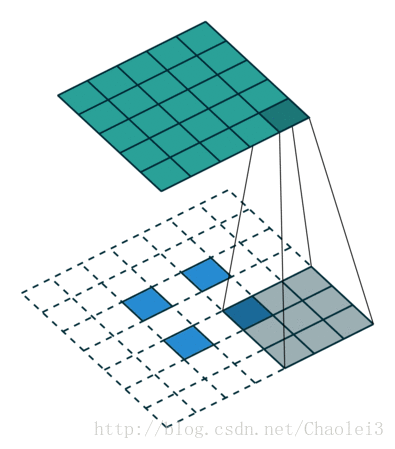
在說明分組卷積之前我們用一張圖來體會一下一般的卷積操作。
從上圖可以看出,一般的卷積會對輸入資料的整體一起做卷積操作,即輸入資料:H1×W1×C1;而卷積核大小為h1×w1,一共有C2個,然後卷積得到的輸出資料就是H2×W2×C2。這裡我們假設輸出和輸出的解析度是不變的。主要看這個過程是一氣呵成的,這對於儲存器的容量提出了更高的要求。
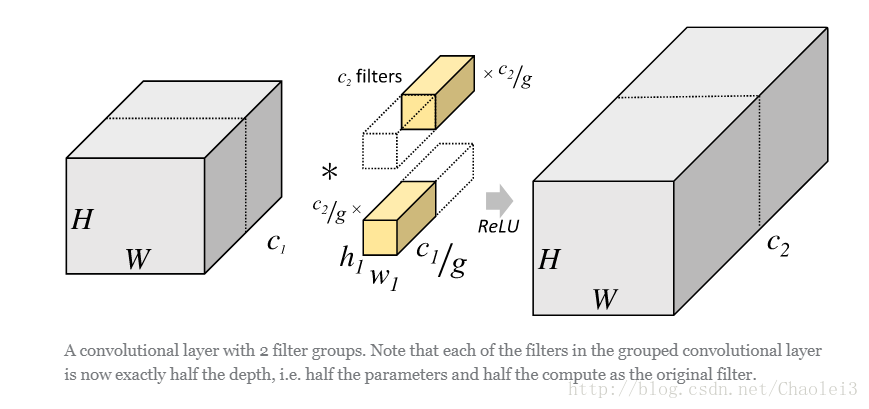
但是分組卷積明顯就沒有那麼多的引數。先用圖片直觀地感受一下分組卷積的過程。對於上面所說的同樣的一個問題,分組卷積就如下圖所示。
可以看到,圖中將輸入資料分成了2組(組數為g),需要注意的是,這種分組只是在深度上進行劃分,即某幾個通道編為一組,這個具體的數量由(C1/g)決定。因為輸出資料的改變,相應的,卷積核也需要做出同樣的改變。即每組中卷積核的深度也就變成了(C1/g),而卷積核的大小是不需要改變的,此時每組的卷積核的個數就變成了(C2/g)個,而不是原來的C2了。然後用每組的卷積核同它們對應組內的輸入資料卷積,得到了輸出資料以後,再用concatenate的方式組合起來,最終的輸出資料的通道仍舊是C2。也就是說,分組數g決定以後,那麼我們將並行的運算g個相同的卷積過程,每個過程裡(每組),輸入資料為H1×W1×C1/g,卷積核大小為h1×w1×C1/g,一共有C2/g個,輸出資料為H2×W2×C2/g。
2.2 分組卷積具體的例子
從一個具體的例子來看,Group conv本身就極大地減少了引數。比如當輸入通道為256,輸出通道也為256,kernel size為3×3,不做Group conv引數為256×3×3×256。實施分組卷積時,若group為8,每個group的input channel和output channel均為32,引數為8×32×3×3×32,是原來的八分之一。而Group conv最後每一組輸出的feature maps應該是以concatenate的方式組合。
Alex認為group conv的方式能夠增加 filter之間的對角相關性,而且能夠減少訓練引數,不容易過擬合,這類似於正則的效果。
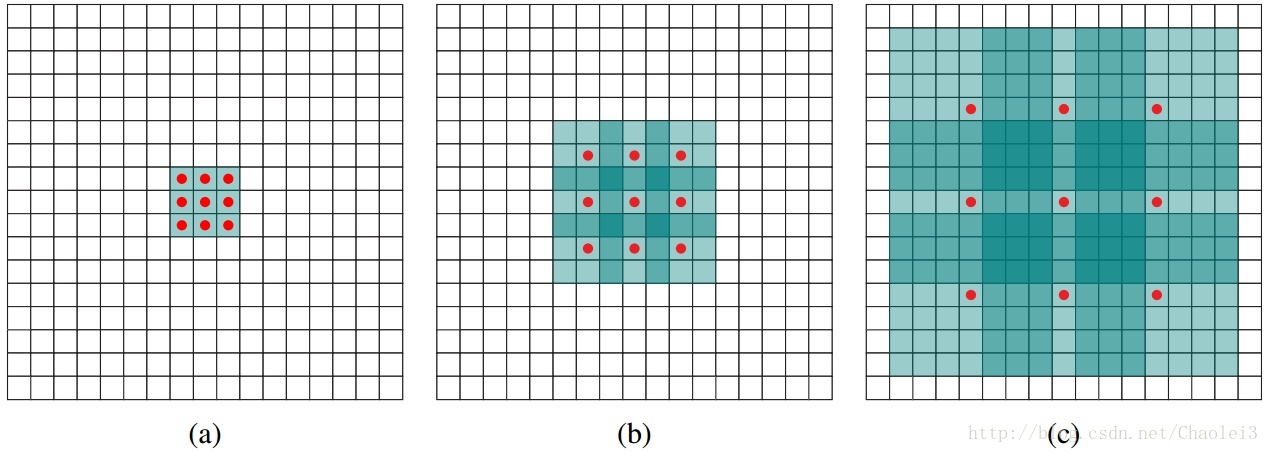
3 空洞(擴張)卷積(Dilated/Atrous Convolution)
空洞卷積(dilated convolution)是針對影象語義分割問題中下采樣會降低影象解析度、丟失資訊而提出的一種卷積思路。利用新增空洞擴大感受野,讓原本3 x3的卷積核,在相同引數量和計算量下擁有5x5(dilated rate =2)或者更大的感受野,從而無需下采樣。擴張卷積(dilated convolutions)又名空洞卷積(atrous convolutions),向卷積層引入了一個稱為 “擴張率(dilation rate)”的新引數,該引數定義了卷積核處理資料時各值的間距。換句話說,相比原來的標準卷積,擴張卷積(dilated convolution) 多了一個hyper-parameter(超引數)稱之為dilation rate(擴張率),指的是kernel各點之前的間隔數量,【正常的convolution 的 dilatation rate為 1】。
圖說空洞卷積的概念
(a)圖對應3x3的1-dilated conv,和普通的卷積操作一樣。(b)圖對應3x3的2-dilated conv,實際的卷積kernel size還是3x3,但是空洞為1,需要注意的是空洞的位置全填進去0,填入0之後再卷積即可。【此變化見下圖】(c)圖是4-dilated conv操作。
在上圖中擴張卷積的感受野可以由以下公式計算得到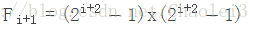
空洞卷積的動態過程
在二維影象上直觀地感受一下擴張卷積的過程:
上圖是一個擴張率為2的3×3卷積核,感受野與5×5的卷積核相同,而且僅需要9個引數。你可以把它想象成一個5×5的卷積核,每隔一行或一列刪除一行或一列。
在相同的計算條件下,空洞卷積提供了更大的感受野。空洞卷積經常用在實時影象分割中。當網路層需要較大的感受野,但計算資源有限而無法提高卷積核數量或大小時,可以考慮空洞卷積。
Dilated Convolution感受野指數級增長
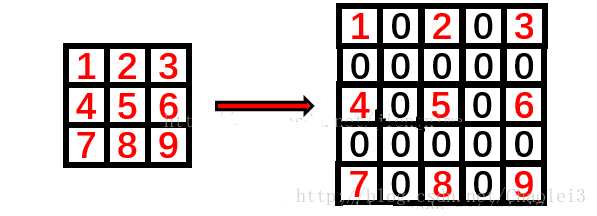
對於標準卷積核情況,比如用3×3卷積核連續卷積2次,在第3層中得到1個Feature點,那麼第3層這個Feature點換算回第1層覆蓋了多少個Feature點呢?
第3層:
第2層:
第1層:
第一層的一個5×5大小的區域經過2次3×3的標準卷積之後,變成了一個點。也就是說從size上來講,2層3*3卷積轉換相當於1層5*5卷積。題外話,從以上圖的演化也可以看出,一個5×5的卷積核是可以由2次連續的3×3的卷積代替。
但對於dilated=2,3*3的擴張卷積核呢?
第3層的一個點:
第2層:
可以看到第一層13×13的區域,經過2次3×3的擴張卷積之後,變成了一個點。即從size上來講,連續2層的3×3空洞卷積轉換相當於1層13×13卷積。
轉置卷積
轉置卷積(transposed Convolutions)又名反捲積(deconvolution)或是分數步長卷積(fractially straced convolutions)。反捲積(Transposed Convolution, Fractionally Strided Convolution or Deconvolution)的概念第一次出現是Zeiler在2010年發表的論文Deconvolutional networks中。
轉置卷積和反捲積的區別
那什麼是反捲積?從字面上理解就是卷積的逆過程。值得注意的反捲積雖然存在,但是在深度學習中並不常用。而轉置卷積雖然又名反捲積,卻不是真正意義上的反捲積。因為根據反捲積的數學含義,通過反捲積可以將通過卷積的輸出訊號,完全還原輸入訊號。而事實是,轉置卷積只能還原shape大小,而不能還原value。你可以理解成,至少在數值方面上,轉置卷積不能實現卷積操作的逆過程。所以說轉置卷積與真正的反捲積有點相似,因為兩者產生了相同的空間解析度。但是又名反捲積(deconvolutions)的這種叫法是不合適的,因為它不符合反捲積的概念。
轉置卷積的動態圖
△卷積核為3×3、步幅為2和無邊界擴充的二維轉置卷積
需要注意的是,轉置前後padding,stride仍然是卷積過程指定的數值,不會改變。
例子
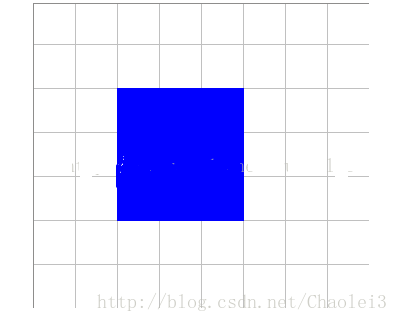
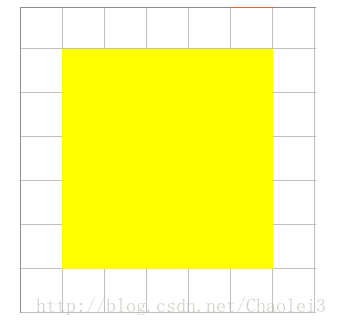
由於上面只是理論的說明了轉置卷積的目的,而並沒有說明如何由卷積之後的輸出重建輸入。下面我們通過一個例子來說明感受下。 比如有輸入資料:3×3,Reshape之後,為A :1×9,B(可以理解為濾波器):9×4(Toeplitz matrix) 那麼A*B=C:1×4;Reshape C=2×2。所以,通過B 卷積,我們從輸入資料由shape=3×3變成了shape=2×2。反過來。當我們把卷積的結果拿來做輸入,此時A:2×2,reshape之後為1×4,B的轉置為4×9,那麼A*B=C=1×9,注意此時求得的C,我們就認為它是卷積之前的輸入了,雖然存在偏差。然後reshape為3×3。所以,通過B的轉置 - “反捲積”,我們從卷積結果shape=2×2得到了shape=3×3,重建了解析度。
也就是輸入feature map A=[3,3]經過了卷積B=[2,2] 輸出為 [2,2] ,其中padding=0,stride=1,反捲積(轉置卷積)則是輸入feature map A=[2,2],經過了反捲積濾波B=[2,2].輸出為[3,3]。其中padding=0,stride=1不變。那麼[2,2]的卷積核(濾波器)是怎麼轉化為[4,9]或者[9,4]的呢?通過Toeplitz matrix。
至於這其中Toeplitz matrix是個什麼東西,此處限於篇幅就不再介紹了。但即使不知道這個矩陣,轉置卷積的具體工作也應該能夠明白的。