js math atan2
阿新 • • 發佈:2017-06-24
利用 傾斜 判斷 弧度 高度 例如 處理 wikipedia 連線
在雙十二活動中,視覺要求實現一個鼠標跟隨運動的的效果,就像“覺”的那個效果類似
其實原理很簡單,看鼠標從哪個方向進的及從哪個方向出的,然後區塊裏絕對定位的浮層就可以根據鼠標方向
運動;
如:在鼠標進入事件中判斷鼠標從左邊進入區塊那麽定位層就從left:區塊寬走到區塊零,在鼠標離開事件中判斷鼠標是從上邊離開的那麽定位層就從top:零走到負的區塊高度就可以的。是不是很簡單呢,但是有一個問題就是怎麽判斷方向?那麽我們的atan2就隆重出場了。
看一下w3cshool上是怎麽介紹atan2()的
atan2(x,y):返回-PI 到 PI 之間的值,是從 X 軸正向逆時針旋轉到點 (x,y) 時經過的角度。
看維基網上的一張圖:

那我們是不是計算出區塊四個頂點的的atan2值,然和鼠標的atan2值比較確定範圍看圖:
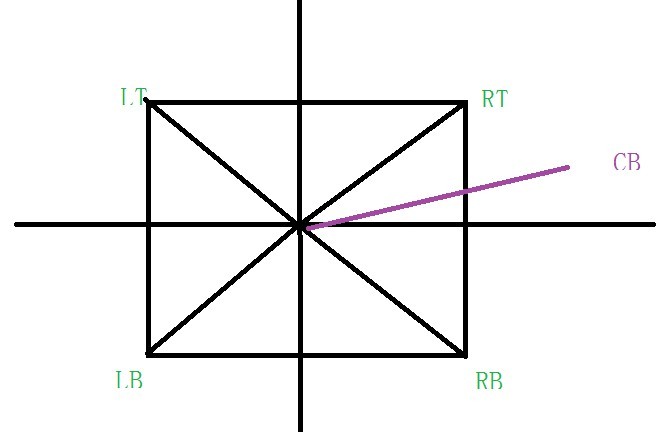
是不由
CB>=RB&&CB<RT就在左邊
CB>=RT&&CB<LT就在上邊
CB>=LB&&CB<RB就在下邊
否則就在右邊
| 我們可以使用正切操作將角度轉變為斜率,那麽怎樣利用斜率來轉換為角度呢?可以利用斜率的反正切函數將他轉換為相應的角度.as中有兩個函數可以計算反正切,我們來看一下. 1、as中Math.atan() Math.atan()接受一個參數:用法如下: angel=Math.atan(slope) angel為一個角度的弧度值,slope為直線的斜率,是一個數字,這個數字可以是負的無窮大到正無窮大之間的任何一個值. 不過,利用他進行計算比較復雜.因為他的周期性,一個數字的反正切值不止一個.例如atan(-1)的值可能是45度,也可能是225度.這樣就是他的周期性,對於正切函數來說,他的周期是180度,所以兩個相差180度的角具有相同的正切和斜率: tanθ=tan(θ+180) 然而,Math.atan()只能返回一個角度值,因此確定他的角度非常的復雜,而且,90度和270度的正切是無窮大,因為除數為零,我們也是比較難以處理的~!因此我們更多的會采用第二個函數. 2、Math.atan2() Math.atan2()接受兩個參數x和y,方法如下: angel=Math.atan2(y,x) x 指定點的 x 坐標的數字。 y 指定點的 y 坐標的數字。 計算出來的結果angel是一個弧度值,也可以表示相對直角三角形對角的角,其中 x 是臨邊邊長,而 y 是對邊邊長。 下面我們來測試一下這兩個函數: x=Math.atan(1)//計算正切值為1的數字對應的弧度值 trace(x) //輸出一個弧度值0.785398163397448 x=180*x/Math.PI//轉換為角度值 trace(x) //輸出45 x=Math.atan2(7,7) trace(x)//輸出0.785398163397448 x=180*x/Math.PI//轉換為角度值 trace(x)//輸出45 x=Math.atan2(7,-7) trace(x)2.35619449019234 x=180*x/Math.PI//轉換為角度值 trace(x)135 x=Math.atan2(-7,7) trace(x)//輸出-0.785398163397448 x=180*x/Math.PI//轉換為角度值 trace(x)//輸出-45 x=Math.atan2(-7,-7) trace(x)//輸出-2.35619449019234 x=180*x/Math.PI//轉換為角度值 trace(x)//輸出-135 //從這些測試可以看出,通過坐標系的自動調整,我們可以很自由的計算出處於不同象限的位置相對應的角度. 3、計算兩點間連線的傾斜角. 這種方法非常的有用. Math.atan2()函數返回點(x,y)和原點(0,0)之間直線的傾斜角.那麽如何計算任意兩點間直線的傾斜角呢?只需要將兩點x,y坐標分別相減得到一個新的點(x2-x1,y2-y1).然後利用他求出角度就可以了.使用下面的一個轉換可以實現計算出兩點間連線的夾角. Math.atan2(y2-y1,x2-x1) 不過這樣我們得到的是一個弧度值,在一般情況下我們需要把它轉換為一個角度. 下面我們用一段代碼來測試一下這樣的轉換. //測試,計算點(3,3)和(5,5)構成的連線的夾角 x=Math.atan2(5-3,5-3) trace(x)//輸出0.785398163397448 x=x*180/Math.PI//轉換為角度 trace(x)//輸出45 |
js math atan2
