基本數據結構(算法導論)與python
原文鏈接
Stack, Queue
Stack是後進先出, LIFO, 隊列為先進先出, FIFO
在Python中兩者, 都可以簡單的用list實現,
進, 用append()
出, Stack用pop(), Queue用pop(0), pop的時候註意判斷len(l)
對於優先隊列, 要用到前面講到的堆
鏈表和多重數組
這些數據結構在python中就沒有存在的價值, 用list都能輕松實現
散列表
為了滿足實時查詢的需求而產生的數據結構, 查詢復雜度的期望是O(1), 最差為O(n)
問題描述, 對於n個(key, value)對, 怎樣存儲可以在O(1)的時間復雜度內獲取特定key所對應的value. 這個問題裏, key默認是int, 當然key可以是字符串或其他, 那就想辦法把key轉換成int.
最簡單的方法是直接尋址表 , 就是創建和key空間一樣大小的數組A, 把value存儲到數組A[key]中.
這個方法簡單, 對應key空間不大的情況也可以用, 但是當key空間很大時, 這個太耗內存了, 而且沒有必要, 比如只有10個範圍在1到1000000的key, 你要分配個那麽大的數組, 明顯不合適
散列方法 , 自然想到我們應該用一個較小的數組來存儲, 那麽就需要把key空間範圍中的數字映射到較小所存儲空間上來. 這個映射的方法, 稱為散列函數 . 散列函數的選擇是很關鍵的, 而且這個沒有絕對的好壞, 每個散列函數都有它的適用範圍.
常用的散列函數如下, 將關鍵字k映射到m個槽
除法散列法, h(k) = k mod m
乘法散列法, h(k) = |m(KA mod 1)|, 0 全域散列, 想法就是準備一組散列函數, 每次使用時隨機選擇一個, 來克服散列函數的局限性. 比如定義散列函數組,h(k) = ((ak+b) mod p)mod m, p是足夠大的質數, 隨機選擇不同的a,b產生不同的散列函數
那麽把一個大的數字空間映射到一個較小的數字空間上, 那麽肯定會有重復, 這是不可避免的, 這種重復稱為碰撞 (collision).
有碰撞就要想辦法解決, 最簡單的想法, 就是鏈接法 .
理想狀態每個槽裏面只放一個key, 那麽search肯定是O(1)的, 直接就找到. 但是重復是不可避免, 如果有多個key被分配到同一個槽, 怎麽辦
那麽在槽中存放一個key的鏈表來存儲多個key, 這樣search肯定大於O(1), 最差的情況為O(n). 平均為O(1+a), a為裝載因子(load factor), 一個槽中平均存儲的元素數.
所以我們應該盡量減少碰撞的可能性, 最直接的方法是減少裝載因子
另一種解決碰撞的方法就是開放尋址法 , 做法是出現碰撞時, 根據規則探測另一個槽存放該元素
這個方法的好處就是沒有用鏈表, 不用指針, 節省的空間可以提供更多的槽, 壞處是數據可能會溢出, 所以要確保裝載因子不能大於1
現在的問題就是當發生碰撞時, 怎麽樣去探測下一個槽?
線性探測, h(k,i)=(h‘(k)+i) mod m,i=0,1,……,m-1, 這個方法會有個問題, 一次集群, 連續被占用的槽會不斷增加, 那麽後面偵測的時間會變長
二次探測, h(k,i)=(h‘(k)+c1*i+c2*i2 ) mod m, 這樣不用一個個連續去探測, 因為有個平方, 會隔的遠些, 但還是會有二次集群, 因為初始探測決定了整個探測序列
雙重哈希 , h(k,i)=(h1(k)+i*h2(k)) mod m, 這時現在最好的探測方法
開放尋址法search復雜度為O(1/(1-a)), a為裝載因子
止於至善, 有沒有一種方法可以在最差情況下也能達到O(1), 理論上是有的, 但必須是輸入數據為靜態數據, 方法叫perfect hashing, 完美散列
思路也不復雜, 采用兩級hash, 一級類似於鏈接法, 采用全域散列把n個輸入劃分到m個槽內, 然後在每個槽內進行二級散列, 並確保二級散列是無沖突的.
可以證明當, m = n2 時, 出現沖突的概率小於0.5, 所以只要保證一級散列函數選取合適, 可以均勻的把n個元素分布到m個槽中, 並保證槽中二級散列的空間足夠大, 就可以達到效果.
在python中, 無需自己實現散列表, 用dict就可以
二叉查找樹
二叉查找樹, 也是一種便於查找的數據結構, 任意一個樹節點的左子樹都小於該節點, 右子樹都大於該節點. 隨機構造的二叉樹, 理想樹高為logn, 其上操作的平均復雜度為O(logn)
既然前面的Hash可以提供O(1)的search, 為什麽還需要這個數據結構了, 他更靈活, 他可以提供除search外的其他操作, 如Minimum, Maximum, Predecessor, Successor, Insert等操作.
他可以用於字典, 或優先隊列, 可是如果字典, 我首選Hash, 優先隊列, 我首選堆, 沒有想到非要用二叉樹的例子, 往往是二叉樹的變種更有實用價值.
二叉樹最大的問題, 是構造順序不能保證是隨機的, 就是說不能保證二叉樹是平衡的, 不平衡就麻煩了, 極限情況是個單鏈表. 常用的一種平衡二叉樹, 為紅黑樹.
B樹也是二叉樹很有用的變種, 常用於創建數據庫索引, 後面會具體討論.
下面給出python實現
 1 class Node:
1 class Node:2
3 def __init__(self,data):
4 self.left = None
5 self.right = None
6 self.parent = None
7 self.data = data
8
9 def insert(self, data):
10 # #recursion version
11 # if data < self.data:
12 # if self.left:
13 # self.left.insert(data)
14 # else:
15 # self.left = self.createNode(data)
16 # self.left.parent = self
17 # else:
18 # if self.right:
19 # self.right.insert(data)
20 # else:
21 # self.right = self.createNode(data)
22 # self.right.parent = self
23 #non-recursion version
24 node = self
25 while node:
26 if data < node.data:
27 next = node.left
28 else:
29 next = node.right
30 if next:
31 node = next
32 else:
33 break
34 nn = self.createNode(data)
35 if data < node.data:
36 node.left = nn
37 node.left.parent = node
38 else:
39 node.right = nn
40 node.right.parent = node
41 return nn
42
43 def createNode(self, data):
44 return Node(data)
45
46 def printTree (self):
47 """中序遍歷"""
48 if self.left:
49 self.left.printTree()
50 print self.data
51 if self.right:
52 self.right.printTree()
53
54 def maxNode(self):
55 if self.right:
56 return self.right.maxNode()
57 else:
58 return self
59
60 def minNode (self):
61 if self.left:
62 return self.left.maxNode()
63 else:
64 return self
65
66 def lookup(self, data):
67 if self.data == data:
68 return self
69
70 if self.data > data:
71 if self.left:
72 return self.left.lookup(data)
73 else:
74 return None
75 else:
76 if self.right:
77 return self.right.lookup(data)
78 else:
79 return None
80
81 def successor(self):
82 """
83 有右子樹時,很容易理解, 取右子樹的最小值
84 沒有右子樹時, 也就是說該節點是當前子樹的最大節點, 該節點的後繼為把該子樹作為左子樹的最近的根節點
85 如果要取前驅, 道理一樣
86 """
87 n= self
88 if n.right:
89 return n.right.minNode()
90 else:
91 p = n.parent
92 while p and p.right == n:
93 n = p
94 p = p.parent
95 return p
96
97 def delete(self, root):
98 """
99 對於沒有子樹,或只有一個子樹, 都很好處理
100 如果有兩個子樹, 做法是把節點後繼節點拷貝到當前節點, 然後刪除後繼節點
101 這不是唯一的做法, 但這樣做對樹原有的平衡性破壞最小
102 當root被刪除時, root會變, 所以需要返回新的root
103 """
104 n= self
105
106 if n.left and n.right:
107 s = n.right.minNode()
108 n.data = s.data
109 root = s.delete(root)
110 return root
111
112 #特殊處理根節點
113 if not n.parent:
114 if n.left:
115 root = n.left
116 n.left = None
117 root.parent = None
118 elif n.right:
119 root = n.right
120 n.right = None
121 root.parent = None
122 else:
123 root = None
124
125 return root
126
127 if not n.left and not n.right:
128 if n.parent.left == n:
129 n.parent.left = None
130 else:
131 n.parent.right = None
132 else:
133 if n.parent.left == n:
134 n.parent.left = n.left or n.right
135 else:
136 n.parent.right = n.left or n.right
137 n.parent = None
138 return root
139 def buildTree():
140 root = Node(8)
141 root.insert(3)
142 root.insert(10)
143 root.insert(1)
144 root.insert(6)
145 root.insert(4)
146 root.insert(7)
147 root.insert(14)
148 root.insert(13)
149 root.printTree()

紅黑樹
前面說了, 二叉查找樹最大的問題就是平衡性, 而紅黑樹就很好的解決了這個問題, 什麽是紅黑樹
1)每個結點要麽是紅的,要麽是黑的。
2)根結點是黑的。
3)每個葉結點,即空結點(NIL)是黑的。
4)如果一個結點是紅的,那麽它的倆個兒子都是黑的。
5)對每個結點,從該結點到其子孫結點的所有路徑上包含相同數目的黑結點。
滿足上面幾點就叫做紅黑樹, 坦白的講, 這個數據結構真是有夠復雜的, 對於能想出這樣方法的NB, 崇拜之情如滔滔江水
這個樹有什麽, 明顯就是比較平衡, 因為根到葉的最長距離最多是最短距離的2倍, 為什麽?
因為黑高(包含的黑節點數)都是一樣的, 所以最短路徑就是全黑, 最長路徑為紅黑交替, 所以最長最多是最短2倍.
可以證明紅黑樹的高度至多為2lg(n+1), 樹的操作復雜度完全取決於樹高, 這就很好的解決了二叉樹的不平衡問題.
紅黑樹比較有特色的操作為旋轉(pivot) ,
紅黑樹的插入操作
對於紅黑樹的插入, 默認插入節點為紅節點, 必須是紅的, 根是黑的, 如果插黑的, 就和二叉樹沒有區別了. 而且插紅的不會打破黑高相同規則5), 只會打破規則2), 4), 所以只需要針對這兩個規則進行rebalance. 拋開rebalance不談, 紅黑樹的插入操作和二叉樹相同的, 但是關鍵就是插完後的rebalance過程來保證紅黑樹的規則.
rebalance的過程是比較復雜的, 不過我們可以case by case的分析, 總的來說只有兩種操作, 旋轉 和變色 , 並且只有出現連續兩個黑色節點時才需要旋轉.
1) 插入的是根結點,直接把此結點變為黑色
2) 插入的結點的父結點是黑色, 很好什麽也不用做
3) 當前結點的父結點是紅色且祖父結點的另一個子結點(叔叔結點)是紅色
父節點紅色, 打破了規則4), 而且可以推斷祖父肯定是黑的, 並且叔叔結點是紅色, 說明這個子樹是平衡的(黑紅相間), 不需要旋轉.
既然不旋轉就變色, 父節點和叔叔節點變黑,祖父結點變紅,那這樣祖父節點就有可能違反規則, 所以繼續對祖父節點進行rebalance
4)當前節點的父節點是紅色,叔叔節點是黑色
這種情況比較復雜, 因為祖父肯定是黑的, 叔叔節點也是黑的, 所以出現連續兩個黑色節點, 樹不平衡, 肯定需要旋轉, 怎麽個旋轉法?
首先要看叔叔節點是祖父節點的左節點, 還是右節點, 這個決定了旋轉的方向, 我們只需要討論其中一種情況, 另一種情況就是往相反的方向旋轉就可以了
我們就討論一下叔叔節點是祖父節點的右節點的情況, 就是父節點為祖父節點的左節點, 這兒根據當前節點位置又分為兩種情況,
a)當前節點為父節點的右節點, 以父節點左旋, 並把父節點作為當前節點
b)當前節點為父節點的左節點, 以祖父節點右旋, 並改變父節點, 祖父節點顏色
大家想一下, 這種情況下旋轉的目的是因為在祖父節點的右子樹上連續出現兩個黑節點, 所以我們最終需要通過一次右旋來增加右子樹的高度, 就如b)情況所示, 通過一次右旋, 並改色, 達到了恢復紅黑樹的所有規則.
但對於a), 你可以試著直接右旋, 你沒法改色來滿足紅黑樹的規則, 所以要先通過一次左旋來達到b), 進而進行右旋, 所以a)只是一個中間步驟.
好了, 這邊分析完叔叔節點是祖父節點的右節點的情況, 對於叔叔節點是祖父節點的左節點的情況, 類似想想也能明白.
紅黑樹的刪除操作
回想一下前面二叉樹的刪除操作, 如果需要刪除的節點有兩個兒子,那麽問題可以被轉化成刪除另一個只有一個兒子的節點的問題 (這裏的兒子,為非葉子節點的兒子,紅黑樹中leaf節點都是Null節點)。為什麽?因為這兒的刪除操作過程, 是找到該節點的後繼, copy到當前節點, 然後刪除後繼(右子樹中最小節點),此時的後繼節點最多只有一個兒子(並且是右兒子),否則就不是後繼。
所以問題簡化為,我們只需要討論刪除只有一個兒子的節點 (如果它兩個兒子都為空,即均為葉子,我們任意將其中一個看作它的兒子),到這兒我們就把一個看似復雜的問題轉化為相對簡單的問題。
在刪除這個節點時,根據顏色不同,分為3種情況,
1)該節點為紅色,這種情況一定沒有兒子,直接刪除沒有任何影響
2)該節點為黑色,如果有兒子一定是有且只有一個紅色的兒子,這個也好辦,把紅色的兒子替換改節點, 並改為黑色。
3)該節點為黑色,且沒有兒子,即只有兩個葉子,這個問題就比較復雜了,你直接刪除這個節點, 破壞了規則5),這個分支明顯比其他黑高少1.
現在就對上面情況3)具體分析,思路是什麽,明顯直接從該節點上沒法解決問題,他被幹掉了,他也沒有兒子,那就找他父親,兄弟吧,總要有人負責的嗎, 如果他沒有父親了,孤兒, 他就是根節點, 他被幹掉, 樹都沒了,當然不用做啥了。而且如果有父親,他就一定有兄弟,不流行只生一個。
那麽就把他的父節點,兄弟節點一起考慮進來,形成一個子樹來解決這個問題。怎麽解決? 那麽我就來談談我的理解,
攘外必先安內,第一步我們首先保證這個子樹內部是滿足紅黑樹規則的(我們假設被刪除的節點在左子樹, 在右子樹一樣處理, 只是旋轉方向相反)
現在的情況時被刪除子樹的黑高比他的兄弟子樹黑高少1, 怎麽辦?
a)最簡單的是, 把兄弟節點改紅, 這樣讓他的黑高也減1
這種改法必須滿足的條件是, 兄弟節點首先是黑的, 而且他的子節點也都是黑的(Case 2 ), 這樣可以直接把兄弟節點由黑改紅, 在不破壞其他規則的前提下, 使兩個子樹黑高相同.
但是你不能保證這種case一定出現, 其他情況如下,
b)兄弟節點是紅的, 這種情況下, 兄弟節點一定是兩個黑色子節點(Case1 ). 這種情況下, 通過對父節點的一次左旋並改色, 就能夠滿足(Case 2)的條件.
c)兄弟節點是黑的, 但兄弟節點的子節點至少有一個是紅色的. 這樣你也沒法直接改兄弟節點的顏色, 改了就和紅子節點矛盾了.
c1)如果兄弟節點的右兒子SR 是紅色的(Case4 ), 做法是把父節點做一次左旋, 並把父節點和都改成SR 黑色 , 這樣左右子樹的黑高就相同了.
c2)如果兄弟節點只有左兒子SL 是紅色的(Case3 ), 無法直接按c1處理, 因為通過左旋把右子樹挪了一個黑節點, 到左子樹, 但右子樹沒有可以改黑的紅節點, 導致右子樹黑高少1.
所以需要通過對兄弟節點S進行一次右旋, 並改色, 就可以滿足(Case 4 )的條件.
第二步, 現在子樹內部黑高已經平衡, 但對於整個紅黑樹而言, 黑高是否平衡?
可以看到對於c)而言, 子樹內的黑高不增不減, 對全局沒有影響
但對於a)b)而言, 為了平衡內部黑高, 子樹的黑高整個減少1 (Case 2 )
如果子樹的根結點為紅, 把它變黑就可以解決這個問題(紅黑樹中, 節點變黑比較方便只需考慮黑高, 變紅比較麻煩)
如果子樹根節點為黑, 這就相當於, 把我們剛解決的問題(子樹黑高少1), 往上(朝根節點方向)提升了一層, 遞歸去解決. 如果這個問題一直無法解決, 最終會提升到根節點的位置, 這時這個問題就不用解決了, 相當於把整個紅黑樹的黑高都減了1, 這樣也平衡了.
有了上面的理解再去看Wiki或算法導論具體的算法就比較容易了, 個兒覺得它們對於刪除解釋的不夠清楚, 而且圖畫的比較讓人困惑, 比如你看看(Case1 )的圖, 對於左圖是刪除後的情況, 要轉化為右圖, 你看看左圖有黑高不平衡嗎, 明顯是平衡的嗎, 那還做什麽? 對於N而言, 要麽是葉節點, 要麽是一棵子樹, 他的黑高應該和3,4,5,6節點(或子樹)一致的, 你說這個圖畫的怪不怪, 誤導性很強, 只能大概示意, 不過大家都用這個圖, 我也就不改了.
1)兄弟S 是紅色。
在這種情況下我們在N的父親上做左旋轉 ,把紅色兄弟轉換成N的祖父。我們接著對調 N 的父親和祖父的顏色。
2)兄弟S 和 S 的兒子都是黑色的
下面兩種情況的區別僅僅是子樹根節點的顏色不同, 上面已經解釋過了.
在這種情況下,我們簡單的重繪 S 為紅色。結果是通過S的所有路徑,它們就是以前不 通過 N 的那些路徑,都少了一個黑色節點。因為刪除 N 的初始的父親使通過 N 的所有路徑少了一個黑色節點,這使事情都平衡了起來。但是,通過 P 的所有路徑現在比不通過 P 的路徑少了一個黑色節點,所以仍然違反屬性4。要修正這個問題,我們要從情況 1 開始,在 P 上做重新平衡處理。
S 和 S 的兒子都是黑色,但是 N 的父親是紅色。在這種情況下,我們簡單的交換 N 的兄弟和父親的顏色。這不影響不通過 N 的路徑的黑色節點的數目,但是它在通過 N 的路徑上對黑色節點數目增加了一,添補了在這些路徑上刪除的黑色節點。
3)S 是黑色,S 的左兒子是紅色,S 的右兒子是黑色,而 N 是它父親的左兒子。在這種情況下我們在 S 上做右旋轉,這樣 S 的左兒子成為 S 的父親和 N 的新兄弟。我們接著交換 S 和它的新父親的顏色。
4)S 是黑色,S 的右兒子是紅色,而 N 是它父親的左兒子。在這種情況下我們在 N 的父親上做左旋轉,這樣 S 成為 N 的父親和 S 的右兒子的父親。我們接著交換 N 的父親和 S 的顏色,並使 S 的右兒子為黑色。
下面給出紅黑樹的python實現, 刪除沒寫, 以後有空補
 1 class RBTreeNode(Node):
1 class RBTreeNode(Node):2 """ red-black tree node"""
3 def __init__(self, data):
4 Node.__init__(self, data)
5 self.color = ‘red‘
6
7 def createNode(self, data):
8 return RBTreeNode(data)
9
10 def pivotLeft(self):
11 """ """
12 p = self.parent
13 l = self.left
14 r = self.right
15 #if has right child, save the left child of it
16 if r:
17 rl= r.left
18 else:
19 return
20 #after left pivot, r become new root of the child tree, so update r.parent
21 if p:
22 if p.left == self:
23 p.left = r
24 else:
25 p.right = r
26 r.parent = p
27 else:
28 r.parent = None
29 # update r.left, r.right not change
30 r.left = self
31 #update self.parent and self.right, left not change
32 self.parent = r
33 self.right = rl
34
35 return self, r
36 def pivotRight(self):
37 """ same logic with pivotLeft, just exchange the r and l"""
38 p = self.parent
39 l = self.left
40 r = self.right
41 if l:
42 lr= l.right
43 else:
44 return
45 if p:
46 if p.left == self:
47 p.left = l
48 else:
49 p.right = l
50 l.parent = p
51 else:
52 l.parent = None
53 l.right = self
54 self.parent = l
55 self.left = lr
56 return self, l
57
58 def insert(self, data):
59 """"""
60 n = Node.insert(self, data)
61 print n.data
62 #rebalance for insert
63 n.rebalance()
64
65 def rebalance(self):
66 """"""
67 n = self
68 p = n.parent
69 if not p:
70 n.black()
71 return
72 g = p.parent
73 #parent is black, no problem
74 if p and p.isBlack(): return
75
76 u = g.getOtherChild(p)
77 #p is red, u is red, then g must be black
78 if p.isRed()and u and u.isRed():
79 p.black()
80 u.black()
81 g.red()
82 g.rebalance()
83
84 #p is red, but u isn‘t red, black or leaf
85 if p.isRed():
86 if n.isRight() and p.isLeft():
87 print ‘nr, pl‘
88 p.pivotLeft()
89 n, p = p, n
90 if n.isLeft() and p.isLeft():
91 print ‘nl, pl‘
92 p.black()
93 g.red()
94 g.pivotRight()
95 return
96
97 if n.isLeft() and p.isRight():
98 print ‘nl, pr‘
99 p.pivotRight()
100 n, p = p, n
101 if n.isRight() and p.isRight():
102 print ‘nr, pr‘
103 p.black()
104 g.red()
105 g.pivotLeft()
106 return
107
108
109 def isLeft(self):
110 n = self
111 p = self.parent
112 if p and n == p.left:
113 return True
114 else:
115 return False
116 def isRight(self):
117 n = self
118 p = self.parent
119 if p and n == p.right:
120 return True
121 else:
122 return False
123 def isBlack(self):
124 if self.color == ‘black‘:
125 return True
126 else:
127 return False
128 def isRed(self):
129 if self.color == ‘red‘:
130 return True
131 else:
132 return False
133 def black(self):
134 self.color = ‘black‘
135 def red(self):
136 self.color = ‘red‘
137
138 def getOtherChild(self,child):
139 """ Give one child, and return other child"""
140 if self.left == child:
141 return self.right
142 else:
143 return self.left
144
145 def Print(self, indent):
146 for i in range(indent):
147 print " ",
148 print "%s (%s)" % (self.data, self.color)
149 if not self.left:
150 for i in range(indent+1):
151 print " ",
152 print "None(Black)"
153 else:
154 self.left.Print(indent+1)
155 if not self.right:
156 for i in range(indent+1):
157 print " ",
158 print "None(Black)"
159 else:
160 self.right.Print(indent+1)
161
162 class RBTree:
163 """ red-black tree"""
164 def __init__(self):
165 self.root = None
166
167 def insert(self, data):
168 if self.root:
169 self.root.insert(data)
170 self.updateRoot()
171 else:
172 self.root = RBTreeNode(data)
173 self.root.color = ‘black‘
174
175 def updateRoot(self):
176 """Update root node when root changes"""
177 n = self.root.parent
178 while n:
179 if n.parent:
180 n = n.parent
181 else:
182 break
183 if n:
184 self.root = n
185
186 def Print(self):
187 if self.root == None:
188 print "Empty"
189 else:
190 self.root.Print(1)
191 def buildRBTree():
192 tree = RBTree()
193 for i in range(10):
194 tree.insert(i)
195 tree.Print()

圖
圖的表示和搜索
圖,G=(V,E) ,的表示兩種方法, 鄰接表和鄰接矩陣. 兩者各有利弊, 都可以適用於有向圖, 無向圖, 加權圖
鄰接表 , 最常用的表示方法, 適用於稀疏圖或比較小的圖, 空間復雜度為(V+E), 優點是簡單,空間耗費小, 缺點就是確定邊是否存在效率低
鄰接矩陣 , 用於稠密圖或需要迅速判斷兩點間邊存在的場景, 空間復雜度為(V2 ), 優點是判斷邊存在問題快, 缺點就是空間耗費比較大, 是一種用空間換時間的方法. 有些對空間的優化, 比如對於無向圖, 矩陣是對稱的, 所以只需要存儲一半. 對於非加權圖, 每個邊只需要用1bit存儲.
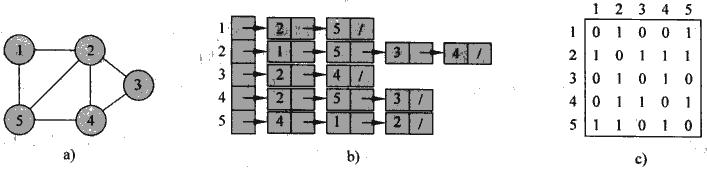
那麽用python怎麽表示圖, 沒有語言直接有圖這樣的數據結構, 不過對於python而言, 通過字典加上list可以很容易的表示圖(http://www.python.org/doc/essays/graphs.html), 例子如下
 1 #A -> B
1 #A -> B2 #A -> C
3 #B -> C
4 #B -> D
5 #C -> D
6 #D -> C
7 #E -> F
8 #F -> C
9 graph = {‘A‘: [‘B‘, ‘C‘],
10 ‘B‘: [‘C‘, ‘D‘],
11 ‘C‘: [‘D‘],
12 ‘D‘: [‘C‘],
13 ‘E‘: [‘F‘],
14 ‘F‘: [‘C‘]}

圖的搜索方法 分廣度優先 和深度優先 兩種, 這是最基本的圖算法, 也是圖算法的核心. 其他的圖算法一般都是基於圖搜索算法或是它的擴充.
廣度優先搜索 (breadth-first search)
廣度優先是最簡單的圖搜索算法之一, 也是許多重要的圖算法的原型. 在Prim最小生成樹算法和Dijkstra單源最短路徑算法中, 都采用了類似的思想.
顧名思義, 給定一個源頂點s, 廣度優先算法會沿其廣度方向向外擴展, 即先發現和s距離為k的所有頂點, 然後才發現和s距離為k+1的所有頂點.
顯然這樣的搜索方式, 按照節點被發現的順序, 最終會生成一棵樹, 稱之為廣度優先樹 , 每個節點至多被發現一次(第一次, 後面再遍歷到就不算了), 僅當節點被發現時, 他的前趨節點為他的父節點, 所以廣度優先樹又形式化的稱為該圖的前趨子圖 .
我們還可以證明, 在廣度優先樹, 任意節點到源頂點s的距離(樹高)為他們之間的最短距離 .
這個很容易證明, 假設在廣度優先樹上該節點n到s的距離為k, 而n到s的最短距離為k-1.
由於是廣度優先搜索, 必須要先發現和s距離為k-1的所有頂點, 然後才會去發現和s距離為k的頂點, 所以產生矛盾, 在廣度優先樹上距離應該是k-1, 而不可能是k, 從而得證這就是最短距離.
所以廣度優先算法可用於求圖中兩點間(a,b)的無權最短路徑. 方法首先以a為源求前趨子圖(即廣度優先樹), 然後在樹中找到b, 不斷求其前趨, 到a為止, 中間經過的節點就是其最短路徑. 如果無法達到a, 則a,b間不可達.
實現如下, 在實現BFS算法時, 我們需要用到queue數據結構, 來存放仍需繼續搜索的節點...
 1 def BFS(graph, start):
1 def BFS(graph, start):2 parent = {start:None}
3 dist = {start:0}
4 queue = [start]
5
6 while queue:
7 v = queue.pop(0)
8 print v
9 e = graph[v]
10 for n in e:
11 if not parent.get(n) and not dist.get(n):
12 parent[n] = v
13 dist[n]= dist[v]+1
14 queue.append(n)
15 print n, parent[n], dist[n]
16 return parent
17
18 def shortestPath(parent, start, end):
19 if start == end:
20 print start
21 return
22 p = parent.get(end)
23 if not p:
24 print ‘no path‘
25 return
26 shortestPath(parent, start, p)
27 print end
28 if __name__ == "__main__":
29 graph = {‘A‘: [‘B‘, ‘C‘,‘E‘],
30 ‘B‘: [‘A‘,‘C‘, ‘D‘],
31 ‘C‘: [‘D‘],
32 ‘D‘: [‘C‘],
33 ‘E‘: [‘F‘,‘D‘],
34 ‘F‘: [‘C‘]}
35 p = BFS(graph,‘A‘)
36 shortestPath(p, ‘A‘, ‘F‘)

深度優先搜索 (Depth-first search)
深度優先搜索所遵循的搜索策略是盡可能“深”地搜索圖。在深度優先搜索中,對於最新發現的頂點,如果它還有以此為起點而未探測到的邊,就沿此邊繼續漢下去。當結點v的所有邊都己被探尋過,搜索將回溯 到發現結點v有那條邊的始結點。這一過程一直進行到已發現從源結點可達的所有結點為止。
深度優先搜索所要回答的基本問題是"What parts of the graph are reachable from a given vertex?", 這其實就是歷史悠久的迷宮問題, 在入口點是否可以達到出口點, 這就是深度優先最基本的應用. 科學來源於生活, "Everybody knows that all you need to explore a labyrinth is a ball of string and a piece of chalk.", 對於迷宮我們必須有粉筆和線團 , 粉筆是用來標記走過的路, 防止陷入cycle, 線團是用來準確的回溯到上一個路口.
那麽怎麽用程序來模擬粉筆和線團來實現深度優先搜索, 粉筆很容易解決, 對每個節點用0/1來表示是否已訪問. 而線團就需要用stack來表示, push就是unwind, pop就是rewind, 是不是很有意思. 基於這個思路任何迷宮都是可解的. 而往往stack也是用隱形的方式來實現的, 通過函數遞歸. 我下面的實現即給出了遞歸函數的實現, 也給出了直接用stack的實現, 更清晰的看出chalk的使用方式.
 1 pre = {}
1 pre = {}2 post = {}
3 clock = 1
4 stack = []
5 def DFS(graph):
6 global pre
7 for v in graph.keys():
8 if not pre.get(v):
9 visit_stack(graph, v)
10
11 def visit(graph, v):
12 global pre
13 global post
14 global clock
15 pre[v] = clock
16 clock = clock + 1
17 print v, pre[v]
18 edges = graph[v]
19 for e in edges:
20 if not pre.get(e):
21 visit(graph, e)
22 post[v] = clock
23 clock = clock + 1
24 print v, pre[v], post[v]
25
26 def visit_stack(graph, v):
27 """
28 use stack to replace recursion
29 """
30 global pre
31 global post
32 global clock
33 global stack
34 stack.append(v)
35 while stack:
36 print stack
37 next = stack.pop()
38 print ‘pop:‘, next
39 while next:
40 if not pre.get(next):
41 pre[next] = clock
42 clock = clock + 1
43 print next, pre[next]
44 edges = graph.get(next)
45 vec = get_white_v(edges)
46 if vec:
47 print ‘push:‘, next
48 stack.append(next)
49 else:
50 post[next] = clock
51 clock = clock + 1
52 print next, pre[next], post[next]
53 next = vec
54
55 def get_white_v(edges):
56 global pre
57 for e in edges:
58 if not pre.get(e):
59 return e
60 return None

依據深度優先搜索可以獲得有關圖的結構的大量信息。深度優先搜索所要解決的基本問題是可達性問題, 即連通性問題, 通過這個算法, 我們可以輕松的找到所有連通子圖 , 對於每個子圖可以生成一個深度優先樹, 從而深度優先搜索最終產生的是深度優先森林 .
除此之外, 深度優先搜索還能得到的很重要的信息是, for each node, we will note down the times of two important events, the moment of first discovery (corresponding to previsit ) and that of final departure (postvisit ). 即在第一次發現該節點, 和完成該節點所有相鄰節點遍歷時, 記下兩個時間戳(如下圖).
然後基於previsit和postvisit, 就有一些有趣的推論,
1. 子樹的源點一定是previsit最小, 而postvisit最大, 因為是遞歸, 最先開始的最後完成.
2. 對於兩個節點u,v, 如果存在後裔和祖先的關系, 那麽祖先區間(pre(u),post(u))必定包含後裔區間(pre(v),post(v)). 如果u,v兩個區間沒有包含關系(完全分離的), 那就一定不存在後裔祖先關系.
3. 圖中的邊由此也可以分為幾類,
樹枝 (tree),是深度優先森林中的邊,如果結點v是在探尋邊(u,v)時第一次被發現,那麽邊(u,v)就是一個樹枝。
反向邊 (back),是深度優先樹中連結結點u到它的祖先v的那些邊,環也被認為是反向邊。
正向邊 (forward),是指深度優先樹中連接頂點u到它的後裔的非樹枝的邊。
交叉邊 (cross),是指所有其他類型的邊, 即兩個節點的區間完全分離.
這樣就可以引出深度優先搜索的第二個應用, 有向無環圖(Directed acyclic graphs, Dags)的拓撲排序問題
Dags are good for modeling relations like causalities(因果關系), hierarchies(層級關系), and temporal dependencies(時間依賴關系).
這個在日常生活中經常會碰到這樣的情況, 一堆事情之間有因果, 時間關系, 先做誰, 後做誰, 這個就是典型的拓撲排序問題.
下面的圖可以給出一個穿衣服的例子,
拓撲排序的實現很簡單, 有兩種思路,
1. 對圖完成深度優先搜索, 然後按節點的postvisit遞減排列就得到了拓撲排序.
2. 第二種思路不依賴於postvisit, 首先選擇一個無前驅的頂點(即入度為0的頂點,圖中至少應有一個這樣的頂點,否則肯定存在回路),然後從圖中移去該頂點以及由他發出的所有有向邊,如果圖中還存在無前驅的頂點,則重復上述操作,直到操作無法進行。如果圖不為空,說明圖中存在回路,無法進行拓撲排序;否則移出的頂點的順序就是對該圖的一個拓撲排序。
前面討論的無向圖的連通性, 對於有向圖的連通性問題, 更加復雜一點, 對於有向圖必須互相可達, 才認為是連通的.
在有向圖G中,如果任意兩個不同的頂點相互可達 ,則稱該有向圖是強連通 的。有向圖G的極大強連通子圖稱為G的強連通分支 。
把有向圖分解為強連通分支是深度優先搜索的一個經典應用實例. 很多有關有向圖的算法都從分解步驟開始,這種分解可把原始的問題分成數個子問題,其中每個子子問題對應一個強連通分支。構造強連通分支之間的聯系也就把子問題的解決方法聯系在一起,我們可以用一種稱之為分支圖的圖來表示這種構造, 而分支圖一定是dags.
通過深度優先搜索來把有向圖分解為強連通分支的方法也很簡單,
procedure Strongly_Connected_Components(G);
begin
1.調用DFS(G)以計算出每個結點u的完成時刻post[u];
2.計算出GT ;
3.調用DFS(GT ),但在DFS的主循環裏按針post[u]遞減的順序考慮各結點(和第一行中一樣計算);
4.輸出第3步中產生的深度優先森林中每棵樹的結點,作為各自獨立的強連通支。
end;
為什麽這樣就可以找到強連通分支, 從上面的圖可知, 圖與轉置圖的強連通分支是一樣的. 先對G完成DFS, 然後按post遞減的順序,
現在基於分支圖來考慮, 分支圖是dag, 所以其實求強連通分支和拓撲排序的思路有些相似, 先DFS(G), 並按post遞減的排序, 其實就是把分支(component)進行了拓撲排序, 如果我們能夠找到第一個強連通分支, 把它刪除, 再繼續往下一個個可以找出所有的強連通分支.
為什麽要按拓撲排序的順序找, 因為分支圖裏面post最大的那個分支, 只有出度無入度, 當取圖的轉置圖時, 就變成了沒有出度, 所以對轉置圖進行深度優先搜索不會找到其他分支的節點, 可以準確的找出屬於第一個強連通分支的所有節點. 所以上面算法中, 對轉置圖按post遞減進行深度優先搜索就可以按分支圖的拓撲順序找出所有強連通分支.
 1 def transpose(graph):
1 def transpose(graph):2 """
3 create transposed graph
4 """
5 t_graph = {}
6
7 for key, edges in graph.items():
8 for edge in edges:
9 if not t_graph.get(edge):
10 t_graph[edge] = [key]
11 else:
12 t_graph[edge].append(key)
13 #print t_graph
14 return t_graph
15 def SCC(graph):
16 """
17 Strongly_Connected_Components
18 """
19 global post
20 global pre
21 global clock
22 DFS(graph)
23 p = post.items()
24 p.sort(key=lambda x:x[1],reverse=True)
25 print p
26 t_graph = transpose(graph)
27 post = {}
28 pre = {}
29 clock = 1
30 for v,num in p:
31 if not pre.get(v):
32 print v, ‘==========================‘
33 visit(t_graph, v)

廣度和深度優先搜索的 區別
對於這兩種算法基本的目的都是要遍歷所有節點一次, 所以時間復雜度是一致的O(V+E)
兩者在實現上唯一的區別是, BFS使用Queue, 而DFS使用Stack, 這就是兩者所有區別的根源, Queue的先進先出特性確保了只有上一層的所有節點都被訪問過, 才會開始訪問下層節點, 從而保證了廣度優先, 而Stack的先進後出的特性, 會從葉節點不斷回溯, 從而達到深度優先.
兩者應用場景不同, BFS比較簡單, 主要用於求最短路徑, DFS復雜些, 主要用於graph decomposition, 即怎樣把一個圖分解成相互連通的子圖, 其中包含了有向圖的拓撲排序問題.
原文鏈接
基本數據結構(算法導論)與python

