day40 數據結構-算法(二)
阿新 • • 發佈:2017-11-17
圍墻 dea maxsize 由於 image closed images 哈希函數 鏈表 



什麽是數據結構?
- 簡單來說,數據結構就是設計數據以何種方式組織並存儲在計算機中。
- 比如:列表、集合與字典等都是一種數據結構。
- N.Wirth: “程序=數據結構+算法”
列表
- 列表:在其他編程語言中稱為“數組”,是一種基本的數據結構類型。
- 關於列表的問題:
- 列表中元素使如何存儲的?
- 列表提供了哪些基本的操作?
- 這些操作的時間復雜度是多少?
- 列表與可變對象*
棧
- 棧(Stack)是一個數據集合,可以理解為只能在一端進行插入或刪除操作的列表。
- 棧的特點:後進先出(last-in, first-out)
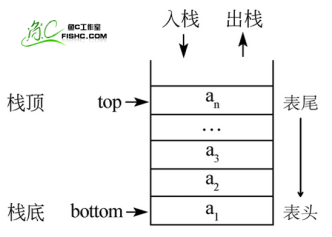
- 棧的概念:
- 棧頂
- 棧底
- 棧的基本操作:
- 進棧(壓棧):push
- 出棧:pop
- 取棧頂:gettop

棧的Python實現
- 不需要自己定義,使用列表結構即可。
- 進棧函數:append
- 出棧函數:pop
- 查看棧頂函數:li[-1]
棧的應用——括號匹配問題
- 括號匹配問題:給一個字符串,其中包含小括號、中括號、大括號,求該字符串中的括號是否匹配。
- 例如:
- ()()[]{} 匹配
- ([{()}]) 匹配
- []( 不匹配
- [(]) 不匹配
括號匹配問題——實現

1 def check_kuohao(s): 2 stack = [] 3 for char in s: 4 if char in {‘View Code(‘, ‘[‘, ‘{‘}: 5 stack.append(char) 6 elif char == ‘)‘: 7 if len(stack) > 0 and stack[-1] == ‘(‘: 8 stack.pop() 9 else: 10 return False 11 elif char == ‘]‘: 12 if len(stack) > 0 and stack[-1] == ‘[‘: 13 stack.pop() 14 else: 15 return False 16 elif char == ‘}‘: 17 if len(stack) > 0 and stack[-1] == ‘{‘: 18 stack.pop() 19 else: 20 return False 21 if len(stack) == 0: 22 return True 23 else: 24 return False
棧的應用——迷宮問題
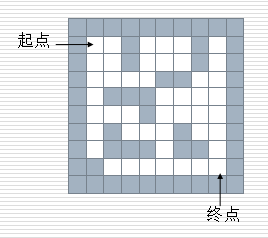
給一個二維列表,表示迷宮(0表示通道,1表示圍墻)。給出算法,求一條走出迷宮的路徑。
maze = [ [1,1,1,1,1,1,1,1,1,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,0,0,1,1,0,0,1],
[1,0,1,1,1,0,0,0,0,1],
[1,0,0,0,1,0,0,0,0,1],
[1,0,1,0,0,0,1,0,0,1],
[1,0,1,1,1,0,1,1,0,1],
[1,1,0,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,1]
]
解決思路
- 在一個迷宮節點(x,y)上,可以進行四個方向的探查:maze[x-1][y], maze[x+1][y], maze[x][y-1], maze[x][y+1]
- 思路:從一個節點開始,任意找下一個能走的點,當找不到能走的點時,退回上一個點尋找是否有其他方向的點。
- 方法:創建一個空棧,首先將入口位置進棧。當棧不空時循環:獲取棧頂元素,尋找下一個可走的相鄰方塊,如果找不到可走的相鄰方塊,說明當前位置是死胡同,進行回溯(就是講當前位置出棧,看前面的點是否還有別的出路)
迷宮問題——棧實現

1 dirs = [lambda x, y: (x + 1, y), lambda x, y: (x - 1, y), 2 lambda x, y: (x, y - 1), lambda x, y: (x, y + 1)] 3 def mgpath(x1, y1, x2, y2): 4 stack = [] 5 stack.append((x1, y1)) 6 while len(stack) > 0: # 棧不空時循環 7 curNode = stack[-1] # 查看棧頂元素 8 if curNode[0] == x2 and curNode[1]: 9 # 到達終點 10 for p in stack: 11 print(p) 12 break 13 for dir in dirs: 14 nextNode = dir(*curNode) 15 if mg[nextNode[0]][nextNode[1]] == 0: # 找到了下一個方塊 16 stack.append(nextNode) 17 mg[nextNode[0]][nextNode[1]] = -1 # 標記為已經走過,防止死循環 18 break 19 else: 20 mg[curNode[0]][curNode[1]] = -1 # 死路一條 21 stack.pop() 22 return FalseView Code
隊列
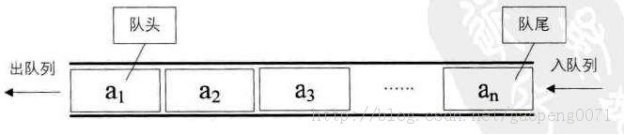
- 隊列(Queue)是一個數據集合,僅允許在列表的一端進行插入,另一端進行刪除。
- 進行插入的一端稱為隊尾(rear),插入動作稱為進隊或入隊
- 進行刪除的一端稱為隊頭(front),刪除動作稱為出隊
- 隊列的性質:先進先出(First-in, First-out)
- 雙向隊列:隊列的兩端都允許進行進隊和出隊操作。
隊列的實現
- 隊列能否簡單用列表實現?為什麽?
- 使用方法:from collections import deque
- 創建隊列:queue = deque(li)
- 進隊:append
- 出隊:popleft
- 雙向隊列隊首進隊:appendleft
- 雙向隊列隊尾進隊:pop
隊列的實現原理
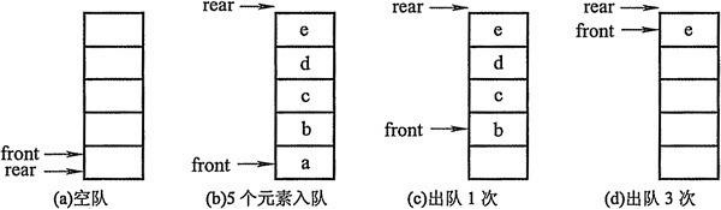
- 初步設想:列表+兩個下標指針
- 創建一個列表和兩個變量,front變量指向隊首,rear變量指向隊尾。初始時,front和rear都為0。
- 進隊操作:元素寫到li[rear]的位置,rear自增1。
- 出隊操作:返回li[front]的元素,front自減1。
- 這種實現的問題?
隊列的實現原理——環形隊列
- 改進方案:將列表首尾邏輯上連接起來。
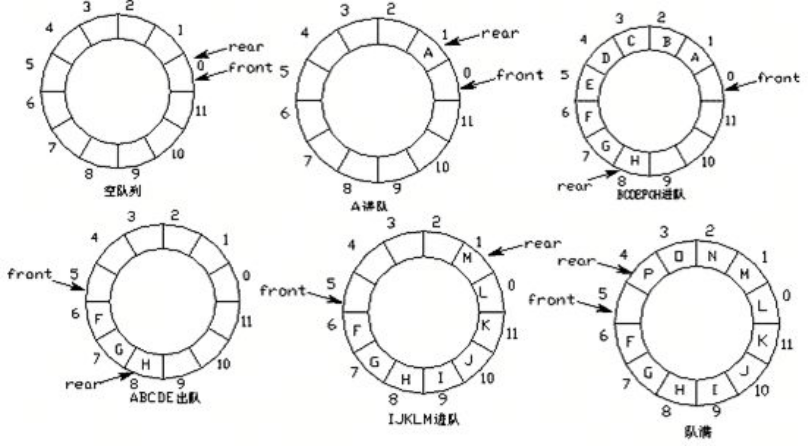
隊列的實現原理——環形隊列
- 環形隊列:當隊尾指針front == Maxsize + 1時,再前進一個位置就自動到0。
- 實現方式:求余數運算
- 隊首指針前進1:front = (front + 1) % MaxSize
- 隊尾指針前進1:rear = (rear + 1) % MaxSize
- 隊空條件:rear == front
- 隊滿條件:(rear + 1) % MaxSize == front
隊列的應用——迷宮問題
- 思路:從一個節點開始,尋找所有下面能繼續走的點。繼續尋找,直到找到出口。
- 方法:創建一個空隊列,將起點位置進隊。在隊列不為空時循環:出隊一次。如果當前位置為出口,則結束算法;否則找出當前方塊的4個相鄰方塊中可走的方塊,全部進隊。
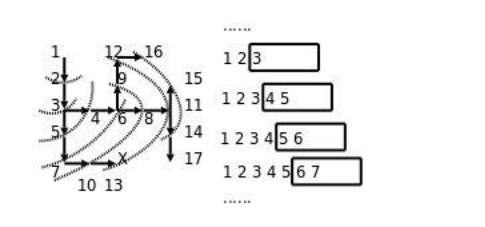
迷宮問題——隊列實現

1 def mgpath(x1, y1, x2, y2): 2 queue = deque() 3 path = [] 4 queue.append((x1, y1, -1)) 5 while len(queue) > 0: 6 curNode = queue.popleft() 7 path.append(curNode) 8 if curNode[0] == x2 and curNode[1] == y2: 9 #到達終點 10 print(path) 11 return True 12 for dir in dirs: 13 nextNode = dir(curNode[0], curNode[1]) 14 if mg[nextNode[0]][nextNode[1]] == 0: # 找到下一個方塊 15 queue.append((*nextNode, len(path) - 1)) 16 mg[nextNode[0]][nextNode[1]] = -1 # 標記為已經走過 17 return FalseView Code
鏈表
鏈表中每一個元素都是一個對象,每個對象稱為一個節點,包含有數據域key和指向下一個節點的指針next。通過各個節點之間的相互連接,最終串聯成一個鏈表。
節點定義:
class Node(object): def __init__(self, item): self.item = item self.next = None
頭結點

鏈表的遍歷
- 遍歷鏈表:
-

def traversal(head): curNode = head # 臨時用指針 while curNode is not None: print(curNode.data) curNode = curNode.next
View Code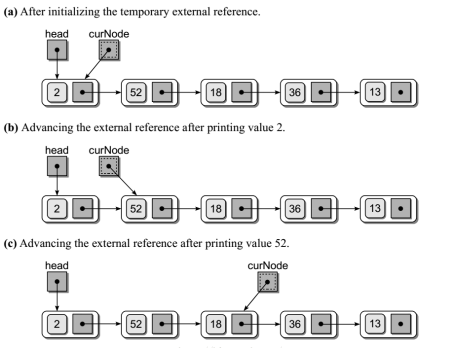
鏈表節點的插入和刪除
- 插入:
- p.next = curNode.next
- curNode.next = p
- 刪除:
- p = curNode.next
- curNode.next = curNode.next.next
- del p
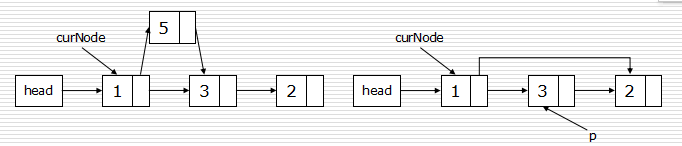
建立鏈表
- 頭插法:
-

1 def createLinkListF(li): 2 l = Node() 3 for num in li: 4 s = Node(num) 5 s.next = l.next 6 l.next = s 7 return l
View Code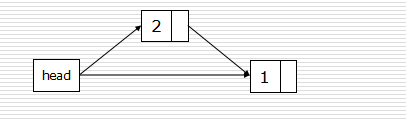
-
尾插法:
-

1 def createLinkListR(li): 2 l = Node() 3 r = l #r指向尾節點 4 for num in li: 5 s = Node(num) 6 r.next = s 7 r = s
View Code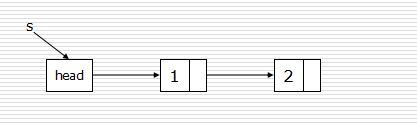
雙鏈表
雙鏈表中每個節點有兩個指針:一個指向後面節點、一個指向前面節點。
節點定義:

1 class Node(object): 2 def __init__(self, item=None): 3 self.item = item 4 self.next = None 5 self.prior = NoneView Code
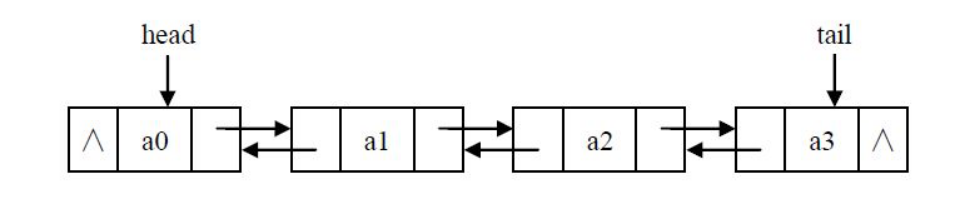
雙鏈表節點的插入和刪除
- 插入:
- p.next = curNode.next
- curNode.next.prior = p
- p.prior = curNode
- curNode.next = p
- 刪除:
- p = curNode.next
- curNode.next = p.next
- p.next.prior = curNode
- del p
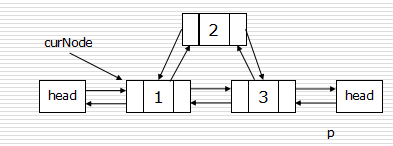
建立雙鏈表
- 尾插法:
-

1 def createLinkListR(li): 2 l = Node() 3 r = l 4 for num in li: 5 s = Node(num) 6 r.next = s 7 s.prior = r 8 r = s 9 return l, r
View Code
鏈表-分析
- 列表與鏈表
- 按元素值查找
- 按下標查找
- 在某元素後插入
- 刪除某元素
Python中的集合與字典(了解)
- 哈希表查找
- 哈希表(Hash Table,又稱為散列表),是一種線性表的存儲結構。通過把每個對象的關鍵字k作為自變量,通過一個哈希函數h(k),將k映射到下標h(k)處,並將該對象存儲在這個位置。
- 例如:數據集合{1,6,7,9},假設存在哈希函數h(x)使得h(1) = 0, h(6) = 2, h(7) = 4, h(9) = 5,那麽這個哈希表被存儲為[1,None, 6, None, 7, 9]。
- 當我們查找元素6所在的位置時,通過哈希函數h(x)獲得該元素所在的下標(h(6) = 2),因此在2位置即可找到該元素。
- 哈希函數種類有很多,這裏不做深入研究。
- 哈希沖突:由於哈希表的下標範圍是有限的,而元素關鍵字的值是接近無限的,因此可能會出現h(102) = 56, h(2003) = 56這種情況。此時,兩個元素映射到同一個下標處,造成哈希沖突。
解決哈希沖突:
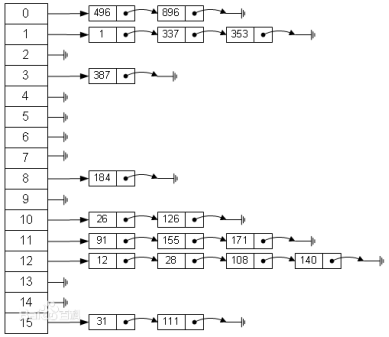
- 拉鏈法
- 將所有沖突的元素用鏈表連接
- 開放尋址法
- 通過哈希沖突函數得到新的地址
- 在Python中的字典: a = {‘name‘: ‘Alex‘, ‘age‘: 18, ‘gender‘: ‘Man‘}
- 使用哈希表存儲字典,通過哈希函數將字典的鍵映射為下標。假設h(‘name’) = 3, h(‘age’) = 1, h(‘gender’) = 4,則哈希表存儲為[None, 18, None, ’Alex’, ‘Man’]
- 在字典鍵值對數量不多的情況下,幾乎不會發生哈希沖突,此時查找一個元素的時間復雜度為O(1)。
day40 數據結構-算法(二)

