說明：本實例基於C語言編寫

一、進制轉換

　　1）、十進制轉其它進制

• 　　DEC轉BIN：N=25

　　(25)₂=11001

• 　　DEC轉OCT：N=125

　　(125)₈=175

• 　　DEC轉HEX：N=2581

　　(2581)₁₆=A15

　　2）、其它進制轉十進制

• 　　BIN轉DEC：(1100101)₂

　　(1100101)₂=1x2⁶+1x2⁵+0x2⁴+0x2³+1x2²+0x2¹+1x2⁰=64+32+0+0+4+0+1=101

• 　　OCT轉DEC：(2612)₈

　　(2612)₈=2x8³+6x8²+1x8¹+2x8⁰=1024+384+8+2=1418

• 　　HEX轉DEC：(A46C)₁₆

　　(A46C)₁₆=10x16³+4x16²+6x16¹+12x16⁰=40960+1024+96+12=42092

　　3）、二進制與八進制互轉

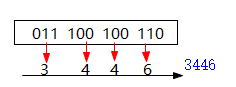
• 　　BIN轉OCT：(011100100110)₂

　　(011100100110)₂=(3446)₈

• 　　OCT轉BIN：(7514)₈

　　(7514)₈=(?111101001100?)₂

　　4）、二進制與十六進制互轉

• 　　BIN轉HEX：(0101001011)₂

　　(0101001011)₂=(14B)₁₆

• 　　HEX轉BIN：(B287)₁₆

　　(B287)₁₆=(?1011001010000111?)₂

　　5）、八進制與十六進制互轉

　　OCT轉HEX：OCT轉BIN轉HEX

　　HEX轉OCT：HEX轉BIN轉OCT

二、數字存儲

　　1）、無符號整數原碼存儲：N=126

　　2）、有符號正整數原碼存儲：N=126

　　參照上一個例子

　　3）、有符號負整數補碼存儲：-106

　　(106)₂=00000000000000000000000001101010

　　如果用4字節（32位來存儲）的話，(106)_補=11111111111111111111111110010110

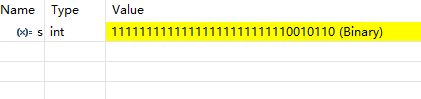
　　將補碼存儲的有符號負整數還原為十進制數

• 　　對補碼表示的數進行補碼運算得到這個十進制數的絕對值的二進制表示：01101010
• 將該二進制數轉換為十進制並添加符號(看最高位)即可：-10

　　補碼運算

　　4）、單精度浮點數存儲：余127碼

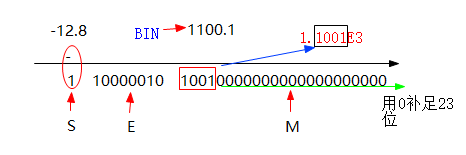
　　N = - 12.8（精度2位）

• 　　符號位S=1（負數）
• 　　轉化為二進制表示：(12.8)₂=(1100.1)₂，轉換為二進制的小數部分精度為1
• 　　規範化：(1.1001)x2³
• 　　指數E=3+127=130，二進制為：(130)₂=(10000010)₂
• 　　尾數M=(10010000000000000000000)₂
• 　　結果：1 10000010 10010000000000000000000

　　5）、雙精度浮點數存儲：余1023碼

　　操作方法和單精度浮點數的存儲一直，不同的是，雙精度浮點數的指數E用11位存儲，尾數用52位存儲。

進制轉換與數字存儲實例