下面根據我的理解一步一步引出信息熵及其公式的來源：

信息熵的公式

先拋出信息熵公式如下：

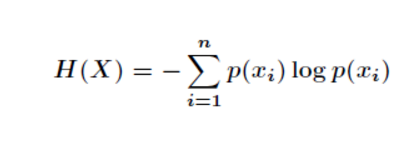
其中 代表隨機事件X為 的概率，下面來逐步介紹信息熵的公式來源！

信息量

信息量是對信息的度量，就跟時間的度量是秒一樣，當我們考慮一個離散的隨機變量x的時候，當我們觀察到的這個變量的一個具體值的時候，我們接收到了多少信息呢？

多少信息用信息量來衡量，我們接受到的信息量跟具體發生的事件有關。

信息的大小跟隨機事件的概率有關。越小概率的事情發生了產生的信息量越大，如湖南產生的地震了；越大概率的事情發生了產生的信息量越小，如太陽從東邊升起來了（肯定發生嘛，沒什麽信息量）。這很好理解！

例子

腦補一下我們日常的對話：

師兄走過來跟我說，立波啊，今天你們湖南發生大地震了。

我：啊，不可能吧，這麽重量級的新聞！湖南多低的概率發生地震啊！師兄，你告訴我的這件事，信息量巨大，我馬上打電話問問父母什麽情況。

又來了一個師妹：立波師兄，我發現了一個重要情報額，原來德川師兄有女朋友額~德川比師妹早進一年實驗室，全實驗室同學都知道了這件事。我大笑一聲：哈哈哈哈，這件事大家都知道了，一點含金量都沒有，下次八卦一些其它有價值的新聞吧！orz，逃~

因此一個具體事件的信息量應該是隨著其發生概率而遞減的，且不能為負。

但是這個表示信息量函數的形式怎麽找呢？

隨著概率增大而減少的函數形式太多了！不要著急，我們還有下面這條性質

如果我們有倆個不相關的事件x和y，那麽我們觀察到的倆個事件同時發生時獲得的信息應該等於觀察到的事件各自發生時獲得的信息之和，即：

h(x,y) = h(x) + h(y)

由於x，y是倆個不相關的事件，那麽滿足p(x,y) = p(x)*p(y).

根據上面推導，我們很容易看出h(x)一定與p(x)的對數有關（因為只有對數形式的真數相乘之後，能夠對應對數的相加形式，可以試試）。因此我們有信息量公式如下：

下面解決倆個疑問？

（1）為什麽有一個負號

其中，負號是為了確保信息一定是正數或者是0，總不能為負數吧！

（2）為什麽底數為2

這是因為，我們只需要信息量滿足低概率事件x對應於高的信息量。那麽對數的選擇是任意的。我們只是遵循信息論的普遍傳統，使用2作為對數的底！

信息熵

下面我們正式引出信息熵。

信息量度量的是一個具體事件發生了所帶來的信息，而熵則是在結果出來之前對可能產生的信息量的期望——考慮該隨機變量的所有可能取值，即所有可能發生事件所帶來的信息量的期望。即

轉換一下為：

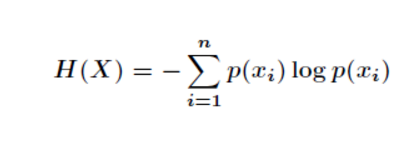
最終我們的公式來源推導完成了。

這裏我再說一個對信息熵的理解。信息熵還可以作為一個系統復雜程度的度量，如果系統越復雜，出現不同情況的種類越多，那麽他的信息熵是比較大的。

如果一個系統越簡單，出現情況種類很少（極端情況為1種情況，那麽對應概率為1，那麽對應的信息熵為0），此時的信息熵較小。

轉自：https://www.zhihu.com/question/22178202

信息熵公式的由來（轉）